30.Линейная зависимость, базис, вронскиан и связь между ними.

Определение 1. Система функций и называется линейно независимой на некотором интервале (a,b), если из системы равенств (3.2)

Следует, что В противном случае система функций и - линейно зависима на (a,b).

Определение 2. Определитель, составленный для системы функций и называется определителем Вронского и обозначается W(x). Итак . Теорема 1. Определитель Вронского для линейно независимой на интервале (a,b) системы решений и ЛОС ДУ не равен нулю ни в одной точке (a,b). Доказательство. Докажем теорему методом от противного. Предположим, что существует точка , в которой

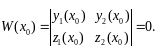Составим линейную однородную систему уравнений с неизвестными  и  : (3.3)

Так как определитель системы (3.3) равен нулю, то система имеет бесконечное множество ненулевых решений. Пусть - одно из них. С помощью этих констант и двух линейно независимых на (a,b) решений системы (3.1) и составим две функции (3.4) Согласно следствию из свойств решений ЛОС ДУ функции (3.4) являются решениями системы (3.1), которые в силу (3.3) в точке обращаются в нуль. Следовательно, y(x), z(x) – решение следующей задачи Коши: Но таким решением может быть только нулевое решение: y(x)=0, z(x)=0 при , т.е.

Причем . Это означает, что система функций и линейно зависима на (a,b), что противоречит условию теоремы. Значит наше предположение о существовании на (a,b) точки , в которой , неверно, что и доказывает теорему. Определение 2. Линейно независимые на (a,b) решения ЛОС ДУ и называются фундаментальной системой решений системы (3.1). Теорема 2. Если семейство функций и образует фундаментальную систему решений ЛОС ДУ (3.1), то их линейная комбинация , (3.5)

где - произвольные постоянные, дает общее решение системы (3.1) Доказательство.

3. Выражение (3.5), согласно следствию из свойств решений ЛОС ДУ, является решением системы уравнений (3.1).

4. Докажем, что (3.5) – общее решение (3.1), т.е. докажем, что каковы бы ни были начальные условия задачи Коши , всегда найдутся значения постоянных такие, что выделенное из общего частное решение ЛОС ДУ:

будет удовлетворять этим условиям. Для этого подставим в (3.5) начальные условия: (3.6)

Определителем этой алгебраической системы линейных уравнений является определитель Вронского : ,

который, согласно теореме 1, не равен нулю. Следовательно, система уравнений (3.6) имеет решение и притом единственное.

31. Формула Лиувилля для линейной системы. Фундаментальная матрица. Построение общего решения.

Фундаментальная система решений и фундаментальная матрица

Вектор-функции x₁(t), x₂(t), ..., x_n(t) являются линейно зависимыми на интервале [a, b], если найдутся такие числа c₁, c₂, ..., c_n, одновременно не равные нулю, что выполняется тождество

Если указанное тождество выполняется лишь при условии то вектор-функции x_i (t) называются линейно независимыми на заданном интервале.  Любая система n линейно независимых решений x₁(t), x₂(t), ..., x_n(t) называется фундаментальной системой решений.  Квадратная матрица Φ(t), столбцы которой образованы линейно независимыми решениямиx₁(t), x₂(t), ..., x_n(t), называется фундаментальной матрицей системы уравнений. Она имеет следующий вид:

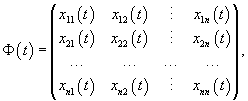
где x_ij (t) − координаты линейно независимых векторных решений x₁(t), x₂(t), ..., x_n(t).  Заметим, что фундаментальная матрица Φ(t) является невырожденной, т.е. для нее всегда существует обратная матрица Φ ⁻¹(t). Поскольку фундаментальная матрица содержит n линейно независимых решений, то при ее подстановке в однородную систему уравнений получаем тождество

Умножим это уравнение справа на обратную функцию Φ ⁻¹(t):

Полученное соотношение однозначно определяет однородную систему уравнений, если задана фундаментальная матрица.  Общее решение однородной системы выражается через фундаментальную матрицу в виде

где C − n-мерный вектор, состоящий из произвольных чисел.  Определитель фундаментальной матрицы Φ(t) называется определителем Вронского или вронскианом системы решений x₁(t), x₂(t), ..., x_n(t):

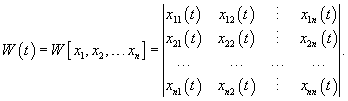
Определитель Вронского удобно использовать для проверки линейной независимости решений. Справедливы следующие правила:

• Решения x₁(t), x₂(t), ..., x_n(t) однородной системы уравнений являются фундаментальной системойтогда и только тогда, когда соответствующий вронскиан отличен от нуля в какой-нибудь точке tинтервала [a, b].

• Решения x₁(t), x₂(t), ..., x_n(t) являются линейно зависимыми на интервале [a, b] тогда и только тогда, когда вронскиан тождественно равен нулю на этом интервале. Для определителя Вронского системы решений x₁(t), x₂(t), ..., x_n(t) справедлива формула Лиувилля-Остроградского:

где tr (A(τ)) − след матрицы A(τ), т.е. сумма всех диагональных элементов:

Формула Лиувилля-Остроградского может применяться для построения общего решения однородной системы, если известно одно частное решение этой системы.

Определение 4. Общим решением линейной системы уравнений (2) называется множество всех решений этой системы. Теорема 8. Пусть 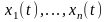- фундаментальная система решений однородной системы уравнений (3), тогда формула (15)

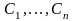где - произвольные постоянные, дает общее решение этой системы. Множество всех решений однородной системы уравнений (3) образует _n-мерное векторное пространство, базисом которого может служить любая фундаментальная система решений.