24.Понятие нормальной системы. Теорема существования и единственности решения задачи Коши для нормальной системы. Схема доказательства.

Нормальные системы обыкновенных дифференциальных уравнений.

Определение. Совокупность соотношений вида:

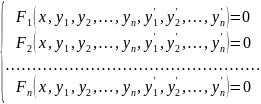
где х- независимая переменная, у1, у2,…,уn – искомые функции, называется системой дифференциальных уравнений первого порядка.

Определение. Система дифференциальных уравнений первого порядка, разрешенных относительно производных от неизвестных функций называется нормальной системой дифференциальных уравнений.

Такая система имеет вид: 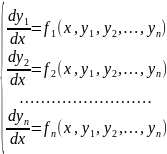(1)

Для примера можно сказать, что график решения системы двух дифференциальных уравнений представляет собой интегральную кривую в трехмерном пространстве.

Нормальная система в векторных обозначениях примет вид

где  .

Определение. Вектор-функция   называется решением нормальной системы (1) на промежутке  , если:

1.

2.

3.

Рассмотрим начальное условие

Точка (x0,y0) называется начальной точкой, а ее координаты x0,y0 называются начальными данными.

Определение. Задача нахождения решения нормальной системы (1), удовлетворяющего начальному условию (2), называется задачей Коши.

Система уравнений вида

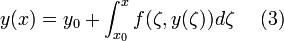
где  , называется системой интегральных уравнений.

Вектор-функция   называется решением на промежутке   системы (3), если:

1.

2.

3.

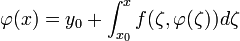
Лемма об эквивалентности. Вектор-функция   - решение задачи Коши (1) при условии (2) тогда и только тогда, когда   решение системы интегральных уравнений (3).

Теорема существования и единственности решения задачи Коши.

Пусть вектор-функция   удовлетворяет на каждом компакте области G условию Липшица

Тогда:

1) найдется такое δ > 0, что при | x − x0 | решение задачи Коши (1) при условии (2) существует,

2)решение задачи Коши единственно

В силу леммы об эквивалентности доказательство теоремы сводится к доказательству существования и единственности решения системы интегральных уравнений (3).

A)Существование

Поскольку   и G - открытое множество, то   что замкнутый цилиндр   принадлежит G. В силу того, что цилиндр Gpq компакт то

Будем строить решение системы интегральных уравнений (3) методом приближений Пикара при | x0 − x | < δ, где  . Определим последовательные приближения следующим рекурентным образом при  :

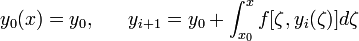
ясно, что каждая yi(x) непрерывна при (x,y), и что 

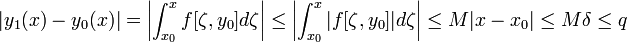
Как известно из курса анализа, равномерная сходимость функционального ряда   эквивалентна равномерной сходимости ряда вида

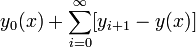
докажем оценку

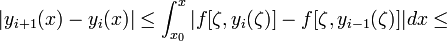
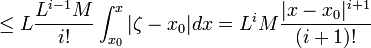
По теореме Вейршрасса получем, что

И

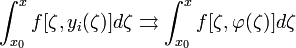
Единственность следует из леммы Гронуолла.

25. Интегралы нормальной системы и их свойства.

Нормальной системой дифференциальных уравнений называется система вида 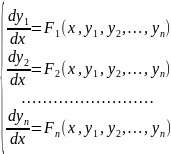(1)

Где 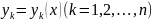— искомые функции независимой переменной х,

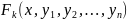— заданные функции указанных аргументов. Порядком нормальной системы называется число входящих в нее уравнений. Решением системы

(1) в интервале (a,b) называется совокупность n функций 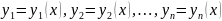, определенных и непрерывно дифференцируемых в этом интервале, если она обращает в тождество каждое из уравнений данной системы:

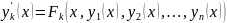
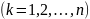
Для всех xϵ(a,b).

Задачи Коши для системы (1). Найти решение

,

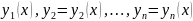Где 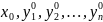- заданные числа.

Совокупность n функций 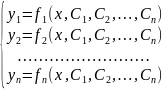(2)

Называется общим решением системы (1), если:

1)  система (2) разрешима относительно произвольных постоянных 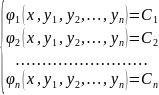(27.23)

2)  совокупность функций (2) является решением системы (1) при всех значениях постоянных 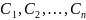, определяемых формулами (27.23).

Решение, получающееся из общего решения при фиксированных значениях произвольных постоянных, называется частным.

Каждое из равенств (27.23), т. е.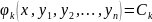 (k=1,2,…,n),

называется первым интегралом системы (1), а каждая из функций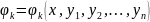  — интегралом этой системы. Совокупность первых интегралов называется общим интегралом системы (1).

Первые интегралы (27.23), образующие общий интеграл системы (1), обладают тем свойством, что интегралы 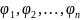независимы, т. е. между функциями не существует соотношения вида Ф( )=0 ни при каком выборе функции Ф.

При некоторых условиях, наложенных на правые части уравнений системы

(1), эта система имеет n независимых интегралов.

Перепишем систему (1) так:

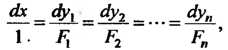(27.24)

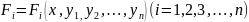
Система (27.24) дифференциальных уравнений первого порядка называется системой в симметрической форме, соответствующей нормальной системе (1).

Это частный случай системы в симметрической форме общего вида: .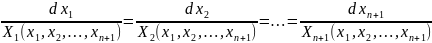

Если дана система дифференциальных уравнений в симметрической форме,

то, принимая 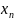за независимую переменную, ее можно привести к следующей нормальной системе (n-1)-го порядка:

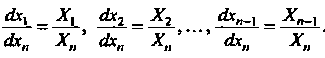(27.26) Решение, интеграл, первый интеграл, общее решение и общий интеграл системы (27.26) называют соответственно решением, интегралом, первым интегралом, общим решением и общим интегралом системы (27.25).

26. Интегрирование нормальной системы сведением к одному уравнению. Частным случаем канонической системы дифференциальных уравнений является одно уравнение n-го порядка, разрешенное относительно старшей производной.

Введением новых функций

э то уравнение заменяется нормальной системой n уравнений

…………….

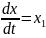
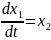
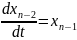
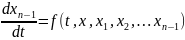
Можно утверждать и обратное, что, вообще говоря, нормальная система n уравнений первого порядка

……………………………………………

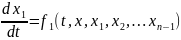
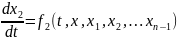
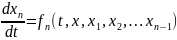
эквивалентна одному уравнению порядка n. На этом основан один из методов интегрирования систем дифференциальных уравнений — метод исключения. Проиллюстрируем этот метод на примере системы двух уравнений:

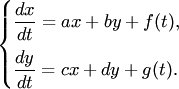
Здесь a,b,c,d — постоянные коэффициенты, а f(y) и g(t) — заданные функции; x(t) и y(t) — искомые функции. Из первого уравнения системы (1) находим

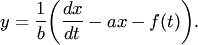
Подставляя во второе уравнение системы вместо у правую часть (2), а вместо 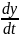  производную от правой части (2), получаем уравнение at второго порядка относительно x(t)

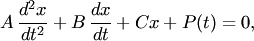
где A,B,C — постоянные. Отсюда находим x=x(t,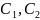 ). Подставив найденное выражение для x и   в (2), найдем y.