23.Решение с помощью рядов.

Решение дифференциальных уравнений с помощью

степенных рядов.

С помощью степенных рядов возможно интегрировать дифференциальные уравнения.

Рассмотрим линейное дифференциальное уравнение вида:

y⁽ⁿ⁾ + p₁(x)y^(n-1) + p₁(x)y^(n-2) + …+p_n(x)y = f(x)

Если все коэффициенты и правая часть этого уравнения разлагаются в сходящиеся в некотором интервале степенные ряды, то существует решение этого уравнения в некоторой малой окрестности нулевой точки, удовлетворяющее начальным условиям.

Это решение можно представить степенным рядом: y = c₀ + c₁x + c₂x² + c₃x³ +…

Для нахождения решения остается определить неизвестные постоянные ci.

Эта задача решается методом сравнения неопределенных коэффициентов. Записанное выражение для искомой функции подставляем в исходное дифференциальное уравнение, выполняя при этом все необходимые действия со степенными рядами (дифференцирование, сложение, вычитание, умножение и пр.)

Затем приравниваем коэффициенты при одинаковых степенях х в левой и правой частях уравнения. В результате с учетом начальных условий получим систему уравнений, из которой последовательно определяем коэффициенты ci.

Отметим, что этот метод применим и к нелинейным дифференциальным уравнениям.

Пример. Найти решение уравнения = 0 с начальными условиями y(0)=1, 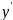(0) = 0.

Решение уравнения будем искать в виде y = c₀ + c₁x + c₂x² +…

= c₁ +2c₂x + 3c₃x² + 4c₄x³ + …

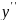= 2c₂ + 6c₃x + 12c₄x² + 20c₅x³ +…

Подставляем полученные выражения в исходное уравнение:

(2c₂ + 6c₃x + 12c₄x² + 20c₅x³+…) – (c₀x + c₁x² + c₂x³ + c₃x⁴…) = 0

2c₂ + x(6c₃ - c₀) + x² (12c₄ – c₁) + x³(20c₅ – c₂) + x⁴(30c₆ – c₃) + … = 0

Отсюда получаем: 2c₂ = 0

6c₃ - c₀ = 0

12c₄ – c₁ = 0

20c₅ – c₂ = 0

30c₆ – c₃ = 0

…………….

Получаем, подставив начальные условия в выражения для искомой функции и ее первой производной: c₀ = 1, c₁ = 0.

Окончательно получим: c₀ = 1, c₁ = 0, c₂ = 0, c₃ = 1/6, c₄ = 0, c₅ = 0, c₆ = 1/180, ….

Итого: y = 1 + x³/6 + x⁶/180 + …

Существует и другой метод решения дифференциальных уравнений с помощью рядов. Он носит название метод последовательного дифференцирования.

Рассмотрим тот же пример. Решение дифференциального уравнения будем искать в виде разложения неизвестной функции в ряд Маклорена.

y = y(0) +

Если заданные начальные условия y(0) = 1, (0) = 0 подставить в исходное дифференциальное уравнение, получим, что (0) = 0. Далее запишем дифференциальное уравнение в виде и будем последовательно дифференцировать его по х.

………………………………………………………

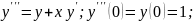
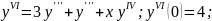
После подстановки полученных значений получаем:

y = 1 + x³/6 + x⁶/180 + … Решение дифференциальных уравнений с помощью рядов Тейлора Предположим, что требуется найти решение y(x)задачи Коши для дифференциального уравнения второго порядка

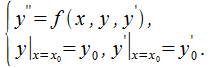   Находим в виде ряда Тейлора:

(30.14)

Значения определены, следовательно сразу можно найти Чтобы вычислить следующие коэффициенты ряда (30.14) требуется последовательное использование производных от , далее необходимо подставить их определенные уже значения предыдущих производных. Пример: Записать первые три члена разложения в с.р. решения задачи Коши

находим в следующем виде

 

Получаем:

Итак,   Обозначенный метод используется для приближенного решения уравнений любого порядка.