12)Задача Коши для уравнения го порядка. Теорема существования и единственности решения. Обыкновенным дифференциальным уравнением n –го порядка называется уравнение вида

F (x, y(x), y '(x), y ''(x),  …  , y⁽ⁿ⁾(x)) = 0,

где F — известная функция (n + 2)-х переменных, x — независимая переменная из интервала (a,b), y(x) — неизвестная функция. Число nназывается порядком уравнения. 

Функция y(x) называется решением (или интегралом) дифференциального уравнения на промежутке (a, b), если она n раз дифференцируема на (a, b) и при подстановке в уравнение обращает его в тождество.

Обыкновенные дифференциальные уравнения, разрешенные относительно старшей производной, называют уравнениями в нормальной форме:

y⁽ⁿ⁾ = f(x, y, y ',  y '',  …  , y^{(n − 1)}).

Дифференциальное уравнение обычно имеет бесконечно много решений. Чтобы выделить нужное решение, используют дополнительные условия. 

Чтобы выделить единственное решение уравнения n–го порядка обычно задают n начальных условий y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1}.

 Задачей Коши (или начальной задачей) называется задача отыскания решения y = y(x) уравнения

F(x, y(x), y '(x), y ''(x),  …  , y^(n )(x)) = 0,    x>x₀,

удовлетворяющего условиям

y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1}.

 Условия   y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1} называются начальными данными, начальными условиями или данными Коши.

 Любое конкретное решение y = φ(x) уравнения n –го порядка F(x, y(x), y '(x), y ''(x),  …  , y^(n )(x)) = 0, называется частным решением.

 Общим решением дифференциального уравнения

F(x, y(x), y '(x), y ''(x),  …  , y^(n )(x)) = 0

называется функция

y = Ф(x,  С₁, С₂, … , С_n),

содержащая некоторые постоянные (параметры) С₁, С₂, … , С_n, и обладающая следующими свойствами:

1.Ф(x, С₁, С₂,  … , С_n) является решением уравнения при любых допустимых значениях С₁, С₂, … , С_m;

2. для любых начальных данных  y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1}, для которых задача Коши имеет единственное решение,

существуют значения постоянных С₁ = A₁, С₂ = A₂,  … , С_n = A_n, такие что решение y = Ф(x, A₁, A₂,  …, A_n) удовлетворяет заданным начальным условиям.

Иногда частное или общее решение уравнения удается найти только в неявной форме: f(x, y) = 0 или G(x, y, С₁,  С₂,  ..., С_n) = 0.

Такие неявно заданные решения называются частным интегралом или общим интегралом уравнения.

Теорема существования и единственности решения для уравнения n-ого порядка.

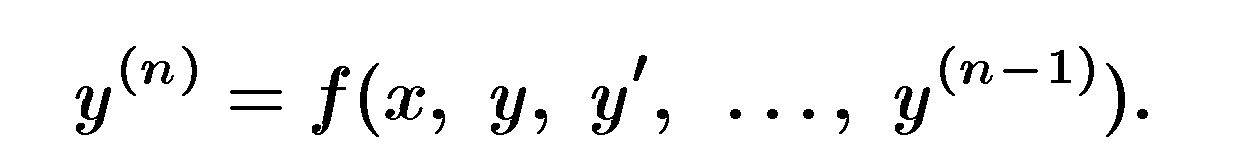
13)Уравнения высших порядков, допускающих понижение порядка.

–общая запись ДУ n-ого порядка.

14)Общие свойства решений линейного дифференциального уравнения. Теорема существования и единственности решения задачи Коши.

Рассмотрим линейное дифференциальное уравнение n –го порядка

y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = f(x).

с непрерывными коэффициентами a_n-1(x), a_n-2(x), ..., a₁(x), a₀(x) и непрерывной правой частью f(x).

Свойства решений линейных дифференциальных уравнений.

1. Если y₁(x) и y₂(x)— два решения линейного однородного дифференциального уравнения

y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = 0

то любая их линейная комбинация y(x) = C₁y₁(x) + C₂y₂(x) является решением этого однородного уравнения.

2. Если y₁(x) и y₂(x) — два решения линейного неоднородного уравнения L(y) = f(x) , то их разность y(x) = y₁(x) − y₂ (x) является решением однородного уравнения L(y) = 0 . 

3. Любое решение неоднородного линейного уравнения L(y) = f(x) есть сумма любого фиксированного (частного) решения неоднородного уравнения и некоторого решения однородного уравнения. 

4. Если y₁(x) и y₂(x) — решения линейных неоднородных уравнений L(y) = f₁(x) и L(y) = f₂(x) соответственно, то их сумма y(x) = y₁(x) +y₂(x) является решением неоднородного уравнения L(y) = f₁(x) + f₂(x).

Теорема существования и единственности решения задачи Коши.

Пусть функция f(x, y) и ее частная производная   f_y(x, y)  непрерывны в некоторой области D плоскости x0y и точка (x₀, y₀) принадлежит областиD.

Тогда :

— в некоторой окрестности (x₀ − δ, x₀ + δ) точки x₀ существует решение задачи Коши  

— если y = φ₁(x) и y = φ₂(x) два решения задачи Коши, то φ₁(x) = φ₂(x) на (x₀ − δ, x₀ + δ) .

Геометрически это означает, что если условия теоремы выполнены, то через каждую точку (x₀, y₀) области D проходит единственнаяинтегральная кривая уравнения.

Бесконечное множество решений уравнения  

можно рассматривать как однопараметрическое семейство функций y = φ(x; x₀) — семейство решений задачи Коши  

элементы которого различны для разных значений x₀ . Иными словами область D "расслаивается" на интегральные кривые y = φ(x; x₀) . 

Важно понимать, что результат теоремы имеет локальный характер — существование и единственность решения гарантированы, вообще говоря, только в малой окрестности точки x₀ . Важно также понимать, что условия теоремы существования и единственности достаточные условия. Нарушение условий теоремы не означает, что решение задачи не существует либо что оно не единственно.

15)Линейные однородные дифференциальные уравнения. Свойства решений. Линейная зависимость и независимость решений. Определитель Вронского. Критерий независимости решений.

Рассмотрим на [a; b] линейное однородное дифференциальное уравнение

y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = 0.

Общим решением этого уравнения на отрезке [a;b] называется функция y = Φ(x, C₁,..., C_n ), зависящая от n произвольных постоянных C₁,..., C_n и удовлетворяющая следующим условиям :

− при любых допустимых значениях постоянных C₁,..., C_n функция y = Φ(x, C₁,..., C_n ) является решением уравнения на [a; b] ;

− какова бы ни была начальная точка (x₀, y₀, y_1,0 ,..., y_{n − 1,0} ) , x₀∈ [a;b] , существуют такие значения C₁ =C₁₀ , ..., C_n = C_n0 , что функция y = Φ(x,C₁₀ , ..., C_n0) удовлетворяет начальным условиям y(x₀) = y₀, y '(x₀) = y_1,0 ,..., y^{(n − 1)} (x₀) = y_{n− 1,0} .

Справедливо следующее утверждение ( теорема о структуре общего решения линейного однородного уравнения).

Если все коэффициенты уравнения линейного однородного дифференциального уравнениния непрерывны на отрезке [a;b] , а функции y₁(x),y₂(x),..., y_n(x) образуют фундаментальную систему решений этого уравнения, то общее решение уравнения имеет вид

y(x,C₁,..., C_n) = C₁ y₁(x) + C₂ y₂(x) + ... + C_n y_n(x),

где C₁,...,C_n — произвольные постоянные.

Определитель Вронского

Определителем Вронского W(x; y₁(x), y₂(x), ..., y_n(x)) называется определитель, первая строка которого образована функциями y₁(x), y₂(x), ..., y_n(x) из C_n-1[a, b] , а последующие строки образованы производными от функций предыдущей строки:

Рассмотрим линейное однородное дифференциальное уравнение

y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = 0.

Справедливо следующее необходимое и достаточное условие линейной независимости решений этого уравнения.

Решения y₁(x), y₂(x), ..., y_n(x) линейного однородного дифференциального уравнения линейно независимы на отрезке [a; b] тогда и только тогда, когда определитель Вронского этих функций W(x ; y₁(x), y₂(x), ..., y_n(x)) не обращается в нуль ни в одной точке отрезка [a; b] .

 

Для определителя Вронского W(x ; y₁(x), y₂(x), ..., y_n(x)) решений y₁(x), y₂(x), ..., y_n(x) линейного однородного дифференциального уравнения с непрерывными на [a; b] коэффициентами, справедлива формула Остроградского–Лиувилля:

Из формулы Остроградского-Лиувилля, в частности, следует:

− если W(x₀ ; y₁(x), y₂(x), ..., y_n(x)) = 0, x₀∈[a, b], то W(x; y₁(x), y₂(x), ..., y_n(x)) ≡ 0 на [a, b];

− если же W(x₀ ; y₁(x), y₂(x), ..., y_n(x)) ≠ 0, x₀∈[a, b], то W(x; y₁(x), y₂(x), ..., y_n(x)) ≠0 на [a, b].