4. Атом водорода

Атом водорода – связанная система, состоящая из положительно заряженного ядра – протона– и отрицательного заряженного электрона. Размеры атома определяются размерами его электронной оболочки. Характерные размеры атомов 10^-8 см. Потенциальная энергия связи электрона с протоном определяется кулоновским взаимодействием (протон предполагается покоящимся) и равна e²/r, где r расстояние между протоном и электроном. В этом случае уравнение Шрёдингера для стационарного состояния (волновая функция не зависит от времени) принимает вид:

. (2.11)

Возможные значения стационарных состояний электрона получаются при решении уравнения (2.11) с потенциалом U(r)=e²/r и определяются соотношением

(2.12)

где N –главное квантовое число, определяющее энергии различных состояний в атоме водорода (N=1,2,3…) см. рис. 2.1, а R – постоянная Ридберга (1,097410⁵ см^-1).

Волновая функция, описывающая стационарные состояния атома водорода, имеет стандартный вид

(2.13)

где радиальная функция R_nl(r) и угловая функция Y_lm(,) удовлетворяют уравнениям

(2.14)

(2.15)

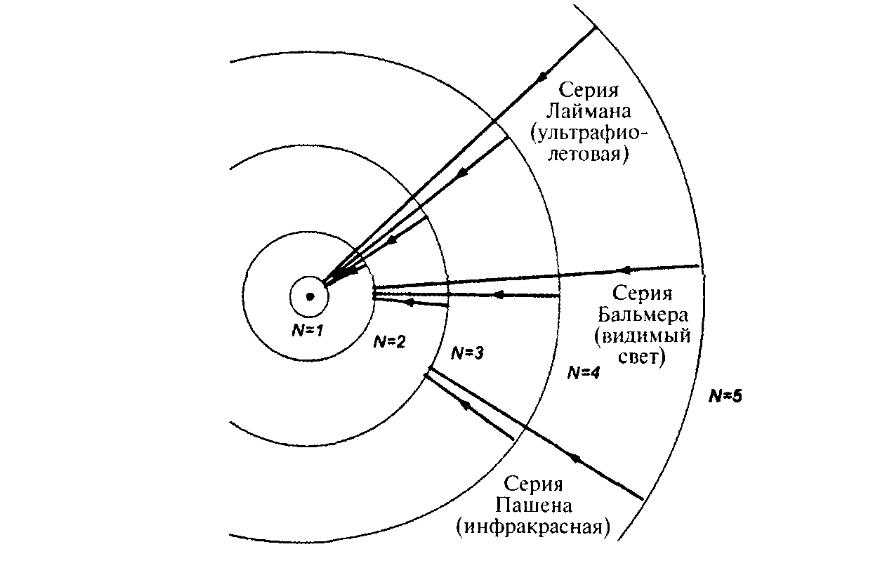
Рис. 2.1. Орбиты модели атома Бора.

Состояния атома водорода описываются радиальным, орбитальным и магнитным квантовыми числами n, l, и m. Важно отметить, что между главным квантовым числом N, используемым в атомной спектроскопии, и квантовыми числами n и l существует следующая связь:

N=n+l. (2.16)

Квантовые числа n, l и m полностью характеризуют состояние электрона в атоме водорода в рассмотренной выше упрощенной модели. Состояние с N=1 называется основным состоянием атома водорода, так как в этом состоянии обладает наименьшей энергией. Состояния с N=2, 3, … называются возбуждёнными состояниями. Энергия возбуждения Е_возб (энергия, которую необходимо сообщить системе, чтобы она перешла из начального состояния N_i в конечное состояние N_f) определяется из соотношения

(2.17)

Все состояния от N=1 до N= являются связанными состояниями, так как имеют отрицательные энергии. При приближении N к бесконечности энергии соседних состояний сближаются, и разница в энергиях этих состояний становится настолько мала, что расщеплённые уровни сливаются, и дискретный спектр уровней трансформируется в непрерывный (сплошной). Когда энергия электрона становится положительной (Е0), система превращается в несвязанную, и электрон становится свободным.

Важной особенностью любой сферически симметричной системы является совпадение энергий состояний. Это явление носит название вырождения. В любом центральном потенциале энергия не зависит от числа m. Поскольку m=0, 1, 2, 3,…l, то для каждого орбитального момента l имеется 2l+1 значений m, и все эти значения отвечают одной и той же энергии. Таким образом, число различных (в данном случае по m) квантовых уровней с совпадающей энергией, т. е. кратность вырождения, также равно 2l+1.Это минимально возможная кратность вырождения, присущая центральному полю. Обычно возникает дополнительное вырождение, обусловленное определёнными комбинациями n и l. Рассмотрим эту ситуацию для кулоновского потенциала.

В этом потенциале энергия определяется только главным квантовым числом N=n+l. Каждому уровню с главным кантовым числом N соответствует N состояний, различающихся квантовыми числами l=0, 1, 2,…, N-1. Такое вырождение характерно только для кулоновского поля. Кроме того, каждое из этих вырожденных по l состояний (2l+1)- кратно вырождено по числу m. Таким образом, полная кратность вырождения стационарного состояния с главным квантовым числом N даётся выражением

.

5. Спин

Спин -собственный момент количества движения частицы. Спин был первоначально введён для того, чтобы объяснить экспериментально наблюдаемый факт – расщепление спектральных линий на две близко расположенные компоненты. Между значением вектора спина и квантовым числом спина s имеется такое же соответствие, как между значением вектора орбитального момента и орбитальным квантовым числом l, а именно:

В отличие от орбитального квантового числа l , которое может быть лишь целым числом или нулём, спиновое квантовое число s может быть как целым (включая нуль), так и полуцелым (1/2, 3/2, 5/2,…), но при этом для каждой элементарной частицы он может принимать единственное присущее этому типу частиц значение. Так, спины  -мезона и К –мезона равны 0. Спины электрона, протона, нейтрино, кварков и их античастиц равны ½. Спин фотона равен 1. Спин частицы невозможно изменить, так же как её заряд или массу. Это её неизменная квантовая характеристика

Как и в случае других квантовых векторов, проекция вектора спина s_z на любое фиксированное направление в пространстве (например, ось z) может принимать 2s+1 значение. Исключение составляют спины частиц с собственной массой, равной 0. В этом случае существует лишь две проекции спина на ось направления движения.

Максимальная величина квантового числа проекции спина s_z совпадает с S . Так как спин электрона равен ½, то проекция этого спина может принимать лишь два значения s_z=1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если проекция -1/2, то говорят, что спин направлен вниз.

Если вероятности различных направлений спина одинаковы (спины частиц ориентированы произвольно), то говорят о равной нулю поляризации частиц. Если спины направлены в одну сторону, то говорят о единичной (или стопроцентной) поляризации. Если спин направлен перпендикулярно импульсу частицы, то говорят о поперечной поляризации. Продольная (круговая) поляризация означает, что спин частицы направлен вдоль её импульса.

В зависимости от того, как направлен спин относительно импульса при продольной поляризации, различают правую и левую поляризацию. Правополяризованной считается частица, спин которой направлен по импульсу, левополяризованной – против импульса. Для характеристики взаимного направления спина и импульса частицы используют понятие спиральности (см. рис. 2.2). Спиральностью h называют величину

. (2.18)

Правополяризованная частица имеет положительную спиральность (h=+1), левополяризованная –отрицательную (h = -1).

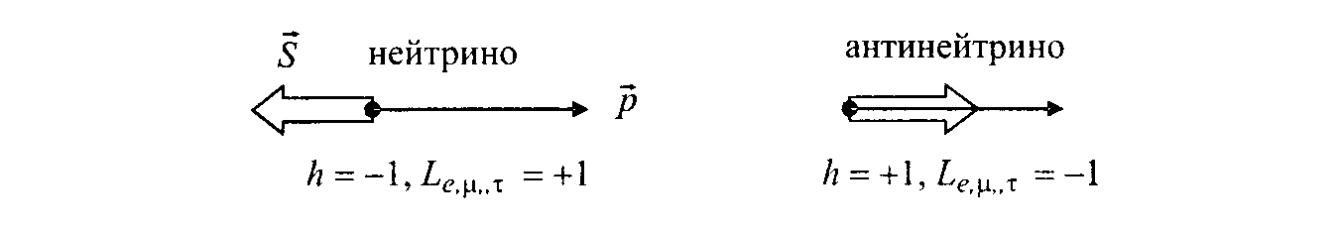
Рис. 2.2. Спиральности нейтрино и антинейтрино. Нейтрино – левополяризованная частица, антинейтрино – правополяризованная частица.