3. Кинематика ядерных реакций.

Рассмотрим реакцию A(a,bcd)B.

Запишем закон сохранения энергии через массы и кинетические энергии Т

(T_A+T_a)+ (M_A+m_a)c²=(T_B+T_b+T_c+T_d)+ (M_B+m_b+m_c+m_d)c². Определим энергию реакции как

Q=(M_A+m_a)c²-(M_B+m_b+m_c+m_d)c².

Тогда закон сохранения энергии запишется в виде

(T_A+T_a) =(T_B+T_b+T_c+T_d)- Q

При Q0 (экзотермическая реакция) процесс идёт при любом значении (T_A+ T_a).

При Q<0 (эндотермическая) реакция идёт лишь при определённых пороговых значениях кинетической энергии во входном канале.

Порог реакции- это минимальная суммарная кинетическая энергия сталкивающихся частиц и ядер, при которой реакция, идущая с поглощением энергии становится возможной.

(8.1)

Системы координат:

Л.С.К.-(лабораторная система координат) – система координат, связанная с наблюдателем. Обычно в этой системе мы имеем движущийся снаряд (частицу) и покоящуюся мишень ядро.

С.Ц.М.-(система центра масс) система, в которой суммарный импульс взаимодействующих частиц равен нулю.

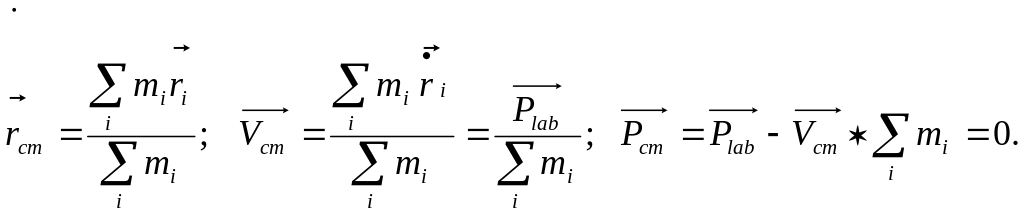
Ограничимся двумя частицами во входном канале. В этом случае функция Лагранжа такой системы имеет вид:

. (8.2)

Назовем r = r₁-r₂ вектором взаимного расстояния и поместим начало координат в центре инерции, что даёт: 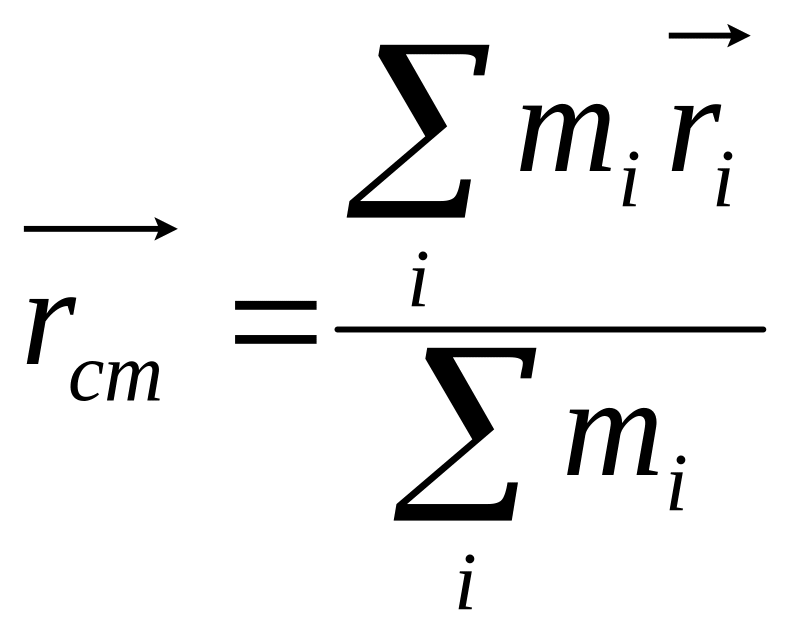=0. Откуда получаем:

.

Подставляя эти выражения в уравнение (8.2) для функции Лагранжа, получаем:

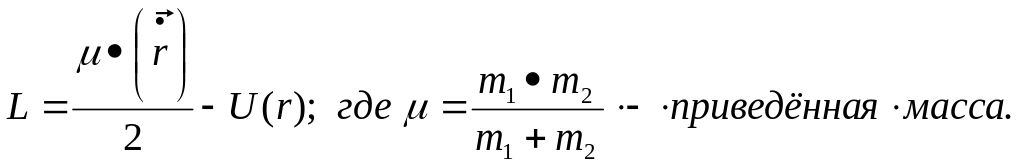
Выше приведённая функция Лагранжа формально совпадает с подобной функцией одной материальной точки с массой m, движущейся во внешнем поле U(r), симметричном относительно неподвижного начала координат.

Таким образом, задача о движении двух взаимодействующих материальных точек сводится решению задачи о движении одной точки в заданном внешнем поле U(r).

Выведем величины пороговых энергий для случая СЦМ и ЛСК систем координат.

СЦМ-система: В системе центра масс полный импульс равен нулю. В этом случае пороговая энергия, равная суммарной кинетической энергии во входном канале при условии, что в выходном канале частицы покоятся, может быть найдена из условия E^(вх)=E^(вых) или [T₁+T₂+(m₁+m₂)c²]=(m₃+m₄)c².

Отсюда

Е_пор=(T₁+T₂)=[(m₃+m₄)-(m₁+m₂)]c² или

Е_пор=Q, где Q-энергия реакции.

ЛСК-система: Из закона инвариантности квадрата четырёхвектора энергии-импульса

(Е²-р²с²=inv) и законов сохранения следует, что в пороге

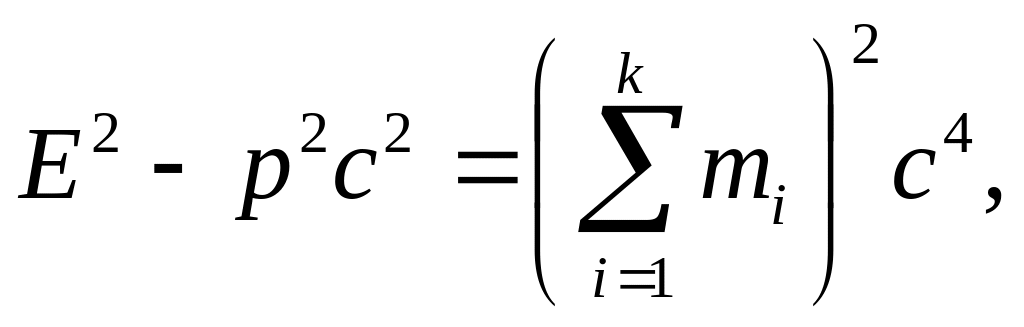так как в пороге в системе центра масс кинетическая энергия и полный импульс родившихся частиц равны нулю (здесь -сумма масс k-родившихся частиц). В ЛСК полная энергия будет , где m₁ и m₂ массы налетающей частицы и ядра мишени, соответственно. Для налетающей частицы

Отсюда 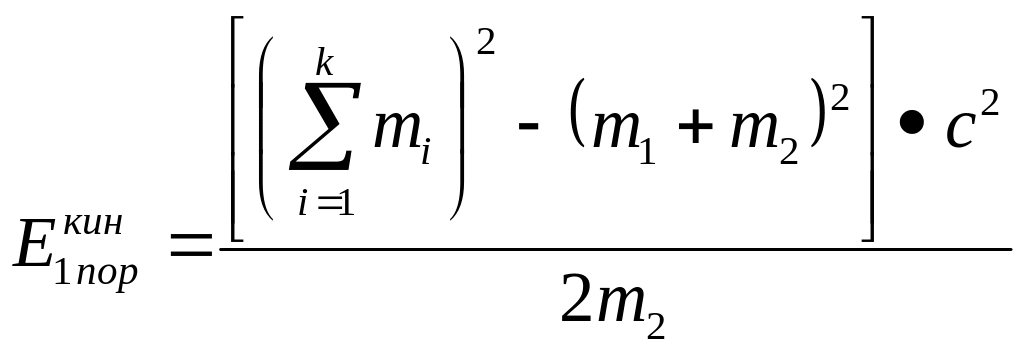. (8.3)

4. Механизмы ядерных реакций

   1. Составное ядро. Модель Бора.

Модель Бора основывается на предположении о протекании ядерной реакции в две стадии. На первой стадии реакции в результате слияния налетающей частицы ядра мишени образуется составное ядро С: a+А С b+B.

В компаунд-ядре С энергия возбуждения

делится среди А нуклонов, и этой остаточной энергии явно недостаточно, чтобы удалить нуклон из ядра. Лишь через t >> _nucl возможна концентрация достаточной энергии на одном из нуклонов, чтобы обеспечить его вылет из ядра. Таким образом, составное ядро «живёт» долго, так что «забывает» о способе своего образования. Поэтому сечение реакции через составное ядро можно записать в виде

_ab=_acW_b,

где _ac полное сечение реакции через составное ядро, а W_b –вероятность его распада по каналу b. Испускание нуклонов составным ядром напоминает испарение молекул из нагретой капли. В этом случае угловое распределение испущенных нейтронов в системе центра масс –изотропно.

Рассмотрим далее два предельных случая:

1) уровни составного ядра сильно перекрываются и образуют непрерывный спектр без особенностей;

2) уровни составного ядра принадлежат дискретному спектру и могут считаться изолированными.

Как в первом, так и втором случаях сечение образования составного ядра определяется следующими факторами:

• геометрический фактор, определяющий вероятность попадания частиц с орбитальным моментом l в область действия ядерных сил;

• коэффициент прилипания _l , характеризующего вероятность проникновения частицы с орбитальным моментом l в ядро и «захвата» его там.

Пусть имеется поток частиц (например, нейтронов) N частиц/см².

Частицы с орбитальным моментом l составляют долю потока , равную площади кольца со средним радиусом _l (см. рис. 8.2). Площадь этого кольца равна полуразности площадей кругов

в свою очередь .

.

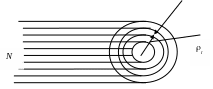
Рис. 8.2. Схематическое представление сечения рассеяния.

Для того, чтобы нейтрон попал в зону действия ядерных сил, очевидно, из всех возможных l надо брать лишь те, которые соответствуют предельному параметру, равного радиусу ядра ( .

Отсюда геометрическое сечение ₀ равно

Сечение ₀ определяет вероятность процесса, состоящего в том, что частица попадает в область действия ядерных сил. Для определения парциального (в зависимости от l) сечения образования составного ядра

надо найти коэффициент прилипания _l , значение которого определяется величиной центробежного барьера и вероятностью частицы остаться в нём. Влияние этих двух факторов определяет коэффициент пропускания потенциального барьера и в принципе может быть найден при квантовомеханическом расчёте.