6. Резонансная флюоресценция и эффект Мёссбауэра.

В 1904г. Рэлей предсказал, а Вуд экспериментально подтвердил существование резонансной флюоресценции, т.е. резонансного поглощения света. Следует отметить, что предсказание Рэлея было сделано на основе чисто классического (механического) описания резонансных явлений.

Затем были открытия Резерфорда, первая модель атома Бора, квантовомеханическое описание атома и соответственно осознание резонансной атомной флюоресценции как проявление свойств атомного объекта. Поэтому были все основания ожидать, что и для гамма-лучей, испускаемых или поглощаемых при переходах между энергетическими уровнями ядер, будет наблюдаться резонансная флюоресценция. Тем не менее, последняя либо не наблюдалась вовсе, либо наблюдалась в значительно ослабленном варианте. Чтобы понять этот парадокс следует сначала разобрать ситуацию с самим фактом проявления резонансной флюоресценции.

Ядро представляет собой связанную систему, которая может находиться в различных по энергии возбуждения состояниях. Последние, будучи стабильными относительно частичного распада, испытывают -распад или серию -распадов, приводящих в конечном счёте к основному состоянию.

Как известно из квантовой механики волновая функция состояния в зависимости от времени имеет вид:

. (5.39)

Если энергия Е данного состояния представляет собой величину действительную, то вероятность найти систему в данном состоянии не будет зависеть от времени, так как . Таким образом, в этом случае система оказывается стабильной. Чтобы экспоненциальный распад состояния (t) имел место, следует к энергии добавить малую мнимую часть:

(5.40)

где Е₀ и  действительные величины, а множитель ½ введён ради удобства. Принимая во внимание соотношение (5.40), для вероятности нахождения частицы в данном состоянии имеем

. (5.41)

С учётом соотношений (5.39) и (5.40) волновая функция распадающегося состояния имеет вид

. (5.42)

Таким образом, прибавление малой мнимой добавки к энергии позволяет описывать распад, протекающий по экспоненциальному закону. Чтобы выяснить имеет ли мнимая часть энергии физический смысл, заметим , что (t) в (5.42) является функцией времени. Спрашивается, какова вероятность, что испущенный квант имеет энергию Е. Для ответа на этот вопрос желательно иметь волновую функцию в виде функции энергии, а не времени. Перейти от (t) к (Е) можно с помощью преобразования Фурье. Рассмотрим функцию f(t). При общих предположениях её можно представить в виде интеграла

. (5.43)

Функция g() в этом интеграле играет ту же роль, что и коэффициенты разложения в обычном ряде Фурье. Обращение интеграла (5.43) имеет вид

. (5.44)

Возьмём в качестве f(t) функцию (t) в виде (5.42). Если распад начинается в момент t=0, то нижний предел интеграла можно положить равным нулю и функция g() примет вид

. (5.45)

Откуда

Функция g() пропорциональна амплитуде вероятности того, что частота  появляется в разложении Фурье для волновой функции (t). Поскольку Е= , плотность вероятности W(E) найти состояние с энергией Е пропорциональна величине :

. (5.46)

Условие .

Откуда W(E) окончательно принимает вид

. (5.47)

Таким образом, энергия распадающегося состояния не имеет точного значения. Малая мнимая добавка в формуле (5.39), введённая для описания распада состояния, приводит к уширению соответствующей линии спектра. Ширину линии , обусловленную распадом состояния, называют естественной шириной. Такая форма линии называется лоренцевской или брейт-вигнеровской.

Таким образом, можно подвести итог:

9. Всякий уровень характеризуется своей средней энергией Е₀;

10. Всякий уровень характеризуется естественной шириной ; Эта ширина связана со средней продолжительностью жизни  возбуждённого состояния соотношением неопределённости h/2=1.0510^-27эргсек.

11. Вероятность распада или, наоборот, резонансного возбуждения этого уровня квантом с энергией Е определяется дисперсионной формулой Брейта-Вигнера.

Соотношение (5.47) определяет также энергетическую зависимость сечения резонансного поглощения света (или -квантов) равного

W(E)= 4 g W(E),

где g –весовой фактор, равный отношению числа квантовых состояний возбуждённой системы к возможному числу квантовых состояний во входном канале

На практике форма  -линии оказывается несколько иной. Это происходит вследствие доплеровского уширения резонансной линии. Дело в том, что как излучающие, так и поглощающие атомы (или ядра) не покоятся, а находятся в тепловом движении. Частота кванта  относительно тел, движущихся с некоторой скоростью v под углом  к направлению движения квантов, испытывает доплеровский сдвиг

. Так как v_тепл<<c, то -₀==

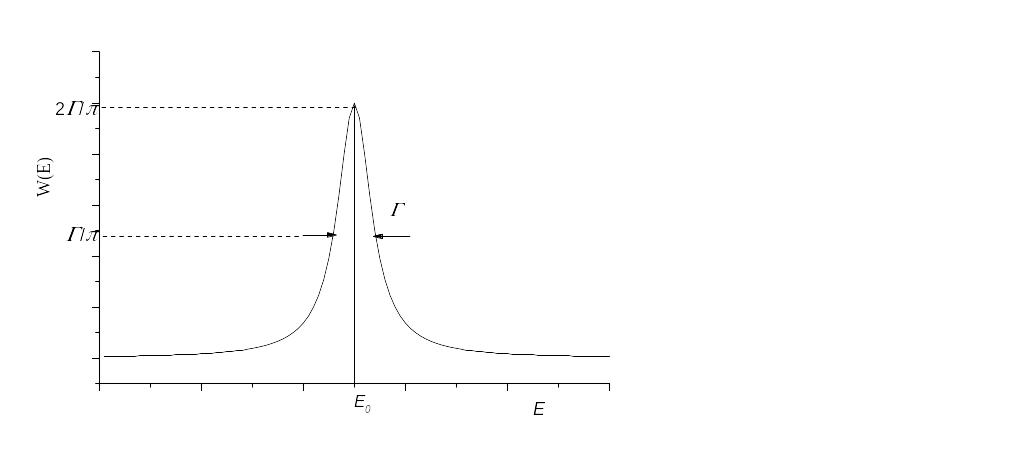
Рис. 5.7. Форма линии естественной ширины распадающегося состояния.

Пусть излучатель испускает строго монохроматические кванты с энергией Е₀. Тогда поглотитель, который движется навстречу воспринимает эту энергию как Е₀(1+ и наоборот. Таким образом, видно, что наша первоначально сколь угодно узкая линия превратится в полоску с шириной . Поскольку для теплового движения , то для D получаем . Таким образом, доплеровское уширение за счёт теплового движения не приводит к изменению полного интеграла по уширенному пику по сравнению с неуширенным, но резко снижает сечение поглощения в точке Е=Е₀=Е_рез.

Если бы дело обстояло только в доплеровском уширении за счёт теплового движения, то резонансное поглощение  -квантов было наблюдено гораздо раньше, чем его наблюдал Мёссбауэр. Достаточно было бы охладить излучатель и поглотитель. Есть ещё одно «но». В данном случае речь идёт о возникновении сдвига по энергии за счёт эффекта отдачи, о котором говорилось выше (5.38). В результате эффекта отдачи резонансные максимумы для излучателя и поглотителя оказываются удалёнными друг от друга на расстояние Е_отдачи (см. рис. 5.8), и, если Е_отдачи>>, то резонансная флюоресценция не может осуществиться.

В 1957г. немецкий физик Рудольф Мёссбауэр начал исследование резонансного поглощения гамма-квантов с энергией Е₀=129 кэВ, испускаемых возбуждёнными ядрами ¹⁹¹Ir, образующимися при -распаде материнского изотопа ¹⁹¹Os. При такой энергии гамма-квантов величина энергии отдачи R=0,046 эВ, и уже при комнатной температуре резонансные линии излучателя и поглотителя довольно сильно перекрываются. Желая ослабить роль такого перекрытия и измерить «фон» своей установки в отсутствии резонансного поглощения, Мёссбауэр поместил как излучатель, так и поглотитель в жидкий азот (Т88 К). При этом ожидалось, что пропускная способность поглотителя возрастёт. На самом деле всё произошло совсем наоборот.

Очень скоро Мёссбауэр понял смысл наблюдённого им парадокса, так как теория открытого эффекта была создана двадцатью годами ранее в работе Лэмба¹⁰, посвященной захвату нейтронов атомами, входящими в состав кристаллической решётки. Однако все эти двадцать лет учёные, работавшие с нейтронами и изучавшие их резонансное рассеяние (захват) и отлично знакомые с работой Лэмба, не догадывались о возможности непосредственного её приложения к резонансной флюоресценции. Те же, кто занимался резонансным рассеянием и поглощением -квантов, не использовали результатов, полученных в соседней области ядерной физики.

Поистине, узкий специалист подобен флюсу –полнота его одностороння!!

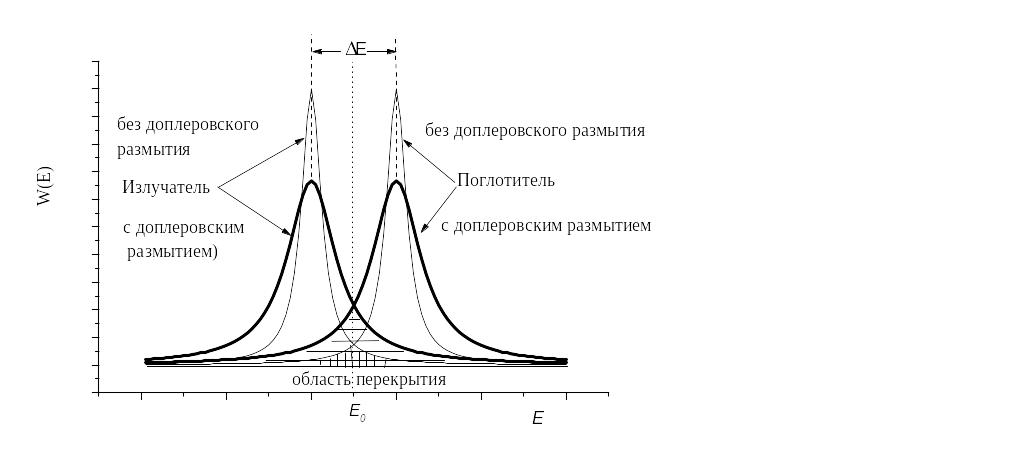
Рис. 5.8. Излучение и поглощение -квантов с учётом доплеровского уширения исходной линии и эффекта сдвига за счёт отдачи ядра.

В чём состоит причина усиления поглощения -квантов при понижении температуры в опыте Мёссбауэра¹¹. Она состоит в том, что, если атом -излучатель или –поглотитель входит в состав кристаллической решётки, то расчёт энергии отдачи для такого атома существенно не тот, что реализуется для свободных атомов. А именно, если энергии отдачи не достаточно для разрыва химических связей в решётке, то импульс отдачи становится достоянием всей решётки как целого, и в этом случае потеря энергии испущенным квантом будет в М_реш/М_изл раз меньше, чем в случае свободного атома. При этом в формулу для энергии отдачи входит не масса отдельного излучающего атома, а масса всей решётки, и тогда энергия отдачи становится ничтожно малой, так что отдача перестаёт препятствовать наблюдению резонансного рассеяния.(поглощения). Мало того, одновременно с исчезновением отдачи пропадает и доплеровское уширение -линии, так как допплеровское уширение, как и энергия отдачи определяются значениями масс излучателя и поглотителя. При этом доплеровская ширина оказывается много меньше естественной ширины.

В последующих простых и изящных экспериментах Мёссбауэр¹² окончательно подтвердил правильность объяснения наблюдённого им эффекта резонансной -флюоресценции без отдачи и в то же время дал основу экспериментальной методики всех последующих исследований этого явления.

Поскольку отношение естественной ширины резонанса к энергии ядерного перехода чрезвычайно мало (для ¹¹⁹Sn, например, Г/Е₀=10^-12), то достаточно ничтожных изменений энергии излучаемых  - квантов, чтобы существенно нарушить условия резонанса. Чтобы осуществить такие ничтожные изменения Мёссбауэр использовал эффект Доплера, но уже не при больших (до сотен метров в секунду) скоростях порядка c(R/E₀), использовавшихся для усиления резонансной флюоресценции в старых опытах, а при гораздо меньших скоростях –порядка c(Г/E₀). Принципиальная схема подобного эксперимента с использованием эффекта Доплера для варьирования энергии  -квантов представлена на рис. 5.9.

Детектор  - квантов регистрирует  -кванты, испускаемые источником и проходящие сквозь поглотитель, который может двигаться относительно источника с переменной скоростью v (+v- навстречу  -квантам и –v –по направлению их движения). Поскольку при движении поглотителя частота  и энергия E=h падающих на него  - квантов меняются вследствие эффекта Доплера: , то меняются и условия поглощения, коль скоро Е сравнимо с Г. В результате скорость счёта  -квантов оказывается зависящей от скорости движения поглотителя, как это схематически показано (для тонких источника и поглотителя) на рис. 5.9, и достигает минимального значения (максимум поглощения) при такой скорости движения, которая отвечает центру резонансной линии.

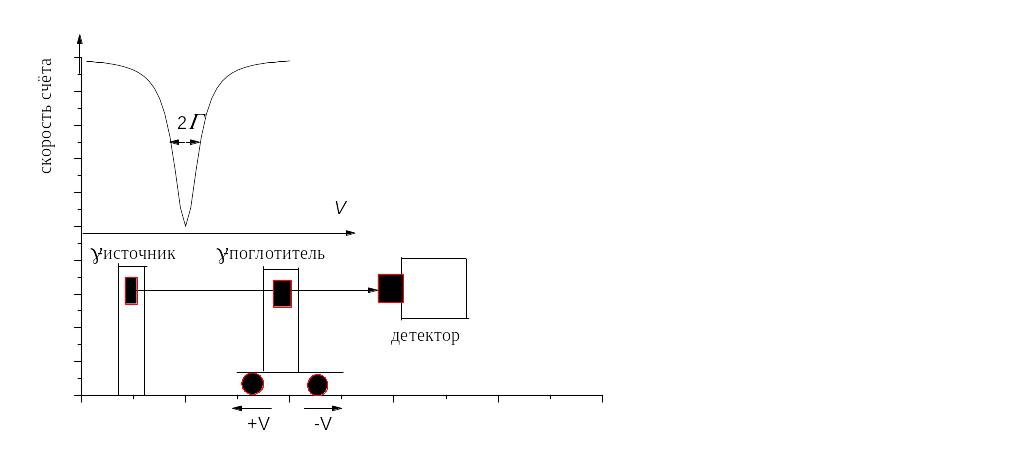
Рис. 5.9. Принципиальная схема по исследованию мёссбауэровского спектра поглощения в соответствующем эксперименте.

При полной идентичности излучателя и поглотителя центру резонансной линии соответствует v=0 (поглотитель покоится), в других случаях регистрируется смещение линии на величину . Под действием электрических и магнитных полей резонансная линия может расщепляться, и тогда в спектре поглощения наблюдается несколько резонансных минимумов.

Итак, эксперименты по наблюдению мёссбауэровских спектров сводятся к наблюдению зависимости поглощения (реже рассеяния) гамма-квантов в исследуемом образце от скорости движения этого образца относительно источника.

Лекция 6. Взаимодействие ионизирующего излучения с веществом

Для анализа результатов различных экспериментов, важно знать какие процессы происходят при взаимодействии частицы с веществом мишени. Регистрация частиц также происходит в результате их взаимодействия с веществом детектора.

Взаимодействие частиц с веществом зависит от их типа, заряда, массы и энергии. Заряженные частицы ионизируют атомы вещества, взаимодействуя с атомными электронами. Нейтроны и гамма-кванты, сталкиваясь с частицами в веществе, передают им свою энергию, вызывая ионизацию за счет вторичных заряженных частиц. В случае гамма-квантов основными процессами, приводящими к образованию заряженных частиц являются фотоэффект, эффект Комптона и рождение электрон-позитронных пар. Взаимодействие частиц зависит от таких характеристик вещества как плотность, атомный номер вещества, средний ионизационный потенциал вещества.

Каждое взаимодействие приводит к потере энергии частицей и изменению траектории её движения. В случае пучка заряженных частиц с кинетической энергией Е проходящих слой вещества их энергия уменьшается по мере прохождения вещества, разброс энергий увеличивается. Пучок расширяется за счет многократного рассеяния.

Между проходящей в среде частицей и частицами вещества (электронами, атомными ядрами) могут происходить различные реакции. Как правило их вероятность заметно меньше, чем вероятность ионизации. Однако реакции важны, в тех случаях, когда взаимодействующая с веществом частица является нейтральной. Например, нейтрино можно зарегистрировать по их взаимодействию с электронами вещества детектора или в результате их взаимодействия с нуклонами ядра. Нейтроны регистрируются по протонам отдачи или по ядерным реакциям, которые они вызывают.