1. Энергия связи ядра. Формула масс.

Один из наиболее поразительных фактов из экспериментальной ядерной физики заключается в том, что плотность массы в ядре приближенно постоянна для различных ядер: объем ядра пропорционален числу А нуклонов в нём. Подобный факт хорошо известен для обычных жидкостей, и, вероятно, поэтому одной из самых ранних моделей ядра, предложенной Бором² и фон Вейцзекером³, стала модель жидкой капли; в ней ядра рассматривались как практически несжимаемые капли жидкости чрезвычайно большой массовой плотности. Модель жидкой капли позволила понять характер зависимости энергии связи ядра от атомного номера, а также дала наглядную физическую картину процесса деления ядра. Энергия связи, как указывалось выше, можно представить формулой

W/c² = Zm_p + Nm_n - М(Z,N). (4.1)

На практике часто используют близкую к энергии связи величину, называемую дефектом массы, которая определяется как разность между энергией покоя атома M(Z,N) и произведением числа нуклонов A на u.

= M(Z,N)c² - Au (4.2)

Сравнивая (4.1) и (4.2), видим, что величины - и W по существу описывают одну и туже величину, хотя они и отличаются на некоторую очень малую энергию. Зависимость средней энергии связи в расчете на один нуклон (т.е. величина W/A) от числа нуклонов A показана на рис. 4.1. Эта кривая имеет ряд интересных особенностей.

1. Почти для всех стабильных ядер величина W/A лежит в коридоре 8-9 МэВ. Это постоянство является выражением эффекта насыщения ядерных сил. Это означает, что один нуклон притягивает лишь ограниченное число других частиц; остальные нуклоны либо вовсе не подвергаются его влиянию, либо отталкиваются им. Действительно, если бы каждый нуклон в ядре притягивался всеми другими нуклонами, то имелось бы А(А-1)/2 различных взаимодействующих пар. Естественно ожидать при этом, что энергия связи будет пропорциональной А(А-1)А², а диаметр ядра будет равен радиусу действия ядерных сил. Оба эти предсказания противоречат эксперименту при А>4; для большинства ядер объем и энергия связи пропорциональны массовому числу А.

Р ис. 4.1. Энергия связи в расчёте на один нуклон для разных ядер.

2. Величина W/A достигает максимума примерно для ядра железа (А60). При отходе от максимума она очень медленно спадает при больших А и быстрее при малых А. Такой характер поведения кривой позволяет легко понять основные способы получения ядерной энергии. Если ядро, например, с числом нуклонов А=240 разделится на два осколка с числами нуклонов А 120, то суммарная энергия связи обоих осколков будет больше, чем энергия связи исходного ядра, т.е. энергия будет освобождаться.

Такой процесс отвечает за получение энергии при реакции деления ядер. С другой стороны, если два легких ядра сольются вместе, то энергия связи слившегося ядра будет больше, чем сумма энергий двух исходных ядер, и энергия снова будет освобождаться. Это как раз та энергия, которая получается в реакции ядерного слияния.

Регулярность и постоянство кривой зависимости энергии связи W/A от числа нуклонов А наводят на мысль, что должна существовать простая формула для массы ядер. Первую такую полуэмпирическую формулу предложил Вейцзекер, который заметил, что постоянство средней энергии связи в расчет на один нуклон и постоянство плотности массы ядра непосредственно приводит к модели ядра в виде жидкой капли. Так как ядро содержит А нуклонов, объемный вклад Е_v в энергию связи ядра определяется формулой

Е_v=+А (4.3)

Нуклоны, располагающееся на поверхности ядра, имеют меньшее число связей с другими нуклонами, чем их внутренние партнеры, и поэтому для любого реального ядра конечных размеров нужно учитывать дополнительный поверхностный вклад Е_s в полную энергию, который пропорционален величине поверхности ядра и уменьшает полную энергию связи ядра:

Е_s=-A^2/3 (4.4)

Объемное и поверхностное слагаемые – это все, что можно извлечь из модели жидкой капли. Если учесть только эти два слагаемых в массовой формуле, то все изобарные ядра окажутся абсолютно устойчивыми независимо от значений N и Z. На практике это далеко не так. Для легких ядер устойчивыми являются изобарные ядра с равным числом протонов и нейтронов (N = Z); для тяжелых ядер устойчивыми изобарными ядрам будут ядра, для которых N > Z. Эту особенность диаграммы NZ (см. рис. 3.1) легко учесть, если включить в массовую формулу ещё два дополнительных слагаемых: симметрийную и кулоновскую энергии.

Слагаемое, отвечающее кулоновской энергии, возникает потому, что меж двумя протонами возникают электрические силы отталкивания. Эта кулоновская энергия стимулирует появление стабильных изобарных ядер с избытком нейтронов. Самую простую оценку величины кулоновской энергии можно получить, если сделать предположение, что заряд Ze однородно распределен по сфере радиусом R. Классическая энергия такого распределения равна . Тогда для ядра, имеющего форму шара с радиусом R=R₀A^1/3, согласно выше приведённой зависимости, кулоновская энергия будет равна

. (4.5)

Она тем меньше по абсолютной величине, чем меньше Z.

Экспериментальный факт, свидетельствующий о том, что стабильными являются не просто ядра с избытком нейтронов, а ядра, заключенные в узкой полосе на диаграмме NZ (см. рис. 3.1), можно объяснить, только добавляя в массовую формулу еще одно слагаемое - симметрийную энергию. Симметрийная энергия возникает по той причине, что вследствие принципа запрета Паули ядра, в которых нуклонов одного типа больше, чем другого, имеют намного меньшую энергию связи, чем ядра с одинаковым числом протонов и нейтронов.

(4.6)

Собирая вместе все перечисленные слагаемые для энергии связи ядра (N, Z), получаем следующую массовую формулу Вейцзекера для энергии связи:

W= (4.7)

Кроме перечисленных выше четырех членов (4.3-4.6) в формулу масс был впоследствии введен ещё один член , обусловленный спиновой зависимостью ядерных сил. Он возникает из-за того, что ядра, имеющие четное число нейтронов или протонов, обладают дополнительной энергией связи (эффект спаривания). По этому признаку все ядра разделяются на три группы:

• наиболее устойчивые четно-четные ядра (с четным N и четным Z, т.е. имеющие спаренные нейтроны и протоны);

• наименее устойчивые нечетно-нечетные ядра (с нечетным N и нечетным Z, т.е. имеющие по неспаренному нейтрону и протону);

• нечетные по А, т. е. четно-нечетные и нечетно-четные ( с четным N, нечетным Z и с нечетным N, четным Z).

(4.8)

В окончательном виде формула Вейцзекера выглядит как

, (4.9)

где =15,75 МэВ; =17,75 МэВ; =0,71 МэВ; =24,7 МэВ;

Помня, что масса ядра М(Z,N) = Zm_p + Nm_n - W/c² (см. (3.1)), формулу для массы ядра можно переписать в виде

М(Z,A)=Zm_p+(A-Z)m_n - . (4.10)

Найдем уравнение минимумов кривых, полученных пересечением массовой поверхности M(A,Z) плоскостями A=Z+N=const.

Выполним дифференцирование

Откуда для Z ядра, имеющего минимальную массу (максимальную энергию связи W) в изобарном семействе с массовым числом A,

(4.11)

Уравнение кривой, являющейся геометрическим местом точек минимальных значений масс в осях OZ, ON, OM, имеет вид

. (4.12)

Рассмотрим зависимость массы ядер изобар в зависимости от Z. Из уравнения (4.10) следует, что эта зависимость может быть представлена квадратичной параболой

(4.13)

где

.

Уравнение (4.13) для случая ядер с нечетным А характеризуют собой параболу с минимумом в точке Z=Z₀ (рис. 4.2).

В случае ядер с четным А возможны два случая: Z₀ приходится на четно-четное ядро и на нечетно-нечетное. В обоих случаях график M(Z,N) расщепляется на две эквидистантные параболы со смещением относительно друг друга 2, но в первом случае ядро с Z₀ находиться на нижней параболе (рис.4.3), и тогда в изобарном семействе имеется три стабильных ядра.

Во втором случае ядро (рис.4.4) с Z₀ находиться на верхней параболе, и тогда в изобарном семействе имеется два стабильных ядра с Z=Z₀-1 и Z=Z₀+1 или одно с Z=Z₀.

Из анализа формулы масс следует, что изобарное семейство с нечетным А имеет один ‑стабильный нуклид, все остальные члены семейства могут испытывать лишь один вид -распада: либо ^- -для Z<Z₀, либо ⁺-(включая и Е-захват) для Z>Z_0.

Изобарные семейства с четным А могут иметь три стабильных нуклида (Z четное) и два стабильных нуклида (Z нечетное),

Аналогичный анализ массовой поверхности может быть сделан для изотопных и изотонных семейств.

Таким образом, формула масс позволяет определить область стабильных относительно -распада ядер и предсказать вид -радиоактивности конкретного нуклида.

Рис. 4.2

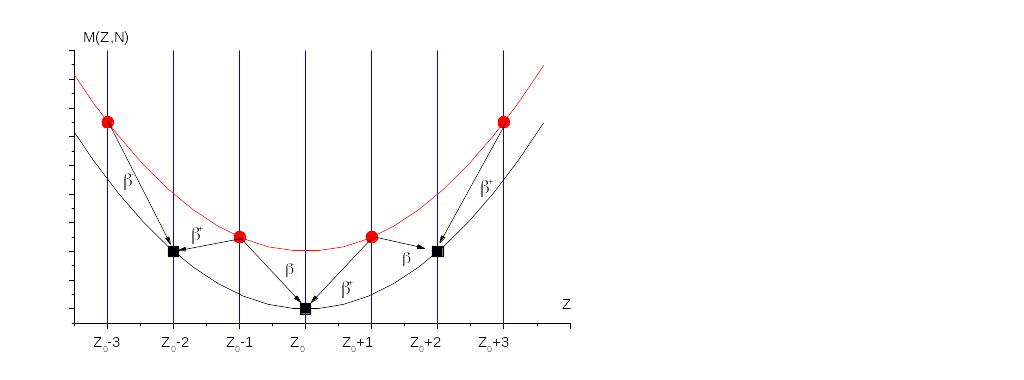Рис. 4.3

Рис. 4.4