5.3 Вычерчивание элементов зубчатого зацепления

Подсчитав все размеры элементов зацепления по вышепреведенным формулам, вычерчиваем зубчатое зацепление. Масштаб построения выбран таким образом, чтобы высота зуба на чертеже была не менее

50 мм  =0,26мм/мм

Строим касательную к основным окружностям, отрезок N1N2 касательной, заключенный между точками касания, является теоретической линией зацепления.

Отрезок аb теоретической линией зацепления, заключенный между точками пересечения ее с окружностями, выступов колес, называется активной частью линии зацепления. Зацепление зубьев начинается в точке а и заканчивается в точке b. При этом точка касания на профиле первого колеса (ведущего) перемещается от основания к вершине, на профиле второго колеса (ведомого) от вершины к основанию.

5.4 Построение активной части линии зацепления

Участки профилей зубьев, которые участвуют в зацеплении, называют рабочими. Для нахождения этих участков нужно на профиле зуба первого колеса найти точку, сопряженную с крайней точкой головки второго колеса, а на профиле зуба второго колеса – точку, сопряженную с крайней точкой головки первого колеса. Угол зацепления  (показан на чертеже)  =20

Коэффициент перекрытия по картине зацепления:

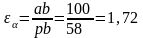
где 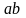- длинна активного участка линии зацепления;

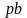- шаг основной окружности;

5.6 Расчёт планетарной передачи

Общее передаточное отношение привода:

Uобщ= nдв/n1,

где nдв – частота вращения электродвигателя,

n1 – частота вращения кривошипа.

Uобщ =1420/70=20,3

Так же из формулы

Uобщ = Uпл2Uab,

найдём Uпл, зная UАВ, найденного по формуле:

Ua,b=zb/za=25/14=1,79

где za, zb – числа зубьев колёс простой передачи

Uпл = Uобщ/UAB = 20,3/1,79=11,34

Так как планетарный редуктор имеет 2 одинаковые ступени, то передаточное отношение одной ступени:

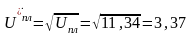
Uпл= U1,н(3)

где U1,H = 1- U(H)1,3.

U(H)1,3=U(H)1,2 · U(H)2,3 = - z3/z1

Uпл=1+z3/z1

Из условий соосности запишем U1,Н через числа зубьев, зная что

r3= r1+2·r2, а следовательно и z3= z1+2·z2 так как r=0,5·m·z.

Из этого следует что U1,Н=1+(z1+2·z2)/z1, то есть отсюда найдём

отношение: Z2/Z1=(3,37 – 2)/2=0,685

Получаем, что z1>z2. Для данной планетарной передачи я принимаю z2=22. Теперь расчитаем число зубьев второго колеса:

Z1=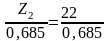 =32 тогда Z3=Z1+2Z2=32+44=76

Из условия соседства находим предельно допустимое число сателитов:

К≤180/arcsin(z2+2)/(z1+z2)= 180/arcsin(22+2)/(32+22)=6,5

Задаёмся числом сателлитов К= 6; и проверяем условие сборки

q=(z1+z2)/K=(22+32)/6=9

Так как число q = 9, то есть оно целое, значит расчёт провели верно и можно взять те числа зубьев которые мы принимали.

Определим радиусы делительных окружностей:

r1=mz1(z3,z2)/2

r1=332/2=48 мм

r2=322/2=33 мм

r3=376/2=114 мм

6. Проектирование кулачкового механизма

6.1 Задача проектирования кулачкового механизма

Довольно часто встречается задача синтеза кулачкового механизма. Она состоит в построении профиля кулачка по заданным законам движения кулачка и толкателя.