
- •«Механизмы вытяжного пресса»
- •1. Техническое задание
- •2. Структурный анализ рычажного механизма
- •2.1 Построение структурной схемы механизма
- •2.2 Структурная классификация механизма
- •3. Динамический анализ рычажного механизма по коэффициенту неравномерности движения
- •3.1 Построение планов положений механизма
- •3.2 Построение планов скоростей механизма
- •3.3 Расчет и построение графика приведенного момента сил полезного сопротивления
- •3.4 Построение графика работ сил полезного сопротивления и сил движущих
- •3.5 Построение графика приращения кинетической энергии
- •3.6 Расчет и построение графика приведенного момента инерции рычажного механизма
- •3.7 Построение диаграммы энергомасс (кривой Виттенбауэра)
- •3.8 Определение момента инерции маховика
- •4. Силовое исследование рычажного механизма
- •4.1 Задачи силового исследования
- •4.2 Построение плана механизма
- •4.3 Построение плана скоростей
- •4.3 Построение плана ускорений
- •4.4 Определение реакций в кинематических парах
- •5. Синтез эвольвентного зубчатого зацепления
- •5.1 Задачи синтеза зубчатого зацепления
- •5.2 Определение геометрических размеров зубчатого зацепления
- •5.3 Вычерчивание элементов зубчатого зацепления
- •5.4 Построение активной части линии зацепления
- •5.6 Расчёт планетарной передачи
- •6. Проектирование кулачкового механизма
- •6.1 Задача проектирования кулачкового механизма
- •6.2 Построение диаграмм движения толкателя
- •6.3 Определение минимального радиуса кулачка
- •6.4 Профилирование кулачка
4.4 Определение реакций в кинематических парах
Силовой расчет ведем по группам Асура, начиная с последней присоединенной группы 4-5. Трение в кинематических парах не учитывается.
Рассмотрим группу 4-5. Действие отброшенных связей заменим реакциями.
На звенья действуют:
- сила
полезного сопротивления
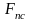 =32000
Н;
=32000
Н;
- сила
тяжести
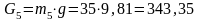 Н;
Н;
- главный вектор сил инерции
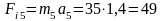 Н;
Н;
- главный момент сил инерции звена 4:
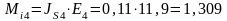 Н
м;
Н
м;
-
давление
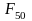 направляющих на ползун, давление
направляющих на ползун, давление
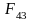 коромысла на шатун.
коромысла на шатун.
Условие равновесия группы 4-5:
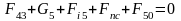
В этом уравнении 3 неизвестных, а именно: величина и направление и величина . Поэтому разложим на составляющие:
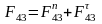 .
.
действующие
вдоль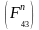 звена
звена
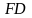 и перпендикулярно
и перпендикулярно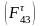 ему.
ему.
определим из
уравнения всех сил, действующих на шатун
FD относительно т.
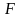
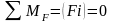
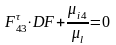
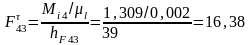 Н
Н
После этого уравнение примет вид:

По
этому уравнению строим план сил в
масштабе
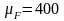 Н/мм.
Н/мм.
Масштабные длины сил:
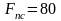 мм
мм
 мм
мм
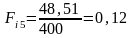 мм
мм
Все силы на плане откладываем в той последовательности, в которой они записаны. Точка пересечения линии действия и определит их величины.
Из плана сил имеем:
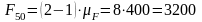 Н
Н
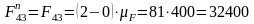 Н
Н
Рассмотрим равновесие группы 2-3
На звенья этой группы действуют:
- силы тяжести:
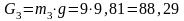 Н;
Н;
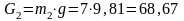 Н;
Н;
- силы инерции:
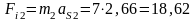 Н
Н
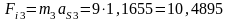 Н
Н
- моменты сил инерции:
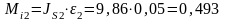 Н м
Н м
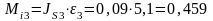 Н м
Н м
Реакции
опор:
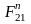 ,
,
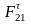 ,
,
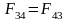
Рассмотрим равновесие группы 2-3 в целом:
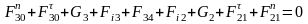
найдем из условия равновесия звена 2 относительно точки В:
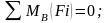
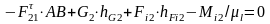
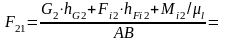
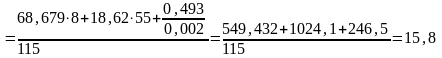 Н
Н
Рассмотрим равновесие звена 3 относительно т. В:
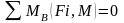
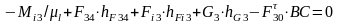
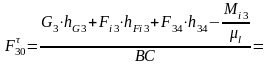 =
=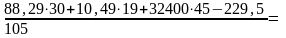
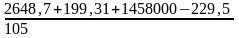 =13910,65Н
=13910,65Н
По
общему уравнению строим план сил в
масштабе
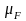 =400
Н/мм.
=400
Н/мм.
Масштабные длины сил:
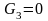 мм;
мм;
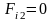 мм;
мм;
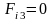 мм
мм
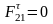 мм
мм
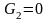 мм;
мм;
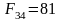 мм;
мм;
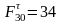 мм
мм
Ввиду
того, что силы
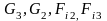 малы, план сил значительно упрощается.
малы, план сил значительно упрощается.
Из плана сил имеем:
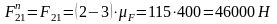
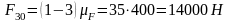
Рассмотрим
равновесие кривошипа и определим
уравновешивающий момент
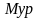 .
.
 ;
;
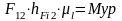
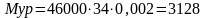 Н
Н
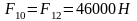
Проверяем результат методом рычага Жуковского.
В
качестве «рычага» выбираем план
скоростей, повернутый на 900, в одноименные
точки которого прикладываем все внешние
силы. Уравновешивающую силу
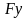 прикладываем в точке «а» плана скоростей
перпендикулярно ра.
прикладываем в точке «а» плана скоростей
перпендикулярно ра.
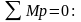
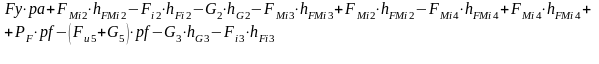
где
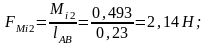
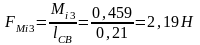
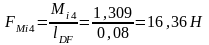
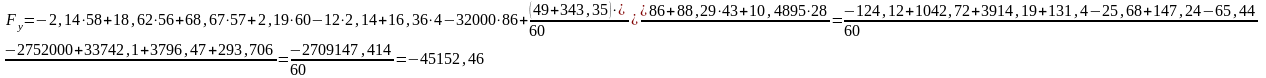
Знак минус показывает, что сила направлена по часовой стрелки.
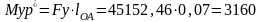 Н·м
Н·м
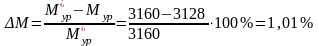
5. Синтез эвольвентного зубчатого зацепления
5.1 Задачи синтеза зубчатого зацепления
Зубчатая передача является одним из наиболее распространенных приводов, предназначенных для передачи вращения от одного вала к другому с заданным отношением угловых скоростей. Передача вращения сопровождается передачей крутящего момента, а следовательно, механической работы и мощности.
Зубчатые передачи в виде пары сцепляющихся колес могут воспроизводить лишь небольшие значения передаточных отношений.
5.2 Определение геометрических размеров зубчатого зацепления
Размеры колес, а также всего зубчатого зацепления зависят от чисел z1 и z2 зубьев колес, от модуля m зацепления, общего для обоих колес, а также от метода их обработки. Определяют размеры равно смещенного зубчатого зацепления при условии отсутствия подреза ножек зубьев. Все дальнейшие вычисления ведутся в мм:
Шаг зацепления по делительной окружности:
p = m
p =6·3,14=18,84 мм
Угловые шаги:
1= 2/zа=2·3,14/14=0,449
2=2/zв=2·3,14/25=0,251
2) Радиусы делительных окружностей:
r1 = mzа/2=6·14/2=42 мм
r2 = mzв/2=6·25/2=75 мм
Радиусы основных окружностей
rb1 = r1cos =42·cos200 = 39,47 мм
rb2 = r2cos= 75· cos200 =70,48 мм
где = 20 - угол профиля инструмента
Относительные смещения рейки (инструментальной) при нарезании колес:
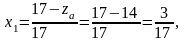
X1=3/17; X2=- X1 =-3/17
Толщины зубьев по делительной окружности:
S1 = m(/2 + 2x1tg),
S2 = m(/2 + 2x2tg),
S1 =6(1,57+23/17tg20)=10,188 мм
S2 = 6(1,57-23/17 tg20)=8,652 мм
Угол зацепления:
inv
= inv
+ 2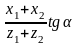
inv = inv=0,0149
Радиусы начальных окружностей:
r1 = r1=42 мм
r2 = r2 =75 мм
Межосевое расстояние:
a = rω1+rω2=42+75=117 мм
Радиусы окружностей впадин:
rf1 = 0,5m(z1 – 2,5 + 2x1);
rf2 = 0,5m(z2 – 2,5 + 2x2);
rf1 = 0,5 · 6(14 – 2,5 + 6/17)=35,6 мм
rf2 =0,5 · 6(25 –2,5 – 6/17)=66,4 мм
Радиусы окружностей вершин:
ra1 = a – rf2 – 0,25m;
ra2 = a – rf1 – 0,25m;
ra1 = 117– 66,4 –0,25 ·6=49,1 мм
ra2 =117 – 35,6 – 0,25 ·6=79,9
Радиальный зазор
C=c · m; c=0,25
C=0,256=1,5
