
- •«Механизмы вытяжного пресса»
- •1. Техническое задание
- •2. Структурный анализ рычажного механизма
- •2.1 Построение структурной схемы механизма
- •2.2 Структурная классификация механизма
- •3. Динамический анализ рычажного механизма по коэффициенту неравномерности движения
- •3.1 Построение планов положений механизма
- •3.2 Построение планов скоростей механизма
- •3.3 Расчет и построение графика приведенного момента сил полезного сопротивления
- •3.4 Построение графика работ сил полезного сопротивления и сил движущих
- •3.5 Построение графика приращения кинетической энергии
- •3.6 Расчет и построение графика приведенного момента инерции рычажного механизма
- •3.7 Построение диаграммы энергомасс (кривой Виттенбауэра)
- •3.8 Определение момента инерции маховика
- •4. Силовое исследование рычажного механизма
- •4.1 Задачи силового исследования
- •4.2 Построение плана механизма
- •4.3 Построение плана скоростей
- •4.3 Построение плана ускорений
- •4.4 Определение реакций в кинематических парах
- •5. Синтез эвольвентного зубчатого зацепления
- •5.1 Задачи синтеза зубчатого зацепления
- •5.2 Определение геометрических размеров зубчатого зацепления
- •5.3 Вычерчивание элементов зубчатого зацепления
- •5.4 Построение активной части линии зацепления
- •5.6 Расчёт планетарной передачи
- •6. Проектирование кулачкового механизма
- •6.1 Задача проектирования кулачкового механизма
- •6.2 Построение диаграмм движения толкателя
- •6.3 Определение минимального радиуса кулачка
- •6.4 Профилирование кулачка
3.7 Построение диаграммы энергомасс (кривой Виттенбауэра)
Построение
этой диаграммы выполняем путем исключения
параметра φ из диаграммы ∆Т(φ) и
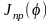 .
В результате этого получаем диаграмму
энергомасс.
.
В результате этого получаем диаграмму
энергомасс.
3.8 Определение момента инерции маховика
Обозначим постоянную составляющую приведенного момента инерции буквой I и найдем ее значение с учетом заданного коэффициента неравномерности движения.
Определим углы наклона касательных и кривой Виттенбауэра:
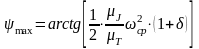 ;
;
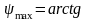 (0,5
0,08/106,127,332(1+1/6))=arctg0.0238=1,36
(0,5
0,08/106,127,332(1+1/6))=arctg0.0238=1,36
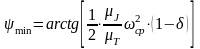 ;
;
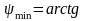 (0,5
0,08/106,127,332(1-1/6))=arctg0.017=0,97
(0,5
0,08/106,127,332(1-1/6))=arctg0.017=0,97
В этих
формулах
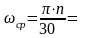 7,33
рад/с;
7,33
рад/с;
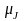 и
и
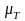 - масштабные коэффициенты диаграмм
энергомасс,
- масштабные коэффициенты диаграмм
энергомасс,
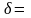 1/6
- взят из технического задания.
1/6
- взят из технического задания.
Под
углами
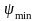 и
и
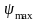 в крайних точках кривой Виттенбауэра
проводим две касательные с условием,
что они не будут пересекать эту кривую.
Касательные на оси ∆Т отсекут отрезок
ab, с помощью которого и находим потребную
постоянную составляющую приведенного
момента инерции рычажного механизма
(кг∙м2); обеспечивающую движение звена
приведения с заданным коэффициентом
неравномерности движения.
в крайних точках кривой Виттенбауэра
проводим две касательные с условием,
что они не будут пересекать эту кривую.
Касательные на оси ∆Т отсекут отрезок
ab, с помощью которого и находим потребную
постоянную составляющую приведенного
момента инерции рычажного механизма
(кг∙м2); обеспечивающую движение звена
приведения с заданным коэффициентом
неравномерности движения.
I=abT/2ср;
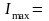 18106,12/(1/6)7,332=212,9кг·м2
18106,12/(1/6)7,332=212,9кг·м2
Диаметр маховика рассчитываем по формуле:
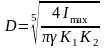
где К=b/D=0,05…0,15, принимаем К=0,1;
b-ширина маховика;
-плотность материала из которого изготовлен маховик, принимаем =7800 кг/м3=0,0078г/мм3
D=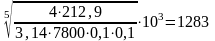 (мм)
(мм)
a=b=kd=0,11283=128,3 (мм)
4. Силовое исследование рычажного механизма
4.1 Задачи силового исследования
Задачами силового исследования являются определение реакций в кинематических парах и уравновешуещего момента на кривошипе от действия внешних сил и сил инерции.
Исследование проводим для положения механизма, когда сила вытяжки имеет максимальное значение.
4.2 Построение плана механизма
План механизма строим для своего положения при Fp=max в масштабе
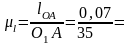 0,002
0,002 м/мм
м/мм
4.3 Построение плана скоростей
Для
исследуемого положения механизма строим
план скоростей в масштабе:
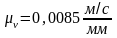
План скоростей строим повернутый на 900.
4.3 Построение плана ускорений
План ускорений строим на основании векторных уравнений для нахождения ускорений точек звена:
- ускорение точки А:
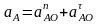
где
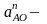 нормальная
составляющая ускорения т.А вокруг т.О1.
нормальная
составляющая ускорения т.А вокруг т.О1.
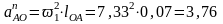 м/с2.
м/с2.
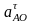 -
тангенциальная составляющая ускорения
т.А вокруг т.О1.
-
тангенциальная составляющая ускорения
т.А вокруг т.О1.
=0
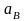 - ускорение точки
В:
- ускорение точки
В:

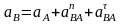
где
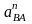 - нормальное ускорение т.В относительно
точки А
- нормальное ускорение т.В относительно
точки А
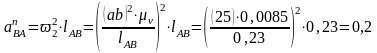 м/с2
м/с2
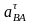 - тангенциальное
ускорение т.В относительно т.А.
- тангенциальное
ускорение т.В относительно т.А.
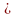 ВА
ВА
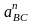 - нормальное
ускорение т.В относительно т.С
- нормальное
ускорение т.В относительно т.С
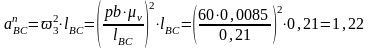 м/с2
м/с2
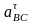 - тангенциальное
ускорение т. В относительно т. С
- тангенциальное
ускорение т. В относительно т. С
Ускорение точки D находим по теореме подобия:
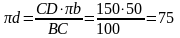 мм
мм
Ускорение точки F находим из векторных уравнений:
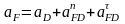 ;
;
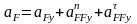 ;
;
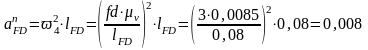 м/с2
м/с2
Из полюса откладываем вектор π нормального ускорения πа т.А, который направлен по кривошипу у центру О1.
πа=
120 мм;
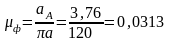
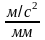
От т. а откладываем вектор нормального ускорения т.В относительно т. А, который направлен параллельно АВ.
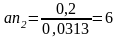 мм
мм
Через
конец вектора
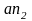 проводим линию перпендикулярно АВ. Из
полюса откладываем вектор
проводим линию перпендикулярно АВ. Из
полюса откладываем вектор
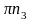 нормального ускорения т.В относительно
т.С;
нормального ускорения т.В относительно
т.С;
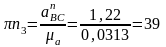 мм
мм
Через конец этого вектора проводим линию перпендикулярно ВС.
Пересечение 2-х линий, перпендикуляра к АВ и перпендикуляра к ВС, даст на плане ускорений т. b.
Вектор
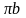 продолжаем и получаем вектор
продолжаем и получаем вектор
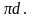
Далее
находим ускорение т. F, для этого к концу
вектора
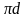 прибавляем
вектор
прибавляем
вектор
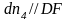
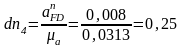 мм
мм
Через
конец этого вектора проводим линию
перпендикулярную DF до пересечения с
вертикалью, проведенной через полюс
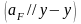 .
.
Из плана ускорений имеем:
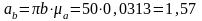 м/с2;
м/с2;
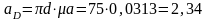 м/с2;
м/с2;
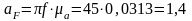 м/с2;
м/с2;
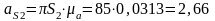 м/с2;
м/с2;
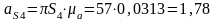 м/с2;
м/с2;
Угловые ускорения звеньев:
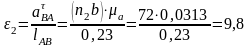 с-2;
с-2;
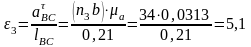 с-2;
с-2;
 с-2;
с-2;
