математический анализ. 3 семестр. Логинов А.С. 2005 г. loginov_1999@mail.ru

Глава 6. Интегралы, зависящие от параметра

§1. Собственные интегралы, зависящие от параметра

1. Непрерывность интеграла от параметра

Рассмотрим интеграл

F(y) =

для области вида

Где f определена в области D (замкнутая), x₁(y), x₂(y) непрерывные функции, определенные на [c,d].

Теорема. Если f непрерывна на D , x₁(y), x₂(y) непрерывны на [c,d], то F(y) непрерывна на [c,d].

Доказательство. |F(y+y) - F(y)| = =  ++ M|x₁|+(b - a) + M|x₂|.

Здесь используется ограниченность функции f и ее равномерная непрерывность.

Определение. Пусть функция f(x,y) определена на [a,b] для любого yY . Говорят, что f(x,y) равномерно сходится к g(x) на [a,b] при yy₀ если

 >0 >0x[a,b]yU_(y₀): |f(x,y) - g(x)|< .

Можно доказать, что если f(x,y) непрерывна и равномерно сходится к g(x) на [a,b] при yy₀ , то функция g(x) непрерывна на [a,b].

Теорема. Если f(x,y) непрерывна и равномерно сходится к g(x) на [a,b] при yy₀ , то

.

Доказательство. |b - a| .

2. Интегрирование интегралов зависящих от параметра

Предположим, что область является одновременно и областью типа А и В . Из формул выражения двойного интеграла через повторные следуют следующие формулы

F(y) =

3. Дифференцирование интегралов, зависящих от параметра

Теорема (Лейбниц). Если f и непрерывны в [a,b] [c,d] , то F(y) =

дифференцируема на [c,d] и .

Доказательство.

==, 0< <1. Тогда

.

Из этого неравенства и равномерной непрерывности функции следует требуемое утверждение.

Рассмотрим область типа В, указанную на рисунке и функцию f , определенную на прямоугольнике [a,b] [c,d], содержащем область D.

Теорема. Если f и ее производная непрерывны на [a,b] [c,d], x₁(y), x₂(y) имеют непрерывные на [c,d] производные, то F(y) = также имеет производную

+-.

Доказательство. Рассмотрим функцию Ф(y,u,v) = . Для нее существуют непрерывные частные производные (не очевидным является непрерывность функции ). Дифференцируя сложную функцию F(y) = = Ф(y, x₁(y), x₂(y)) получим требуемое равенство. Непрерывность функции = следует из равномерной непрерывности функции .

§2. Несобственные интегралы, зависящие от параметра

4. Равномерная сходимость несобственного интеграла от параметра

Рассмотрим интеграл

(1)

, yY.

Предположим, что при некоторых y интеграл (1) является несобственным. Так, если и при некотором y (1) имеет единственную особенность в b, то условием сходимости интеграла (1) будет существование конечного предела

.

Если при заданном y интеграл сходится, то для любого [a,b) интеграл (называемый остатком) будет существовать и условие сходимости можно записать в виде. В случае расходимости этого интеграла, естественно считать, что условие не выполнено. Таким образом, условие сходимости будет в дальнейшем записываться в виде

.

Определение. Сходящийся на Y интеграл называется равномерно сходящимся на Y, если

 >0 >0(b-,b)yY: (для интеграла 2-го рода)

 >0M(M,+)yY: (для интеграла 1-го рода)

Признак Вейерштрасса равномерной сходимости (для интеграла 2-го рода)

Если g(x) на [a,b), интегрируемая на любом [a, ), (b-,b) такая, что

1) |f(x,y)|  g(x), a  x < b, yY

2) сходится ,

то интеграл (1) сходится на Y.

Утверждение следует из неравенств .

Теорема. Пусть и f(x,y) определена и непрерывна на [a,b) на x для всех yY. Если для любых  функция f(x,y) равномерно сходится к g(x) на [a,b-] при yy₀ , интеграл равномерно сходится на Y, сходится. Тогда

.

Доказательство.

=.

можно сделать сколь угодно малым в силу равномерной сходимости функции f(x,y) к g(x). Интеграл можно сделать сколь угодно малым в силу равномерной сходимости интеграла . Интеграл можно сделать сколь угодно малым в силу сходимости интеграла .

Критерий Коши равномерной сходимости. Для равномерной сходимости интеграла необходимо и достаточно, чтобы

 >0>0 y  Y,(b-,b): .

Для доказательства можно рассмотреть функцию F()=. Сходимость интеграла при заданном y означает существование предела . Критерий Коши существования этого предела

5. Непрерывность интеграла от параметра

Теорема 2. Если f(x,y) определена и непрерывна на [a,b)[c,d] , интеграл (y) = сходится равномерно на [c,d] , то этот интеграл является непрерывной функцией.

Доказательство.

|(y+y) - (y)| =++.

Второй и третий интегралы могут быть сделаны меньше заданного  выбором  в силу равномерной сходимости интеграла . После выбора  первый интеграл может быть сделан меньше заданного  выбором достаточно мелкого разбиения в силу равномерной непрерывности функции.

6. Интегрирование интегралов зависящих от параметра

Теорема. Если функция f(x,y) определена и непрерывна на [a,b)[c,d], интеграл (y) = сходится равномерно на [c,d] , то

==.

Доказательство. Для любого  в разумных пределах

=. Отсюда следует требуемое утверждение, если учесть, что сходится равномерно на [c,d] к при b.

Эту теорему можно обобщить

Теорема. Если функция f(x,y) определена и непрерывна на [a,b)[c,d), интеграл сходится равномерно на  [c,] , интеграл сходится равномерно на  [a,] и существует один из повторных интегралов

,

, то существует и другой и выполняется равенство

=.

Без доказательства.

7. Дифференцирование интегралов, зависящих от параметра

Лемма. Если функция f(x,y) непрерывна на [a,b)[c,d] , то сходимость интеграла эквивалентна условию для любой последовательности _nb сходится ряд .

Аналогично для равномерной сходимости.

Теорема. Пусть функции f(x,y) и непрерывны на [a,b)[c,d] . Если сходится для всех y а сходится равномерно на [c,d] , то функция (y) = непрерывна дифференцируема на этом отрезке и

.

Доказательство. Пусть _nb . Согласно лемме

(y) = =, .

Далее применяется теорема о дифференцировании функционального ряда.

Пример. Гамма функция Эйлера Г(p) = , p > 0.

Непрерывность на (0, ).

Рассмотрим два интеграла , .

1)  , p[ , 1) . Признак Вейерштрасса.

- собственный для p[1 , ).

2)  , p[1 , A] . Признак Вейерштрасса.

 , p( 0 , 1] .

Докажем формулу

(1)

Для этого сделаем замену x  xy . (p) = ==.

2. Бета функция Эйлера В(p,q) = , p > 0 , q >0 .

Сделаем замену , dx = .

В(p,q) = =.

В(p,q) = (2)

3. Некоторые свойства функций Эйлера

Из формулы (1) следует, что

, . Интегрируя, получим . Откуда, используя (2)

Г В(p,q) = Г Г .

В(p,1-p) = Г Г ==.

Г(1) = 1, Г(p+1) = p Г(p).

Отметим, что из этой формулы следует, что Гамма функцию достаточно знать на интервале (0, 1/2).

Интеграл сходится равномерно на любом [ , A ], 0 <  < A. Поэтому интеграл можно дифференцировать по параметру. Рассмотрим интеграл .

В окрестности нуля |ln x|  для  > 0 существует C₁().

В окрестности бесконечности |ln x|  для  > 0 существует C₂().

Интеграл Г^(k)(p)= сходится равномерно на любом компакте. Это следует из оценок + , p[ , A]. Здесь для степеней логарифма справедливы оценки:

В окрестности нуля интеграл сходится при 0<<1, действительно т. к. x^-ln^kx = .

В окрестности бесконечности сходится, действительно

x^A-1|ln ^k x|  C x^A т. к. 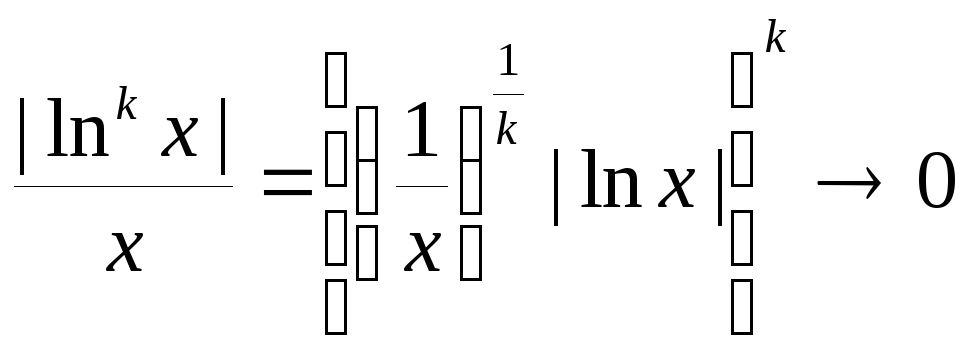и кроме того .

4. Примеры вычисления несобственных интегралов, зависящих от параметра

Формула Фруллани. Функция f(x) непрерывна и интеграл существует для любого A > 0.

=, ===== f(0).

= f(0).

Интегрированием по частям вычисляются интегралы

,   0, ,   0 .

Вычислить

.

, =+С.

==  С = 0.

Интеграл Пуассона

I = .

I ² = =====.

Интеграл I = .

Интегрирование по частям I = ==.

=I , , I = C , I(0) = ==, I = .

математический анализ. 3 семестр. Логинов А.С. 2005 г. loginov_1999@mail.ru 10