математический анализ. 3 семестр. Логинов А.С. 2005 г. loginov_1999@mail.ru

Глава 5. Преобразования базисов и координат, криволинейные координаты

§1. Преобразования базисов и координат

1. Взаимные, сопряженные базисы

В дальнейшем речь пойдет о базисах в трехмерном пространстве.

Определение. Базисы r_i , r^k называются взаимными или сопряженными, если выполнено условие (r_i , r^k) = .

Теорема. Для любого базиса r_i существует единственный взаимный базис.

Из условия r¹ r₂ , r¹ r₃ , поэтому этот вектор надо искать в виде c[r₂ , r₃], из условия (r₁ , r¹) = 1 находится множитель c. Таким образом,

r¹ = [r₂ , r₃]/( r₁ , r₂ , r₃ ), r² = [r₃ , r₁]/( r₁ , r₂ , r₃ ), r³ = [r₁ , r₂]/( r₁ , r₂ , r₃ ).

Любой вектор пространства можно разложить по базисам

x = x_k r^k = r_k x^k .

Координаты x_k называются ковариантными координатами, а x^k – контравариантными координатами.

Соглашение 1. В любом выражении состоящем из некоторого числа сомножителей наличие индекса у двух сомножителей на разных уровнях будет означать суммирование по этому индексу от 1 до 3.

Соглашение 2. Иногда, если не возникает путаницы, стрелка над вектором будет опускаться. Тоже самое касается жирности шрифта для обозначения вектора.

Например, формулы разложений по базисам будут выглядеть следующим образом

x = x_k r^k = r_k x^k .

Еще один пример: a_ic^j = a_ic^j .

Найдем выражение для ко и контравариантных координат

x = x_i rⁱ = r_i xⁱ 

x_i = (x, r_i ), xⁱ = (x, rⁱ) (1).

Подставляя выражения для координат в разложения вектора, получим формулы Гиббса

x = (x, r_i ) rⁱ = r_i (x, rⁱ) (2)

Подставим выражения x из формул Гиббса (2) в (1)

x_i = (x,r_j )(r^j,rⁱ) = x_j g^ji (3)

xⁱ = (r_j,r_i) (x,r^j ) = g_ji x^j (4)

Матрицы g^ji = (r^j,rⁱ), g_ji = (r_j,r_i) симметричны и называются метрическими тензорами. Беря в качестве x в формуле (2) вектора r_j , r^j получим формулы, связывающие векторы взаимных базисов с помощью метрических тензоров

r_j = g_ji rⁱ

r^j = r_i g^ji .

Подобные операции носят название операций поднимания и опускания индекса с помощью метрического тензора. Умножим первое равенство на r^k второе на r_k получим

= g_ji g^ik

= g_ik g^ji .

Эти равенства показывают, что матрицы метрических тензоров взаимно обратные.

2. Преобразование координат

Даны базисы e_i , r_i и eⁱ , rⁱ . Обозначим матрицы связывающие эти базисы ,,,.

r_i = e_j , e_i = r_j  = (5)

r^j = eⁱ , e^j = rⁱ  = (6)

Умножая первое равенство из (5) на e^k , а второе равенство из (6) на r_k получим выражения для матриц перехода между базисами

(r_i , e^k) = , (e^j , r_k ) =  (r_i , e^k ) = .

Таким образом, = . Аналогично показывается, что = . Равенства (5), (6) перепишутся в виде

r_i = e_j , e_i = r_j (7)

r^j = eⁱ , e^j = rⁱ (8)

Выпишем формулы преобразования координат при переходе к другому базису, например, для контравариантных координат.

x = r_i xⁱ , x = e_i yⁱ  (7) x = r_j yⁱ  x^j = yⁱ.

§2. Выражение операций теории поля в криволинейных координатах

1. Введение.

В дальнейшем будут использоваться следующие обозначения. С исходной декартовой системой координат xyz ( или x₁x₂x₃ ) связана криволинейная система координат x¹x²x³ отображением

или

Обозначим

r_i = .

2. Выражение градиента в криволинейных координатах

Для скалярного поля u градиент в декартовой системе координат равен

grad u = . По формуле дифференцирования сложной функции

=(grad u , r_i ) = u_i . По формулам Гиббса

grad u = (grad u , r_i ) rⁱ =u_i rⁱ .

Откуда

grad u = u_i rⁱ = u_i = u_i .

2. Выражение дивергенции в криволинейных координатах

Отметим, что для взаимно обратных отображений

и согласно правилам дифференцирования сложных функций справедливы соотношения или в матричном виде

= .

Таким образом, вектора являются сопряженными к

r_i = , т. е. r^j =, e_{i =} .

Обозначим V = Pi +Qj + Rk , V_i == , тогда

div V = =++=

= +

+ +

+ = (V₁,r¹)+(V₂,r²)+(V₃,r³) = (V_k,r^k) =

=.

В ряде случаев приходится рассматривать разложение исходного поля V по базису e_k : V = A^ke_k . В этом случае предварительно вычисляют производные V_k и полученные выражения подставляют в формулу для данной операции, например, в формулу div V =. Можно показать, что div V = .

4. Выражение ротора в криволинейных координатах

V = Pi +Qj + Rk , V_i == ,

rot V = ==

=

= =[r^k , V_k]= [r_k , V_k]= [e_k , V_k].

2. Выражение оператора Лапласа в криволинейных координатах

grad u = , , A^k = , div grad u = (r^k , V_k). Тогда из формулы div V = получим u = div grad u = .

§3. Выражение операций теории поля в цилиндрических координатах

1. Цилиндрические координаты (r, , h) = (x¹,x²,x³).

x = r cos 

y = r sin 

z = h

r1 = (cos  , sin  , 0), H1 = |r1| = 1, r2 = (-r sin  ,r cos  , 0), H2 = |r2| = r, r3 = ( 0 , 0 , 1), H3 = 1.

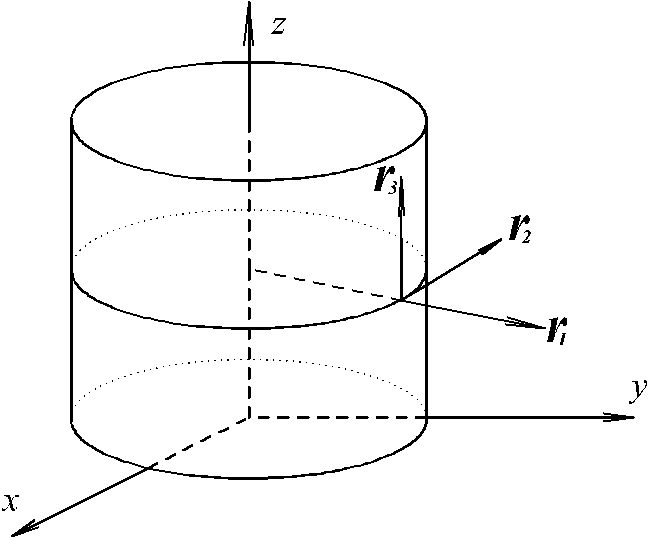
e₁ = e_r = (cos  , sin  , 0) ,

e₂ = e_ = (-sin  ,cos  , 0) ,

e₃ = e_h = ( 0 , 0 , 1) .

Базис e_r , e_ , e_z – ортонормированный.

,

, , ,

.

2. Выражение градиента в цилиндрических координатах

grad u = u_i rⁱ = u_i = u_i .

grad u = r₁ + r₂ + r₃ = e_r + e_ + e_z .

2. Выражение дивергенции в цилиндрических координатах

V = Pi +Qj + Rk , V_i == , V₁ = , V₂ = , V₃ = ,тогда

V = A^ke_k ,

V₁ = V_r = ( A^ke_k) = e_k A^k + A^ke_k = e_k A^k .

V₂ = V_ = ( A^ke_k) = e_k A^k + A^ke_k = e_k A^k + A¹e₂ - A²e₁ .

V₃ = V_h = ( A^ke_k) = e_k A^k + A^ke_k = e_k A^k .

Отсюда следует

div V = (V_k,r^k) = = =_.

4. Выражение ротора в цилиндрических координатах

[e₁, e₂]=e₃ , [e₃, e₁]=e₂ , [e₂, e₃]=e₁ ,

[e₁, V₁] = [e₁, e₂] + [e₁, e₃] = e₃ - e₂,

[e₂, V₂] = = ,

[e₃, V₃] = [e₃, e₁] + [e₃, e₂] = e₂ - e₁ ,

rot V =++.

5. Выражение оператора Лапласа в цилиндрических координатах

H = H₁ H₂ H₃ = r,

u = div grad u = = =.

§4. Выражение операций теории поля в сферических координатах

1. Сферические координаты (, , ) = (x¹,x²,x³).

x =  cos  cos 

y =  cos  sin 

z =  sin 

r1 = (cos  cos  , cos  sin  , sin ), H1 = |r1| = 1, r2 = (- cos  sin  ,  cos  cos  , 0), H2 = |r2| =  cos , r3 = (- sin  cos  , - sin  sin  ,  cos ), H3 = .

e₁ = e_ = (cos  cos  , cos  sin  , sin ),

e₂ = e_ = (- sin  , cos  , 0),

e₃ = e_ = (- sin  cos  , - sin  sin  , cos ).

Базис e_ , e_ , e_ – ортонормированный.

,

= cos  e₂ , = - cos  e₁ + sin  e₃ , = - sin  e₂ ,

= e₃ , = 0 , = - e₁ .

2. Выражение градиента в сферических координатах

grad u = ui ri = ui = ui .

grad u = r₁ + r₂ + r₃ = e_ + e_ + e_

2. Выражение дивергенции в сферических координатах

Пусть V = A^ke_k ,

V₁ = V_ = ( A^ke_k) = e_k + A^k = e_k .

V₂ = V_ = ( A^ke_k) = e_k + A^k =

= e_k – A² cos  e₁ - A³sin  e₂ + A² sin  e₃ .

V₃ = V_h = ( A^ke_k) = e_k + A^k = e_k + A¹e₃ – A³e₁ .

Отсюда следует

div V = (V_k,r^k) = = (V₁,e₁) (V₂,e₂) + (V₃,e₃) = + +.

4. Выражение ротора в сферических координатах

[e₁, e₂]=e₃ , [e₃, e₁]=e₂ , [e₂, e₃]=e₁ ,

[e₁, V₁] = [e₁, e₂] + [e₁, e₃] = e₃ - e₂,

[e₂, V₂] = = = =

,

[e₃, V₃] = [e₃, e₁] + [e₃, e₂] [e₃, e₁] =

= e₂ e₁ ,