Билет№2 Операции над множествами. Их свойства. Иллюстрация свойств операций над множествами на диаграммах Венна. Операции над множествами рассматриваются для получения новых множеств из уже существующих. перации над множествами рассматриваются для получения новых множеств из уже существующих.

О пределение. Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В .

 

Определение. Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В . Определение. Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В.

 

О пределение. Симметрической разностью множеств А и В называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В.

 

О пределение. Абсолютным дополнением множества А называется множество всех тех элементов, которые не принадлежат множеству А .

  Свойства операций над множествами

Билет№3

Понятие числовой функции в общем случае, пример. Понятие функции одной переменной, ее области определения. Примеры. Общее понятие функции: Пусть даны два множества А и В, функцией из множества А в множестве В называется всякое соответствие, при котором каждому элементу из А сопоставляется один, однозначно определенный, элемент из В. f: А→В, где А-обл. определения, В – обл. «прибытия» хͼ А y= f(x) ͼ B

Понятие числовой функции: Если область «прибытия» является числовым множеством, то функция называется числовой.

Пример: (те же примеры что и при функции одной переменной) Понятие функции одной переменной,ее области определения Если область «прибытия» и область определения функции являются числовыми множествами, то эта числовая функция является функцией одной переменной. Множество  называют областью определения функции   . Говорят также, что задана независимая переменная , которая может принимать частные значения  из множества , и каждому  в силу упомянутого закона приведено в соответствие определенное значение другой переменной   , называемой функцией или зависимой переменной.

Пример областями определения приведенных функций являются соответственно:

1) отрезок ; 2) множество ; 3) вся действительная ось; 4) вся действительная ось, из которой исключена точка   ; 5) отрезок . Билет №4

График функции одной переменной : Пусть   - множество чисел и пусть каждому числу   из   приведено в соответствие  одно число  , тогда говорят, что на    задана функция, которую записывают так:

Свойство: Функцией из множества А в множество В называется всякое соответствие, при котором каждому элементу из А сопоставляется один, однозначно определенный элемент из В.

Пример: f(x) = отец x – однозначно =>  это функция

F(n) = наибольший натуральный делитель n – однозначно => функция

Нормальные примеры: y=kx+b ; y=x^2n ; y= sin x, y=a^x

                     

Билет№5

Свойство ограниченности f-ции одн.переменной:

Число A ϵ R называется пределом функции f(x) в точке a или при x ->a и это обозначается следующим образом limx-> af(x) = A, если Для любого ε > 0 существует δ (ε) > 0: для любого x: 0 < |x-a| < δ, =>|f(x)-a| < ε

Cвойство ограниченности графически означает, что если функция ограничена снизу, то ее график целиком расположен выше некоторой горизонтальной прямой у = т ; если функция ограничена сверху, то ее график целиком расположен ниже некоторой горизонтальной прямой у = М .

Примером функции, определенной и возрастающей на всей числовой прямой, являющейся при этом ограниченной можно считать функцию y= arctgx.

Монотонная функция:

Возрастающие и убывающие функции объединяют общим понятием: монотонные функции.

Монотонная функция – это функция, меняющаяся в одном и том же направлении.

Функция возрастает, если большему значению аргумента соответствует большее значение функции. Говоря иначе, если при возрастании значения x значение y тоже возрастает, то это возрастающая функция.

Функция убывает, если большему значению аргумента соответствует меньшее значение функции. Говоря иначе, если при возрастании значения x значение y убывает, то это убывающая функция.

Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.

Функция постоянна (немонотонна), если она не убывает и не возрастает.

Ее св-ва:

 1) Сумма нескольких возрастающих функций является возрастающей функцией.

2) Произведение неотрицательных возрастающих функций есть возрастающая функция.

3) Если функция f возрастает и сохраняет знак, то функция 1/f убывает.

4) Если функция f возрастает и неотрицательна, то fn тоже возрастает (n ∈ N).

5) Композиция g (f (x)) возрастающих функций f и g также возрастает.

6) Если функция f возрастает, то функции cf (c > 0) и f + c также возрастают, а функция cf (c < 0) убывает (c – некоторая константа).

Билет №6. Линейная функция и Степенная функция. Их графики

Линейная функция — функция вида

 (для функций одной переменной).

Основное свойство линейных функций: приращение функции пропорционально приращению аргумента.

 является тангенсом угла, который образует прямая с положительным направлением оси абсцисс.

• При  , прямая образует острый угол с осью абсцисс.

• При  , прямая образует тупой угол с осью абсцисс.

• При  , прямая параллельна оси абсцисс.

b является показателем ординаты точки пересечения прямой с осью ординат. При  , прямая проходит через начало координат.

Y=kx+b, k<0

Y=kx+b, k>0

Степенна́я фу́нкция — функция  , где   (показатель степени) — некоторое вещественное число. К степенным часто относят и функцию вида  , гдеk — некоторый масштабный множитель.

Область определения

Если показатель степени — целое число, то можно рассматривать степенную функцию на всей числовой прямой (кроме, возможно, нуля). В общем случае степенная функция определена при  . Если  , то функция определена также и при  , иначе нуль является её особой точкой.

Рациональный показатель степени

Графики степенной функции при натуральном показателе n называются параболами порядка n. При   получается функция  , называемая прямой пропорциональной зависимостью.

Графики функций вида  , где n — натуральное число, называются гиперболами порядка n. При   получается функция  , называемая обратной пропорциональной зависимостью.

Графики степенных функций:

1)y=x²ⁿ

2)y=x²ⁿ⁺¹

3)y=x^-n

Билет№7. Градиент функции двух переменных и его свойства.

Градиент функции – это вектор, координаты которого являются частными производными этой функции.

Z=f(x;y) градиент Z={z’x;z’y}

U=f(x1; x2…; xn) gradU=(u’ x1 ; u’ x2…;u’ xn)

Свойства градиента:

1. Градиент показывает направление максимального возрастания функции.

2. В каждой точке области определения градиент перпендикулярен линии уровня, проходящей через эту точку(то есть касательной к линии уровня)

3. Производная по направлению вектора, перпендикулярного к вектору gradu, равна нулю.

Пример: Z= √x^2 +y^2

Z’x = x/ √ x^2 +y^2 Z’y = y/ √x^2 +y^2 gradZ={ x/ √ x^2 +y^2 ; y/ √x^2 +y^2}

C= √x^2 +y^2

Билет №8.

Показательная ф-ция – одна из основных элементарных ф-ций, имеет вид y=a^x , а>0, а(не)=0. Свойства: 1) а⁰ =1; 2)a^x+y =a^xa^y ; 3)(ax)y=axy; 4)(ab)^x=a^xb^x Используя функцию натурального логарифма lnx, можно выразить показательную функцию с произвольным положительным основанием через экспоненту: a^x=e^x*lna

Для а>1: для 0<a<1:

Билет №9.

Логарифмическая ф-ция - одна из основных элементарных ф-ций, имеет вид y=log_ax, a>0, a(не)=1.Св-ва: 1)основное логарифм.тождество: ; 2) Логарифмы единицы и числа, равного основанию: log_a1=0; log_aa=1; 3) Логарифм произведения, частного от деления, степени и корня: log_a(xy)=log_ax+log_ay; ; ; 4) Замена основания логарифма: ; .

Билет №10. Числовые последовательности и способы их задания. Примеры.

Последовательностью называется числовая функция f_n, заданная на множестве натуральных чисел N.

Обозначается через a_n, (a_n), {a_n}. Если n  - натуральное число, а a_n - значение последовательности в тоске n, то n  - номер числа a,  а само число a_n - общий или n-ый член последовательности.

График - изолированное множество точек плоскости.

Способы задания числовых последовательностей:

1) формулой n-го члена.  1, 4, 9, 16, 25, 36, ... … 2) описания членов 2, 4, 6, 8, 10, ... ... 1, 3, 5, 7, 9, ... ... 3) рекуррентным 1, 1, 2, 3, 5, 8, 13, 21, ...  a_n = a_n-1 + a_n-2 , …

Пример.

Последовательность Фибоначчи.

Проблема с кроликами: человек пару кроликов в загон, окруженный со всех сторон стеной. Сколько пар кроликов за год может произвести на свет эта пара, если известно, что каждый месяц, начиная со второго,  каждая пара кроликов производит на свет одну пару?

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

Ряд,  каждый член в котором - сумма двух предыдущих.

Билет №11. Определение предела числовой последовательности. Пример.

Число a называется пределом числовой последовательности {a_n}, если для любого, сколь угодно малого положительного числа ԑ>0, найдется такое число N (зависящее от ԑ, N=N_ԑ), что для всех членов последовательности с номерами n>N верно неравенство  .

Если это выполняется, то пишут или при n ∞

Последовательность может быть сходящаяся/расходящаяся.

Используя логические символы определение

Смысл определения: для достаточно больших n члены последовательности {a_n} как угодно мало отличаются от числа a  (по абсолютной величине меньше, чем на число ԑ, каким бы малым оно ни было).

Пример.

С ростом номера n число a_n становится все ближе к 1. 

Билет №12. Отрицание определения предела последовательности. Пример последовательности не имеющей предела.

Построение отрицаний

Х,У- люди

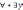х любит у

Отрицает х у х не любит у

Предела lim sin x не существует



Хотелось бы, чтобы вы почувствовали, что это так. Чтобы предел существовал, надо, чтобы при стремлении х → +

значения sin x приближались к какому-то конечному значению, либо стремились бы к бесконечности. А тут значения sin x колеблются между –1 и +1, не имея тенденции приближаться к какому-нибудь числу.

Билет №13. Бесконечно малые и бесконечно большие последовательности и их свойства.

Свойства бесконечно малых и бесконечно больших последовательностей

• Сумма двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.

• Разность двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.

• Алгебраическая сумма любого конечного числа бесконечно малых последовательностей сама также является бесконечно малой последовательностью.

• Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.

• Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

• Любая бесконечно малая последовательность ограничена.

• Если стационарная последовательность является бесконечно малой, то все её элементы, начиная с некоторого, равны нулю.

• Если вся бесконечно малая последовательность состоит из одинаковых элементов, то эти элементы — нули.

• Если — бесконечно большая последовательность, не содержащая нулевых членов, то существует последовательность , которая является бесконечно малой. Если же всё же содержит нулевые элементы, то последовательность всё равно может быть определена, начиная с некоторого номера , и всё равно будет бесконечно малой.

• Если — бесконечно малая последовательность, не содержащая нулевых членов, то существует последовательность , которая является бесконечно большой. Если же всё же содержит нулевые элементы, то последовательность всё равно может быть определена, начиная с некоторого номера , и всё равно будет бесконечно большой.

Билет №14.

Теорема о переходе к пределу в неравенства: Если   или    на   и существуют    и  , то  .

Теорема о 2х полицейских: Т: Пусть даны три последовательности: {Xn}, {Yn}, {Zn}. Причем Xn<=Yn<=Zn. При этом существует limXn=a=limZn (при n→∞), тогда limYn=a (при n→∞)

Доказательство:

1) Докажем, что Zn-Xn – бесконечно малая последовательность (бм)

Zn-Xn=Zn - a +a - Xn (Zn – a есть бм, + a – Xn – есть бм) => б.малая!

2) Докажем: Yn – Xn – бесконечно малая

0≤ Yn - Xn≤ Zn – Xn (а это бесконечно малая посл.) для любого E>0 существует N для каждого из которых n>N

|Zn – Xn| < E => |Yn – Xn| < E

Zn – Xn<E => Yn – Xn<E

3) Докажем: Yn – a – б.мал.

Yn - a = (Yn – Xn /есть б.мал.) + (Xn – a/ есть б.мал) – сумма б.малых есть б.малая.

Доказать: lim(2^n/n!)=0 при n→∞ 2^n/n!=2/1*2/3*2/4*…*2/n<< 2*1*(2/3)^(n-2) 0<2^n/n!< 2*(2/3)^(n-2). И придел от нуля, и придел от 2*(2/3)^(n-2) при n→∞ =0, то и lim(2^n/n!)=0.

Билет№15. Ограниченные последовательности. Теорема о существовании предела ограниченной последовательности. Число е.

Ограниченные последовательности:

Последовательность Yn называется ограниченной сверху, если существует такое число U, что Yn<или =U для любых номеров n. При этом число U называется верхней границей последовательности.

Последовательность Yn называется ограниченной снизу, если существует такое число L, что Yn>или=L для любых номеров n. Число L называется нижней границей последовательности.

Последовательность Yn называется ограниченной, если существуют такие числа L и U, что L<или=Yn< или=U для всех n = 1,2,3,…

Т1. Любая ограниченная сверху последовательность имеет наименьшую верхнюю границу.

Т2. Любая ограниченная снизу последовательность имеет наибольшую нижнюю границу.

Теорема о существовании предела ограниченной последовательности (теорема Вейерштрасса)

Если последовательность ограничена сверху и монотонно возрастает, то она обязана иметь предел. Аналогичное утверждение существует для убывающей последовательности.

X1 X2 Xn Х(n+1) а М

Определение: Последовательность Xn не убывает(не возрастает),если для

Определение: Последовательность Xn возрастает(убывает), если для

Определение: Строго возрастающая или строго убывающая последовательность называется монотонной последовательностью.

Теорема. Если Xn не убывает и ограничена сверху, то она сходится. Если Xn не возрастает и ограничена снизу, то она сходится.

Доказательство. При выполнении условия теоремы последовательность Xn ограниченна.

В силу ограниченности ,

• Если последовательность не убывает, то

• Если последовательность не возрастает, то

Рассмотрим первый случай.

По определению:

Т.к. Xn не убывает, то при

Второй случай рассматривается аналогично.

Число е.

e — математическая константа, основание натурального логарифма, трансцендентное число. Иногда число e называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e».Число e играет важную роль в дифференциальном и интегральном исчислении, а также во многих других разделах математики.

Способы определения:

1)Через предел(второй замечательный предел)

2)как сумма ряда

или

3)через определенный интеграл

4)как единственное число a, для которого выполняется:

5) Как единственное положительное число a, для которого верно:

Свойства:

Данное свойство играет важную роль в решении дифференциальных уравнений. Так, например, единственным решением дифференциального уравнения

является функция , где где c — произвольная константа.

Число e иррационально и даже трансцендентно. Его трансцендентность была доказана только в 1873 году Шарлем Эрмитом. Предполагается, что e — нормальное число, то есть вероятность появления разных цифр в его записи одинакова.

Доказательства иррациональности:

• Число e является вычислимым (а значит, и арифметическим) числом.

• (формула Эйлера)

• Ещё формулы, связывающие числа е и π

• «интеграл Пуассона» или «интеграл Гаусса»

5)предел

• Для любого комплексного числа z верны следующие равенства:

• Число e разлагается в бесконечную цепную дробь следующим образом:

Билет№ 16.

Предел функции. Определение через окрестность. Графическая иллюстрация.

=a

Значение a называется пределом функции f(x) в точке , если для любого 0

выполняется неравенство .

Билет№ 17. Предел функции. Определение через пределы последовательности. Доказать, что функция Дирихле ни в одной точке не имеет предела.

З начение a называется пределом функции    в точке  , если для любой последовательности точек , стремящейся к  , но не содержащей   в качестве одного из своих элементов (то есть в проколотой окрестности   ), последовательность значений функции   стремится к а.

Функция Дирихле́ — функция, принимающая значение 1, если аргумент есть рациональное число, и значение 0, если аргумент есть иррациональное число.

Функция Дирихле́ является всюду разрывной функцией: во всякой окрестности каждой точки вещественной прямой содержатся как рациональные, так и иррациональные числа, и, следовательно, данная функция не будет иметь предела ни в одной точке области определения.

Действительно, если выбрать последовательность рациональных чисел, стремящихся к a, то соответствующая последовательность значений функции стремится к единице. Если выбрать последовательность иррациональных значений, то значения функции стремится к нулю. Следовательно, на основании определения через пределы последовательностей данная функция не имеет предела.