Надежность систем, работающих до первого отказа (показатели, методы расчета)
Под элементом, работающим до первого отказа, понимается невосстанавливаемый элемент, которой после выхода из строя не может быть отремонтирован.
Для невосстанавливаемых систем, чаще всего, используются четыре показателя надежности: вероятность безотказной работы P(t), плотность вероятности отказов (частота отказов) f(t), интенсивность отказов λ(t), среднее время безотказной работы (средняя наработка на отказ) T0.
Вероятность безотказной работы P(t) есть вероятность того, что время работы системы до отказа окажется больше заданного времени t.
(1)
где Т – случайное время работы системы до отказа или наработка на отказ;
– интегральная функция распределения случайной величины Т (T < t).
Иногда пользуются понятием вероятности отказов Q(t):
(2)
Если P(t) – надежность системы, то Q(t) – ненадежность системы.
Плотность вероятности, или частота отказов, является дифференциальной функцией распределения.
(3)
Интенсивность отказа λ(t) – это отношение плотности вероятности к вероятности безотказной работы:
,
(4)
откуда
если
λ
= const,
(5)
Среднее время безотказной работы системы – это математическое ожидание времени работы системы до отказа:
Пределы несобственного интеграла изменяются от 0 до ∞, так как время не может быть отрицательным.
Интегрируем по частям, получим
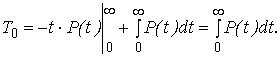(6)
,
так как при верхнем пределе P(t)
быстрее стремится к нулю, чем t
стремится к бесконечности.
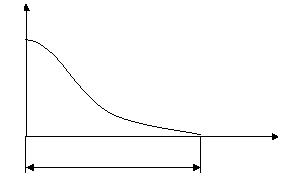
На рис. 3.1 изображена зависимость вероятности безотказной работы от времени. В начальный момент вероятность Р равна единице. В конце времени работы системы Т вероятность равна нулю.
Показатели надежности функционально связаны между собой: зная одну из функций P(t), Q(t), f(t), λ(t), можно определить три остальные.
Надежность систем с мгновенным восстановлением (показатели, методы расчета)
Для восстанавливаемых систем характерно чередование времени исправной работы и времени восстановления (ремонтов).
Система, проработав случайное время tp1, выходит из строя. После отказа происходит восстановление, и система работает вновь время tp2 до отказа. Этот процесс продолжается неограниченно. Полагаем, что время восстановления пренебрежимо мало по сравнению со временем работы. Можно считать, что восстановление происходит мгновенно. Отказавший, испорченный элемент немедленно заменяется новым. Элемент после восстановления имеет такую же надежность, что и в начальный момент.
Пусть интервалы времени безотказной работы между двумя соседними отказами распределены по экспоненциальному закону. Тогда вероятность того, что за промежуток времени t в системе произойдет n отказов, определится по формуле Пуассона:
,
(n
= 0, 1, 2, 3, …),
где λ – среднее число отказов в единицу времени или интенсивность отказов, λ = const;
λ = Λ, где Λ – параметр потока отказов. Этот параметр определяется по статистической формуле:
,
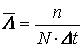(12)
где N – общее число отказавших элементов, или число восстановлений, остается неизменным. Отказавшие элементы заменяются новыми.
Поток отказов восстанавливаемой системы является простейшим, пуассоновским.
Параметром потока
отказов называется отношение числа
отказавших изделий в единицу времени
к числу испытываемых изделий при условии,
что все вышедшие из строя изделия
заменяются исправными (новыми или
отремонтированными) Согласно определению
,где
–
число отказавших образцов в интервале
времени от
до
;
N – число испытываемых образцов;
–
интервал времени.
Для простейшего потока параметр потока отказов определяются по формуле:
.
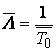Для ремонтируемых объектов удобным для практики критерием надежности является среднее время работы между двумя соседними отказами или наработка на отказ Т0.
Значения этого параметра определяются по результатам обработки статистического материала, полученного в ходе эксплуатации или экспериментов.
Если устройство проработало суммарное время t∑ и имело при этом n отказов в работе, то наработка на отказ
.
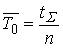(13)
Если испытывались N однотипных объектов, то необходимо просуммировать время исправной работы по всем объектам и разделить его на общее число отказов:
.
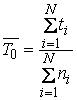(14)