8. Законы распределения отказов и их основные характеристики

Рассмотрим законы распределения случайной величины Т, где Т - время безотказной работы изделия до первого отказа (время наработки на отказ).

Экспоненциальный закон надёжности.

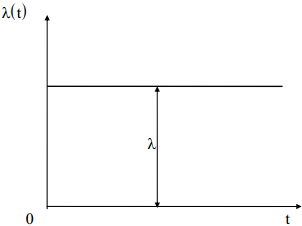
При экспоненциальном законе распределения времени безотказной Т интенсивность отказов является постоянной, т.е. .

Экспоненциальный закон надёжности справедлив для описания внезапных отказов, когда изделие не успевает ещё износиться, т.е. не стареет.

Для экспоненциального закона вероятность безотказной работы на каком-то интервале времени τ не зависит от прошедшего времени, а зависит от τ.

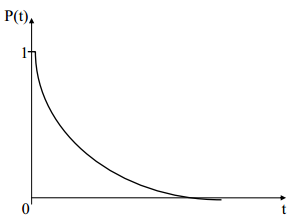
Формулы, по которым определяются количественные характеристики надёжности.

; ; ;

;

;

Здесь P (t,t₁) - вероятность безотказной работы изделия на интервале времени (t, t₁) при условии, что на интервале времени (0, t) изделие работало безотказно.

Нормальный закон распределения.

Он характеризует вероятность отказа при длительном изменении характеристик изделия (старение, износ). Нормальный закон распределения характеризует распределение времени безотказной работы изделия при возникновении отказов из-за износа и старения.

Плотность распределения времени безотказной работы Т изделия равна:

,

где m_t – среднее значение случайной величины T;

D_t - дисперсия случайной величины Т.

Для нормального закона распределения:

; ; ;

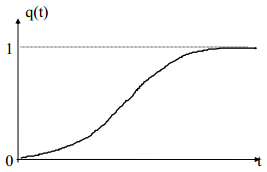
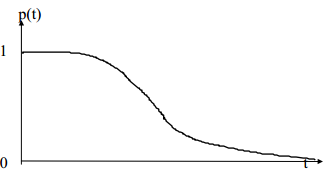
Определим вероятность безотказной работы изделия в интервале времени (t, t₁):

Определим интенсивность отказов λ(t) Имеем:

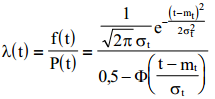
Определим P (t,t₁) - время безотказной работы изделия на интервале времени (t,t₁) при условии, что на интервале времени (0,t) изделие работало безотказно. Имеем:

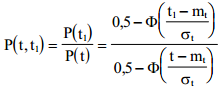
Закон распределения Вейбулла.

Для распределения Вейбулла плотность распределения времени безотказной работы Т изделия имеет вид:

;

здесь а и k - параметры закона распределения Вейбулла.

; ; ;

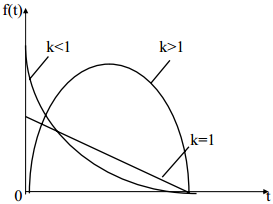
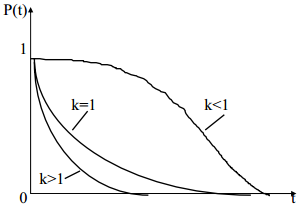
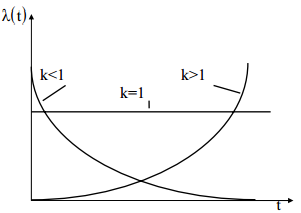
Среднее время безотказной работы:

; - гамма-функция;

Дисперсия времени безотказной работы T:

Рассмотрим случай, когда k=1, a= λ.

В этом случае имеем f(t) = λ .

Т.е. в этом случае имеем экспоненциальный закон надёжности.

Пусть k=2. В этом случае имеем закон Рэлея. Закон Вейбулла лучше описывает время безотказной работы изделия, чем экспоненциальный закон, т.к. в этом случае имеется два параметра: a и k.Пусть k=2, . Тогда имеем .

- закон распределения Релея.

;

;

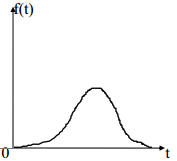
9. Экспоненциальный закон распределения надежности

Экспоненциальный закон.

где P(x) это вероятность того что Случайная величина (СВ) X имеет значение большее x.

В частном случае, когда за СВ принимается время работы системы t вероятность т ого что система на протяжении времени t будет находится в работоспособном состоянии будем равно:  .

где  l - интенсивность отказов системы. l – const.

Это выражение можно получить из закона Пуассона, если число отказов n = 0.

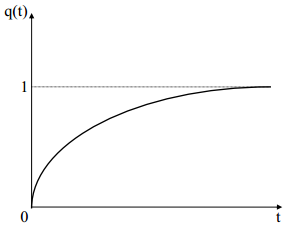
Вероятность отказа за время t м.б. записана Q(t) = 1 – P(t) = 1 - 

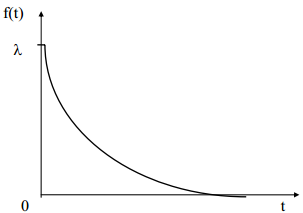
Плотность вероятности отказов F(t) = dQ / dt = l

Среднее время работы до возникновения отказа

Дисперсия – это время работы до возникновения отказа D(t) = 

Среднеквадратичное отклонение

Равенство   и Т₁ является характерным признаком экспоненциального распределения.