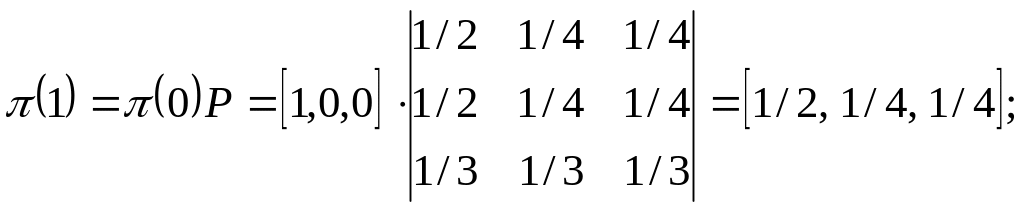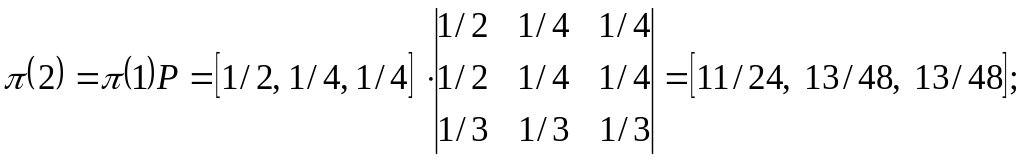Задачи к билету №1.

Задача 1. При тестировании программ в течение 100 часов было обнаружено 24 ошибки из них 8 искусственно внесённых, общее количество искусственно внесённых ошибок равно 20. Определить первоначальное число ошибок в программе. Определить вероятность того, насколько правильно найдено первоначальное число ошибок в программе.

Дано:	Решение: 1) Первоначальное число ошибок в программе найдём из формулы: 2) Вероятность того, насколько правильно найдено первоначальное число ошибок в программе, определим по следующей формуле: , т.к. k – количество собственных ошибок, а n – количество обнаруженных собственных ошибок, следовательно , тогда получаем: Ответ: 1) 2)
Найти: 1) 2)

Задача 2. Элемент имеет экспоненциальные законы распределения времени работы до отказа и времени восстановления с параметрами соответственно и . Вычислить все возможные параметры надёжности элемента через 100 часов его эксплуатации.

Дано:

Решение: 1) Вероятность безотказной работы рассчитаем по следующей формуле: 2) Вероятность отказа за время 100 часов рассчитаем по следующей формуле: 3) Среднее время наработки до отказа: 4) Среднее время восстановления рассчитываем следующим образом: 5) Коэффициент готовности рассчитывается по формуле: 6) Коэффициент оперативной готовности рассчитаем по формуле: . 7) Частота отказов изделия или плотность вероятности времени безотказной работы изделия при экспоненциальном законе распределения вычисляется по формуле: Ответ: 1) 2) 3) 4) 5) 6) 7)

Найти: 1) 2) 3) 4) 5) 6) 7)

Задача 3. Дана матрица вероятностей переходов. Определить вероятность нахождения системы в 3 состоянии после двух переходов, если изначально система находилась в первом состоянии с вероятностью равной 1.

Дано:	Решение: 1) Вероятность пребывания системы в том или ином состоянии после 1 перехода: 2) Вероятность пребывания системы в том или ином состоянии после 2 переходов: Ответ:
Найти: 1) 2)

Задача 4. Чему равна кратность резерва, если для основного элемента предусмотрен следующий резерв: один элемент, работающий в том же режиме, что и основной, один элемент работающий в облегченном режиме и ещё один элемент, находящийся в ненагруженном состоянии.

Дано:	Решение: Кратность резерва определим по формуле: Ответ:
Найти:

Задача №1.

При тестировании программы в течение 80 часов было обнаружено 32 ошибки. Из них 8 искусственно внесенных. Общее количество искусственно внесенных ошибок равно 40. Определить первоначальное число ошибок в программе. Определить вероятность того, насколько правильно найдено первоначальное число.

Решение

Воспользуемся статистической моделью Миллса.

Таким образом,

Вероятность того, насколько правильно найдено первоначальной число ошибок:

, где

- мера доверия к модели, которая показывает насколько правильно найдено значение N;

- число найденных собственных ошибок;

- первоначальное число собственных ошибок;

- число внесенных искусственных ошибок.

Таким образом,

.

Ответ: 120 ошибок, вероятность правильность результатов составляет 24,8%.

Задача №2

Элемент имеет экспоненциальный закон распределения времени работы до отказа и времени восстановления с параметрами соответственно =0,08 1/час и =1 1/час. Вычислить все возможные параметры надежности элемента через 50 часов его эксплуатации.

Решение

• ВБР

, начальное состояние – работоспособное.

• Вероятность отказа

• Среднюю наработку до отказа;

• Среднее время восстановления;

• Коэффициент готовности.

• Коэффициент оперативной готовности

Задача 3

Дана матрица вероятностей переходов. Определить вероятность нахождения в 3 состоянии после двух переходов, используя любой из известных Вам методов. Предполагаем, что изначально система с вероятностью 1 находилось в первом состоянии.

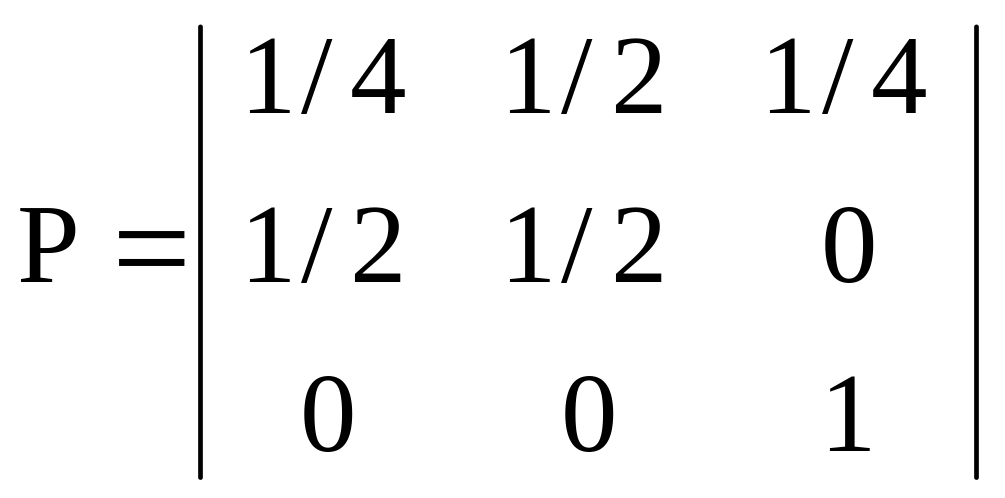
Какова вероятность, что процесс закончится в поглощающем состоянии?

Решение:

Система в начальный момент времени находилась в первом состоянии с вероятностью 1:

Вероятность пребывания системы в том или ином состоянии после 1 перехода:

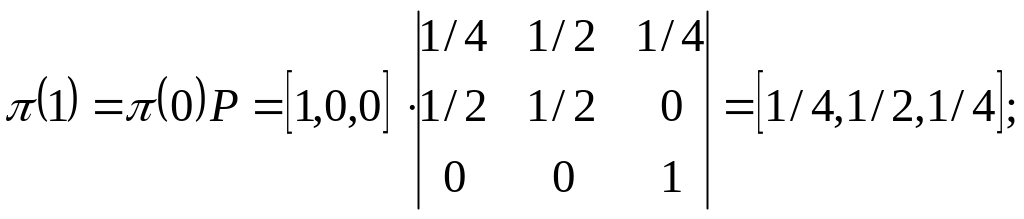
Вероятность пребывания системы в том или ином состоянии после 2 перехода:

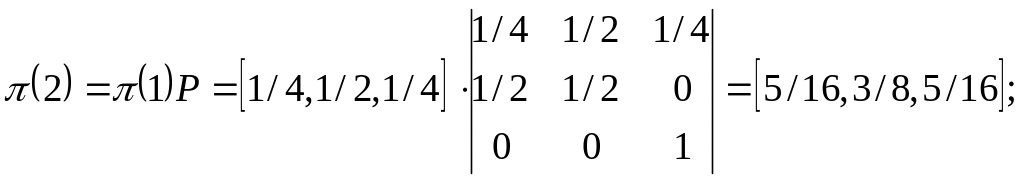
Определение вероятности, в случае, если процесс закончится в поглощающем состоянии:

Из матрицы переходов P вычеркиваются строки и столбцы с индексом поглощающего состояния и получают матрицу Q.

В данном случае 2 поглощающих состояния: 2 и 3 состояния.

Таким образом, имеем:

Среднее число попаданий процесса из состояния в состояние равно:

,

где - единичная матрица.

В таком случае имеет вид:

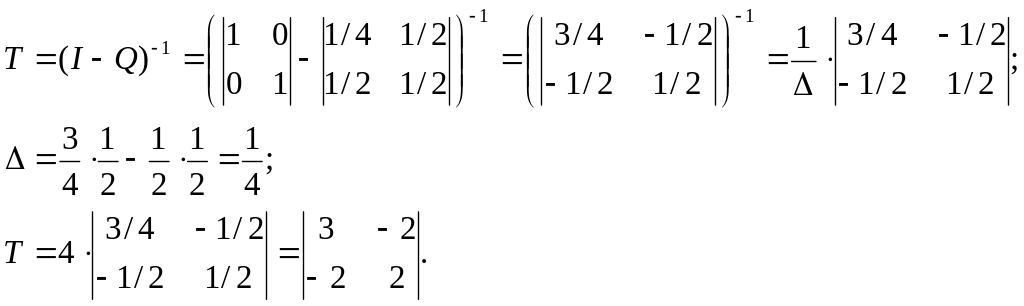
Среднее число шагов, которое требуется для перехода процесса из не поглощающего состояния в какое-нибудь поглощающее равно:

,

где - вектор-столбец, все компоненты которого равны 1.

Таким образом:

Вероятность того, что процесс завершится переходом в данное поглощающее состояние равно:

,

где - матрица, получаемая из матрицы вероятностей перехода вычеркиванием отвечающих поглощающим состояниям строк и не поглощающим состоянием столбцов.

.

Тогда вероятность равна:

Ответ:

Задача 4

Построить граф переходов и матрицу переходных вероятностей для системы состоящей из одного рабочего элемента и 2 резервных. Один из резервных элементов не нагружен, другой – частично нагружен. Интенсивность отказа каждого элемента =0,08 1/час. Коэффициент загрузки ненагруженного резерва 0,3. Восстановление элементов осуществляется одним ремонтным органом =1 1/час.

Позже…