Билет №34. Дифференциал и его геометрическое значение.

1.Дифференциалом функции называется произведение производной на приращение независимой переменной

dy=f'(x)*Δx

Дифференциал независимой переменной равен приращению этой переменной =>

dy=f'(x)*dx или f'(x)=dy/dx

^{Пример. Найти дифференциал функции f(x)=x3}

d(x3)=(x3)dx=3x2dx

2.Дифференциал функции равен приращению ординаты касательной, проведенной к графику в точке (х;у) при изменении x на велечину Δx=dx

Билет №35.

Пусть y = f(x) является дифференцируемой функцией. Тогда производная также представляет собой функцию от x. Если она является дифференцируемой функцией, то мы можем найти вторую производную функции f, которая обозначается в виде

f''=(f')'=(dy/dx)=d/dx(dy/dx)=d2y/dx2

Аналогично, если f '' существует и дифференцируема, мы можем вычислить третью производную функции f:

f'''=(f'')'=d3y/dx3

Производные более высокого порядка (если они существуют), определяются как

f''''=(f''')'=d4y/dx4

Д ля нахождения производных высшего порядка можно использовать следующие формулы

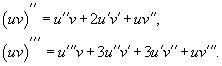
Пример.

Найти y'', если .

y(x)=x*ln(x)

Решение. Возьмем первую производную дифференцируя функцию как произведение.

Теперь найдем производную второго порядка

Билет №36. Знак производной на интервале и монотонность функции ( с выводом из теоремы Лагранжа).

Знак производной на интервале

Функция         имеет максимум в точке        , если её значение в этой точке больше, чем её значения во всех точках некоторой окрестности, содержащей точку      . Функция         имеет минимум в точке        , если её значение в этой точке меньше, чем её значения во всех точках некоторой окрестности, содержащей точку     . Для определения критических точек находим производную по соответствующим правилам и используя таблицу производных. В критических точках производная равна нулю или не существует. Определяем знак производной в интервалах между критическими точками. Если на некотором интервале производная положительна, то функция возрастает. Если производная отрицательна, то на данном интервале функция убывает.

Монотонность функции

Определение 1: Функции называется возрастающей [убывающей] на множестве , если для любых значений аргумента из выполняется условие .

Определение 2.Промежутки, на которых функция возрастает (убывает) называются промежутками монотонности функции .

Определение 3: Функция называется возрастающей [убывающей], если для любых значений аргумента из выполняется условие .

Определение 4: Возрастающие и убывающие функции называются монотонными.

• Свойство 1. Пусть функция возрастает (убывает) на множестве и С – любое число. Тогда функция , также возрастает (убывает) на множестве .

• Свойство 2. Пусть функция возрастает (убывает) на множестве и C > 0. Тогда функция , также возрастает (убывает) на множестве .

• Свойство 3. Пусть функция возрастает (убывает) на множестве и C < 0. Тогда функция , убывает (возрастает) на множестве .

• Свойство 4. Пусть функция возрастает (убывает) и знакопостоянна на множестве . Тогда функция , убывает (возрастает) на множестве .

• Свойство 5. Сумма возрастающих (убывающих) функций есть функция возрастающая (убывающая).

• Свойство 6. Произведение возрастающих (убывающих) неотрицательных функций есть функция возрастающая (убывающая).

Теорема 1. Если функция возрастает на множестве , а функция убывает на множестве , то уравнение имеет на не более одного корня.

Теорема 2. Если функция монотонна на множестве , а функция постоянна на множестве , то уравнение имеет на не более одного корня.

Билет 37. Производная второго порядка, графический смысл ее знака на интервале.

Производная второго порядка

Если функция дифференцируема, то ее производную называют второй производной от f и обозначают :

Вторая производная от параметрической функции x = x (t) и y = y (t) задается формулой:

Вторую производную иногда обозначают:

Вторая производная определяет скорость изменения скорости или ускорение.

Дважды дифференцируемая на [a; b] функция f (x) выпукла вверх, если для любого

Дважды дифференцируемая на [a; b] функция f (x) выпукла вниз, если для любого

Билет №38. Отыскание асимптот функции. Пример, показывающий, что могут быть разные асимптоты при x→+∞ и x→-∞.

Асимптота – прямая, к которой приближаются точки графика функции при бесконечном удалении их от начала координат. Асимптота может быть вертикальной или наклонной. Вертикальная А. имеет уравнение x=b , причем f(x)→+∞ (-∞) при x→a (односторонне).

Пусть функция f (x) определена для всех x. Если существуют такие числа k и b, что f(x)-kx-b = 0 при х, то прямая y = kx + b называется наклонной асимптотой графика функции f (x).

k = lim f(x)/x при x→+∞ (x→-∞)

b = lim (f(x)-kx) при x→+∞ (x→-∞)

Пример разных асимптот на разных бесконечностях:

y=

x→+∞ k = lim = lim = 1 b=0

x→-∞ k = lim = lim = -1 b=0

Билет №39. План исследования функции для построения ее графика. Пример: и построить ее график.

1. Найти область определения функции

x∈(-∞;1) ∪(1; +∞)

2. Определить, является ли функция четной, нечетной или общего вида

Не обладает четностью

3. Определить нули и промежутки знакопостоянства функции

- + + x

0 1

4) Выяснить поведение функции на границе области определения, т.е. найти односторонние пределы в точках, не принадлежащих к области определения

x→1+0

x→1-0

5)Выяснить поведение функции на бесконечности

x→+∞ x→-∞

6)Найти наклонные асимптоты – по отдельности для x→+∞ и x→-∞, или убедиться в их отсутствии

y=kx+b

x→+∞ x→-∞

x→-∞ x→-∞

y=x+2

7. Найти первую производную, определить критические точки и промежутки знакопостоянства первой производной. Определить промежутки возрастания и убывания функции, а также точки экстремума.