5.2. Аппроксимация переходной характеристики

Далее решается задача определения коэффициентов передаточной функции (дифференциального уравнения) по графику переходной функции. Существует несколько методов решения этой задачи.

5.2.1. Аппроксимация переходных характеристик объектов с

самовыравниванием характеристикой апериодического звена

первого порядка с запаздыванием

Часто в инженерных расчетах объекты с самовыравниванием аппроксимируются достаточно простой характеристикой цепочки апериодического звена первого порядка и звена чистого запаздывания. Следовательно, аппроксимирующая передаточная функция будет иметь следующий вид:

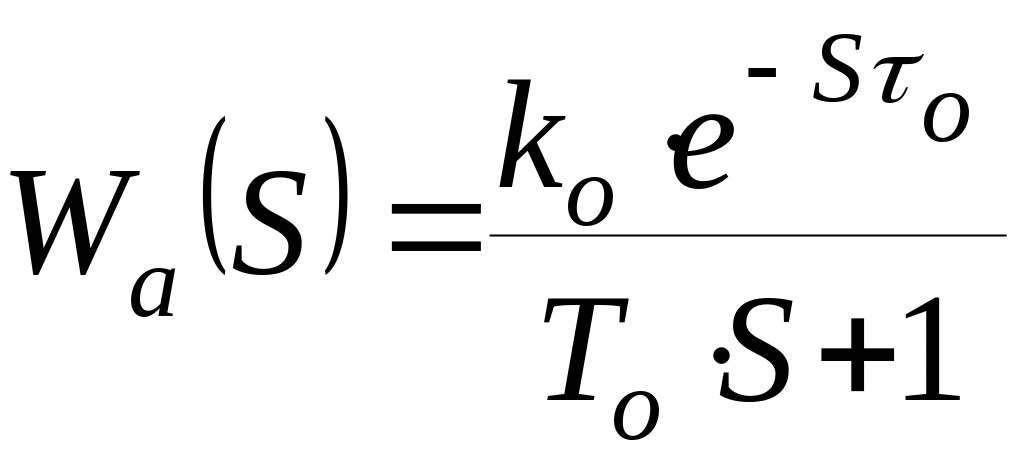, (2)

где k_О - коэффициент усиления объекта, [мВ/мВ]

Т_О - постоянная времени объекта, [c]

_О - время транспортного запаздывания объекта, [с].

Для определения коэффициентов передаточной функции (k_О, Т_О, _О) на графике переходной характеристики проводят касательную в точке перегиба (приближенно) (рис. 2).

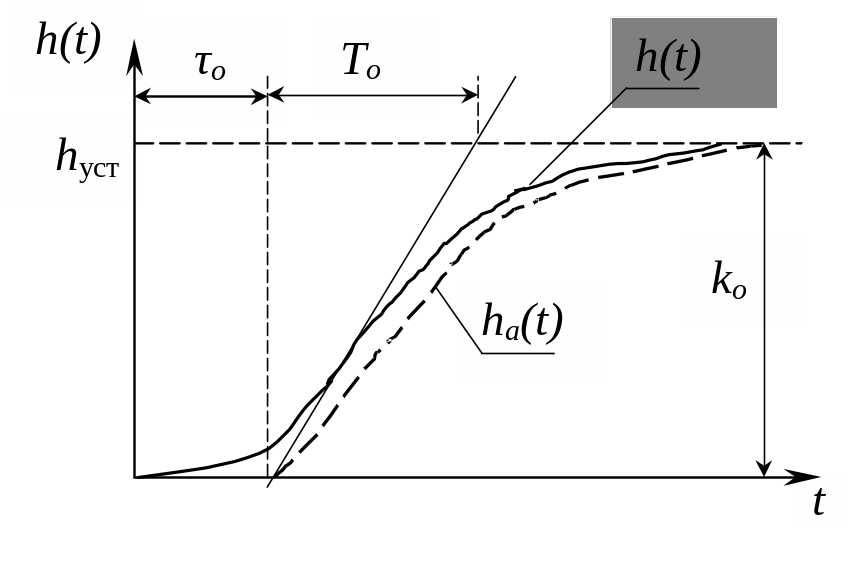
Рис.2. Переходная характеристика h(t) объекта с самовыравниванием

Коэффициент усиления объекта определяется как , т.е. k_о=h_УСТ, где h_УСТ - новое установившееся значение выходной величины. Постоянная времени T_О определяется наклоном касательной и равна отрезку, отсекаемому ею при пересечении с осью абсцисс (старое равновесное состояние) и с прямой, определяющей уровень нового установившегося значения выходной величины. Отрезок же от начала координат до точки пересечения касательной с осью абсцисс равен времени транспортного запаздывания _О.

Выражение для аппроксимирующей переходной характеристики h_А(t) можно определить по следующей формуле:

, (3)

где L^-1 - знак обратного преобразование Лапласа.

Подставив в формулу (3) выражение (2) после необходимых преобразований получим:

(4)

Подставив в выражение (4) найденные параметры k_О, T_О и _О, построим график аппроксимирующей переходной функции в той же системе координат, что и исходный график h(t) (рис. 2).

5.2.2. Аппроксимация переходных характеристик объектов с

самовыравниванием "по трем точкам"

Особенности этого метода [2] заключаются в следующем:

1) Исходные данные об объекте задаются в виде графика его переходной характеристики h(t) (рис. 3).

2) Аппроксимирующую передаточную функцию ищут в виде:

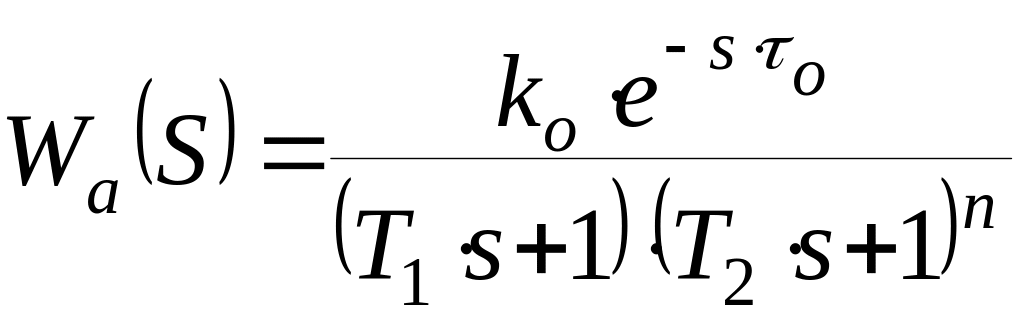. (5)

3) Критерием приближения является требование совпадения аппроксимируемой h(t) и аппроксимирующей h_А(t) характеристик в точках t = 0, t =  и в точке перегиба t_П, определяемой из условия:

. (6)

Кроме того, в точке перегиба эти характеристики должны иметь одинаковый наклон . Таким образом, критерий приближения имеет следующий вид:

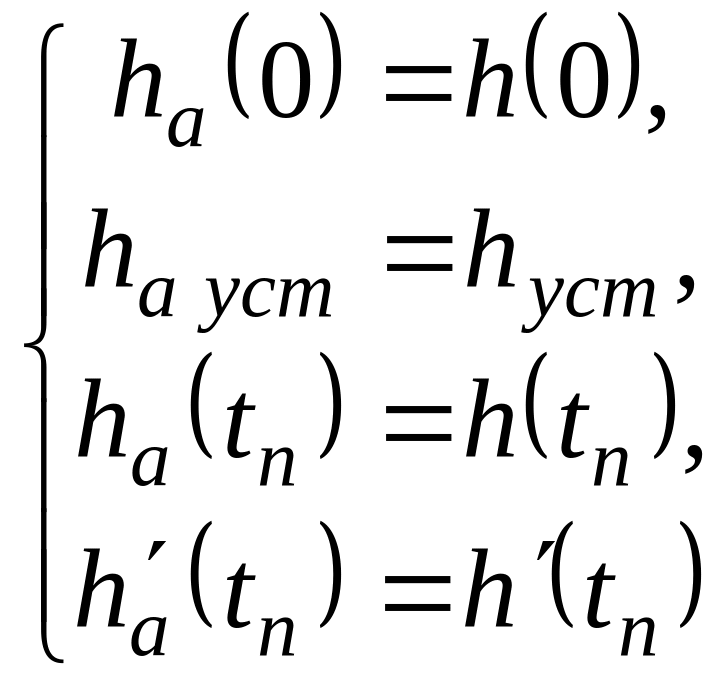(7)

Для определения производной переходной характеристики h(t) в точке, где эта характеристика имеет максимальный наклон, проводится касательная и определяется длина отрезка Т₀, заключенного между точками пересечения этой касательной с осью абсцисс и линией установившегося значения характеристики h_УСТ. Примем обозначение:

b = h (t_П) / h_УСТ . (8)

Рассмотрим модель, состоящую из двух апериодических звеньев первого порядка с запаздыванием (n=1):

(9)

Здесь k = h_УСТ, а переходная характеристика модели без учета запаздывания определяется формулой:

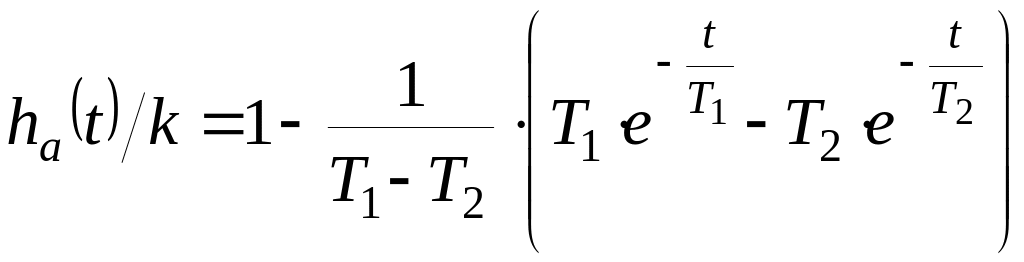(10)

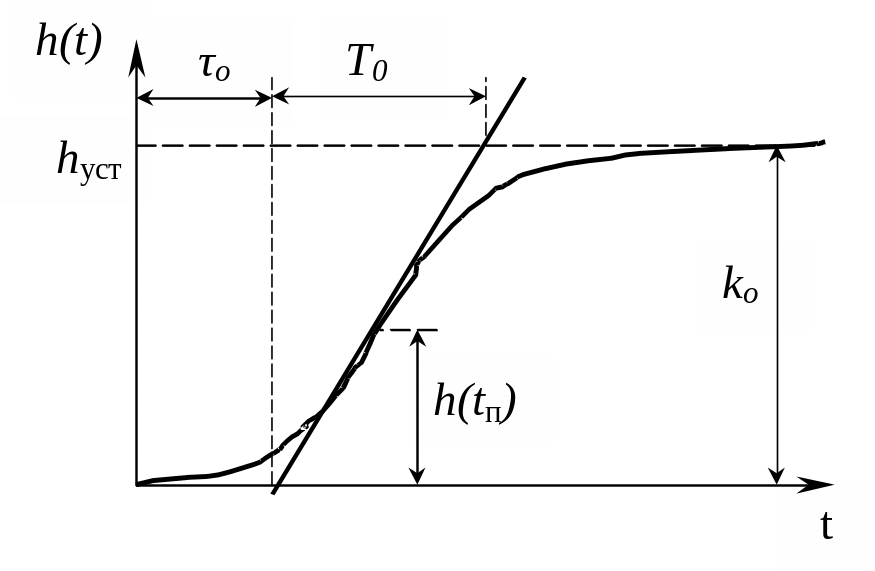
Рис.3. График переходной характеристики h(t) объекта

Для определения параметров передаточной функции (9) необходимо воспользоваться номограммой (рис. 4):

• рассчитать коэффициент b по формуле (8), используя переходную характеристику;

• на оси b отложить полученное значение и провести горизонтальную прямую до пересечения с жирной линией (b) с обозначением n=1 и отметить точку пересечения (в случае получения значения коэффициента b более 0.275 точнее определить координаты точки перегиба);

• провести вертикальную прямую и считать по горизонтальной шкале значение соотношения Т₂/Т₁, а также отметить точки пересечения с кривыми (Т₁/Т₀) и (t_П.А./Т₁) для n=1;

• от точек пересечения провести горизонтальные прямые и считать по соответствующим шкалам величины соотношений Т₁/Т₀ и t_П.А./Т₁;

• по графику переходной характеристики (рис. 3) определить параметр Т₀ и рассчитать из соотношений t_П.А. ,Т₁ ,Т₂ .

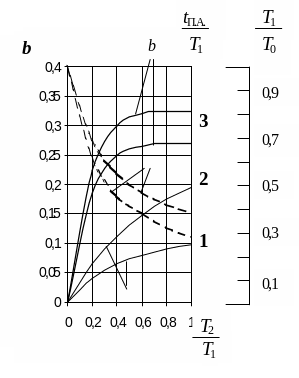
Рис.4. Номограмма для определения отношений T₁/T_o, T₂/T₁, t_П.А./T₁.

Если найденное значение t_П.А. будет меньше t_П, определенного по графику h(t), определить время запаздывания как:

z = t_П - t_П.А. (11)

В итоге получить выражение для передаточной функции объекта W(S).