
Глава 9. Дифференциальные и разностные уравнения.
§1. Обыкновенные дифференциальные уравнения
первого порядка.
В задачах 9.1-9.12 найти общие решения следующих ДУ с разделяющимися переменными:
9.1 .
9.2
.
9.2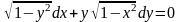 .
.
9.3
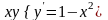 .
9.4
.
9.4
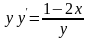 .
.
9.5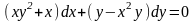 .
9.6
.
9.6 .
.
9.7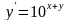 .
9.8
.
9.8
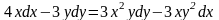 .
9.9
.
9.9
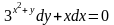 .
9.10
.
9.10
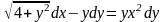 .
.
9.11
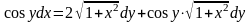 .
.
9.12
 .
.
Дифференциальное
уравнение вида
 (
(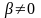 )
приводится к уравнению с разделяющимися
переменными подстановкой
)
приводится к уравнению с разделяющимися
переменными подстановкой
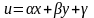 ,
где
,
где
 -
новая искомая функция.
-
новая искомая функция.
В задачах 9.13-9.16 найти общие решения уравнений, приводящихся к ДУ с разделяющимися переменными:
9.13
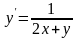 .
9.14
.
9.14
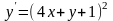 .
.
9.15
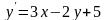 .
9.16
.
9.16
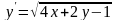 .
.
В задачах 9.17-9.22 найти частные решения ДУ, удовлетворяющие указанным начальным условиям:
9.17
 ,
,
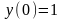 .
.
9.18
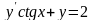 ,
,
 .
.
9.19
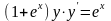 ,
.
,
.
9.20
 ,
,
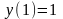 .
.
9.21
 ,
,
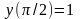 .
.
9.22
 ,
,
 .
.
9.23
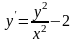 .
9.24
.
9.24
 .
.
9.25
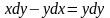 .
9.26
.
9.26
 .
.
9.27
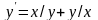 .
9.28
.
9.28
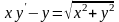 .
.
9.29
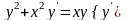 .
9.30
.
9.30 .
9.31
.
9.31
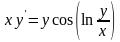 .
9.32
.
9.32
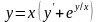 .
.
9.33
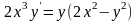 .
9.34
.
9.34
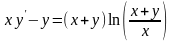 .
.
9.35 .
9.36
.
9.36 .
.
В задачах 9. 37-9.40 найти общие решения уравнений:
9.37
 .
9.38
.
9.38
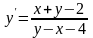 .
.
9.39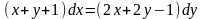 .
.
9.40
 .
.
В задачах 9.41-9.46 найти частные решения уравнений, удовлетворяющие указанным начальным условиям:
9.41
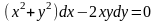 ,
,
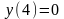 .
.
9.42
 ,
.
,
.
9.43
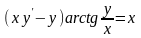 ,
.
9.44
,
.
9.44
 ,
,
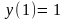 .
.
9.45
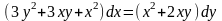 ,
.
,
.
9.46
 ,
.
,
.
9.51
 .
9.52
.
9.52
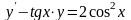 .
.
9.53
 .
9.54
.
9.54
 .
.
9.55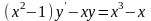 .
9.56
.
9.56
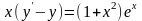 .
.
9.57
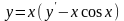 .
9.58
.
9.58
 .
.
9.59
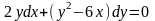 .
9.60
.
9.60
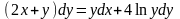
9.61
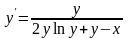 .
9.62
.
9.62
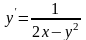 .
.
В задачах 9.63-9.70 найти частные решения уравнений, удовлетворяющие указанным начальным условиям:
9.63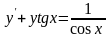 ,
,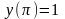 .
9.64
.
9.64
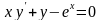 ,
,
 .
.
9.65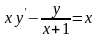 ,
.
9.66
,
.
9.66 ,
,
 .
.
9.67 ,
.
,
.
9.68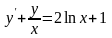 ,
.
9.69
,
.
9.69
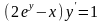 ,
,
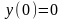 .
.
9.70
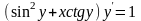 ,
,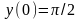 .
.
В задачах 9.47-9.62 найти общие решения следующих линейных дифференциальных уравнений:
9.47
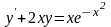 .
9.48
.
9.48
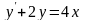 .
.
9.49
 .
9.50
.
9.50
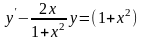 .
.
В задачах 9.71-9.78 найти общие решения уравнений Бернулли:
9.71
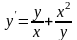 .
9.72
.
9.72
 .
.
9.73
 .
9.74
.
9.74
 .
.
9.75
 .
9.76
.
9.76
 .
.
9.77
 .
9.78
.
9.78
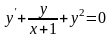 .
.
В задачах 9.79-9.86 решить следующие уравнения, предварительно убедившись, что они являются уравнениями в полных дифференциалах:
9.79
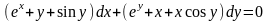 .
.
9.80
 .
.
9.81
 .
9.82
.
9.82
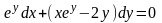 .
.
9.83
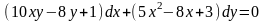 .
.
9.84
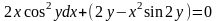 .
.
9.85
 ;
;
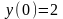 .
.
9.86
 ;
.
;
.
В
задачах 9.87-9.92 разрешить
следующие уравнения относительно
 и найти их
общее решение:
и найти их
общее решение:
9.87
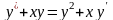 . 9.88
. 9.88
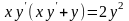 .
.
9.89
 .
9.90
.
9.90
 .
.
9.91
 .
9.92
.
9.92
 .
.
В задачах 9.93-9.98 найти общие решения следующих уравнений методом введения параметра:
9.93
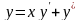 .
9.94
.
9.94
 .
.
9.95
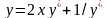 .
9.96
.
9.96
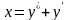 .
.
9.97
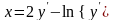 .
9.98
.
9.98
 .
.
В задачах 9.99-9.120 найти общие решения следующих дифференциальных уравнений первого порядка:
9.99
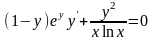 .
9.100
.
9.100
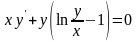 .
.
9.101
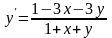 .
9.102
.
9.102
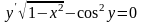 .
.
9.103
 .
9.104
.
9.104
 .
.
9.105
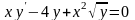 .
9.106
.
9.106
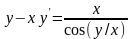 .
.
9.107
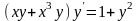 .
9.108
.
9.108 .
.
9.109
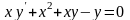 .
9.110
.
9.110
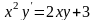 .
.
9.111
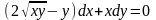 .
9.112
.
9.112
 .
.
9.113
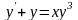 .
9.114
.
9.114
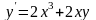 .
.
9.115
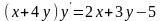 .
9.116
.
9.116
 .
.
9.117
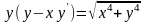 .
9.118
.
9.118
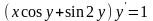 .
.
9.119
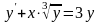 .
9.120
.
9.120
 .
.
В задачах 9.121-9.128 найти решения, предварительно составив дифференциальное уравнение.
9.121 Найти кривые, у которых точка пересечения любой касательной с осью абсцисс имеет абсциссу, вдвое меньшую абсциссы точки касания.
9.122
Найти кривые,
у которых площадь треугольника,
ограниченного касательной, осью абсцисс
и отрезком от начала координат до точки
касания, есть величина постоянная,
равная
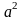 .
.
9.123
Найти
атмосферное давление на высоте
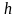 ,
если на поверхности Земли давление
равно
,
если на поверхности Земли давление
равно
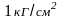 и плотность воздуха
и плотность воздуха
 (Указание:
использовать
закон Бойля-Мариотта, согласно которого
плотность пропорциональна давлению).
(Указание:
использовать
закон Бойля-Мариотта, согласно которого
плотность пропорциональна давлению).
9.124
Тело охладилось за 10 мин от
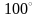 С
до
С
до
 С.
Температура окружающего воздуха
поддерживается равной
С.
Температура окружающего воздуха
поддерживается равной
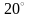 С.
Когда тело остынет до
С.
Когда тело остынет до
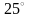 С?
(Указание:
принять, что
скорость остывания тела пропорциональна
разности температур тела и окружающей
среды).
С?
(Указание:
принять, что
скорость остывания тела пропорциональна
разности температур тела и окружающей
среды).
9.125
На материальную
точку массы
 действует постоянная сила, сообщающая
точке ускорение
действует постоянная сила, сообщающая
точке ускорение
 .
Окружающая среда оказывает движущейся
точке сопротивление, пропорциональное
скорости её движения, коэффициент
пропорциональности равен
.
Окружающая среда оказывает движущейся
точке сопротивление, пропорциональное
скорости её движения, коэффициент
пропорциональности равен
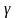 .
Как изменяется скорость движения со
временем, если в начальный момент точка
находилась в покое? (Указание:
воспользоваться вторым законом Ньютона
.
Как изменяется скорость движения со
временем, если в начальный момент точка
находилась в покое? (Указание:
воспользоваться вторым законом Ньютона
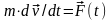 ).
).
9.126
Материальная
точка движется по прямой со скоростью,
обратно пропорциональной пройденному
пути. В начальный момент точка находилась
на расстоянии
 от начала отсчёта пути и имела скорость
от начала отсчёта пути и имела скорость
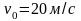 .
Определить пройденный путь и скорость
точки через
.
Определить пройденный путь и скорость
точки через
 секунд
после начала движения.
секунд
после начала движения.
9.127
Имеется
некоторое количество радиоактивного
вещества. Известно, что через
 дней
распадается 50% этого вещества. Через
сколько дней останется 1% начального
количества вещества? (Указание:
из эксперимента известно, что скорость
радиоактивного распада пропорциональна
количеству вещества).
дней
распадается 50% этого вещества. Через
сколько дней останется 1% начального
количества вещества? (Указание:
из эксперимента известно, что скорость
радиоактивного распада пропорциональна
количеству вещества).
9.128
Скорость
обесценивания оборудования вследствие
его износа пропорциональна в каждый
момент времени его фактической стоимости
 .
Начальная стоимость оборудования равна
.
Начальная стоимость оборудования равна
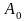 .
Найти стоимость оборудования по истечении
.
Найти стоимость оборудования по истечении
 лет.
лет.
9.129
Численность
населения
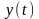 некоторого города удовлетворяет
уравнению
некоторого города удовлетворяет
уравнению
 ,
где
-время
(в годах). В начальный момент население
города составляло 10 тысяч человек. Через
сколько лет население увеличится в 10
раз?
,
где
-время
(в годах). В начальный момент население
города составляло 10 тысяч человек. Через
сколько лет население увеличится в 10
раз?
9.130
Функции
спроса
 и
предложения
и
предложения
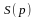 на некоторый товар имеют вид:
на некоторый товар имеют вид:
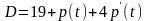 и
и
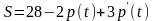 .
Найти зависимость равновесной цены от
времени
,
если в начальный момент времени цена
.
Найти зависимость равновесной цены от
времени
,
если в начальный момент времени цена
 ден.ед.
ден.ед.
