4. Расчет и выбор посадок колец подшипников качения

Сопряжение вала 29 и шарикового радиального подшипника 31 в корпусе.

D₁₅=35 мм;

R=9 кН;

серия подшипника 407 [3] табл.П.3.1

Радиальный зазор:

-наибольший: 0,02 мм

-наименьший: 0,012 мм [4 ] прил. 7, ст. 197.

Определяем по соответствующим стандартам основные размеры заданного подшипника:

d=35 мм

D=100 мм

B=25 мм

r=2,5 мм [6] с. 118, табл. 1.

Рисунок 4.1 Присоединительные размеры подшипника

4.1 Выбор класса точности подшипника и предельных отклонений сопрягаемых поверхностей

В зависимости от точности изготовления и сборки подшипников качения установлены следующие классы точности, указанные в порядке возрастания точности: 0, 6, 5, 4, 2 – для упорных и упорно-радиальных подшипников. Наиболее часто в машиностроении используют подшипники классов точности 0 и 6. Подшипники классов точности 5 и 4 применяются при большой частоте вращения.

Принимаем класс точности подшипника – 0, так как число оборотов в нашем червячно-цилиндрическом редукторе не большое.

.

4.2 Определение вида нагружения

Из анализа работы узла устанавливаем, что радиальная нагрузка на опору действует постоянно в одном направлении, при этом внутреннее кольцо должно вращаться вместе с валом во избежание износа поверхности вала и развальцовки сопрягаемой поверхности кольца.

Внешнее кольцо при этом установлено в корпусе неподвижно, следовательно, дорожка внешнего кольца поочередно нагружается действующей на опору силой в результате вращения его относительно постоянной по направлению нагрузки. Исходя из этого, делаем вывод: внутренне кольцо испытывает циркуляционный вид нагружения, а внешнее – местный.

4.3 Расчет и выбор посадки для внутреннего кольца

Рассчитываем посадку циркуляционно нагруженного внутреннего кольца подшипника на вал по интенсивности радиальной нагрузки на посадочной поверхности по формуле 4.25 [2]:

P_R= K_n· F· F_A (4.1)

где – радиальная реакция опоры на подшипник;

– рабочая ширина посадочного места ( );

K_n – динамический коэффициент посадки, зависящей от характера нагрузки;

– коэффициент, учитывающий степень ослабления посадочного натяга при полом вале или тонкостенном корпусе;

– коэффициент неравномерного распределения радиальной нагрузки между рядами тел качения.

b= B-2r=25-2·2,5= 20 мм

K_n=1 т.к. отсутствует перегрузка

F=1

F_A=1

P_R= ·1·1·1=450

По табл. 4.90.1 [2] заданным условиям для вала соответствует поле допуска k6. По полученному результату выбираем нормальный или легкий тип нагружения. По табл. 4.91 [2] рекомендуемая посадка:

Размерные параметры вала 35 k6 ( [2] табл. 1.29

Номинальный размер d_n=35 мм.

Верхнее предельное отклонение es= + 0,018мм.

Нижнее предельное отклонение ei= + 0,002мм.

Наибольший предельный размер d_max=d_n+es=35 + 0.018=35,018 мм. (4.2)

Наименьший предельный размер d_min=d_n+ei=35+0,002=35,002 мм. (4.3)

Допуск размера Td=d_max–d_min=35,018-35,002=0,016мм. (4.4)

Размерные параметры отверстия 35L0 .

Номинальный размер D_n=35мм.

Верхнее предельное отклонение ES=0мм.

Нижнее предельное отклонение EI= –0,012мм.

Наибольший предельный размер D_max=D_n+ES = 35мм (4.5)

Наименьший предельный размер D_min=D_n+EI=35–0,012=34,988мм. (4.6)

Допуск размера TD=D_max–D_min=35-34,988=0,012мм (4.7)

Определим характеристики сопряжения:

Наименьший зазор S_min=EI–es=–0,012 – 0.018= 0,006 мм. (4.8)

Наибольший зазор S_max=ES–ei=0 – 0,002= – 0,002 мм. (4.9)

Средний зазор S_с= мм (4.10)

Наименьший натяг N_min= 0,002 мм [2] табл. 4.92

Наибольший натяг N_max= 0,030 мм [2] табл. 4.92

Образованный натяг необходим для обеспечения неподвижности соединения кольца подшипника и сопряженной детали, т.к. поворот кольца приведет к истиранию поверхности детали.

Выбранную посадку во избежание разрыва кольца проверим по максимальному натягу:

[N]= = 0,1596 мм [3] с. 10 (4.11)

k=2,0 (для тяжелой серии подшипника)

[ = 400МПа – принимаем по рекомендациям [3] с.349.

N_max=0,03 мм ˂ [N]= 0,1596 мм

Проанализировав данные, получим, что > – условие выполнено.

Определяем величину посадочного радиального зазора:

∆_пос= - ∆_{деф. к} [3] с. 11 (4.11)

∆_пос =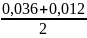 -0,01161=+0,01239 мм

∆_{деф. к}=0,85 N_max· = 0,85·0,02· = 0,01161 мм [3] с. 11 (4.12)

d₀=d+ = 35 + = 51,25 мм [3] с. 11 (4.13)

∆_{нач нб}=0,026 мм

∆_{нач наим}=0,012 мм _. приложение 7 [5]

∆_пос=+0,001239 мм ≥ ∆_{нач наим}=0,012 мм - условие выполняется