5. Гибель (рекомбинация) нейтральных и заряженных частиц. Л1(§1.4, в конце. Вся математика нужна!), лекции

Под рекомбинацией заряженных частиц понимают столкновение носителей противоположного знака, приводящее к их взаимной нейтрализации.( Гетерогенная рекомбинация (реакции частиц на стенках реактора) Доминирует в системах низкого давления)

Кинетика объемной (т. е. протекающей в объеме плазмы) рекомбинации заряженных частиц характеризуется коэффициентом α_R , который представляет собой коэффициент в уравнении

Предположив, n_n_−n и обозначив концентрацию при t = 0 через n₀ , решение уравнения можно получить в виде

Из последнего уравнения следует, что коэффициент рекомбинации можно найти, если известна скорость убыли числа носителей заряда в газе после прекращения ионизации. При рекомбинации двух противоположных зарядов их полная внутренняя энергия уменьшается, то есть процесс идет с выделением энергии. Так, например, в случае атомарных ионов величина выделившейся энергии равна разности энергий ионизации положительного иона и сродства к электрону отрицательного иона. В силу требований сохранения импульса и момента количества движения, переход энергии, выделяющейся при рекомбинации, в кинетическую энергию образующихся частиц почти невозможен. Поэтому рекомбинация заряженных частиц может протекать по одному из следующих механизмов: 1. С передачей энергии третьему телу:A⁺ +B^- +C→A+B+C^*. 2. С излучением кванта света:A⁺ +B^- →A+B+hν.3. С возбуждением образующихся частиц: A⁺ + B^- → A^* + B. 4.Диссоциативная рекомбинация: AB⁺ + C^- → A + B + C.

Под рекомбинацией нейтральных частиц понимают процессы взаимодействия свободных атомов и/или радикалов, приводящие к образованию стабильных молекул.( Гомогенная рекомбинация (реакции частиц в объеме плазмы) Доминирует в системах высокого давления)

Подобно рекомбинации заряженных частиц, такие процессы также идут с выделением энергии, поэтому механизмы рекомбинации обусловлены способностями системы диссипировать эту энергию. Основным механизмом объемной рекомбинации в условиях ННГП является трехчастичный процесс A B M →AB M , где третья частица ( M ) служит «приемником» избыточной энергии, стабилизируя образующуюся молекулу. Поскольку одновременное столкновение трех частиц при низких давлениях является маловероятным, предполагается, что данный процесс имеет комплексный характер:

Анализ формальной кинетики реакций показывает, что скорость образования стабильной молекулы АВ R_AB может быть найдена следующим образом:

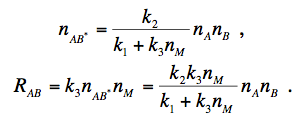В области высоких давлений в пределе имеем k₃n_M k₁ , поэтому выражение для R_AB преобразуется к виду R_AB k₂n_An_B . В области низких давлений k₃n_M k₁ , поэтому

что формально соответствует элементарному трехчастичному процессу ^k₄
(над стрелкой)ABM→ABM .

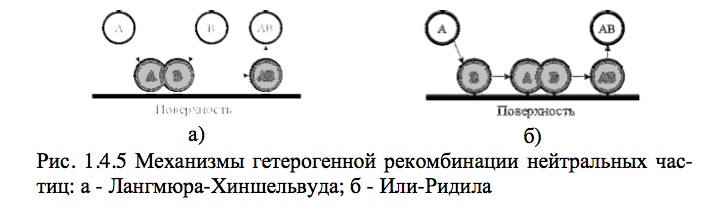
В разрядах низкого давления доминирующую роль играет гете-рогенная рекомбинация, протекающая на стенках разрядной камеры. В общем случае гетерогенная рекомбинация может протекать по двум механизмам. Первый из них, механизм Лангмюра-Хиншельвуда, предполагает взаимодействие между двумя адсорбированными частицами (рис. 1.4.5,а) и может быть представлен следующим образом:

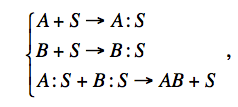где символ S отвечает поверхности, а A : S и B : S - адсорбированные состояния частиц. Эквивалентное кинетическое уравнение для скорости процесса может быть записано как R k_Rn_An_B , то есть реакция имеет второй кинетический порядок по концентрации частиц в газовой фазе. Наиболее часто реализуемым в условиях ННГП является второй механизм - механизм Или-Ридила, - когда адсорбированный атом взаимодействует непосредственно с частицей, приходящей на поверхность из газовой фазы:

Уравнение скорости процесса для частиц сорта A, например, может быть записано как R k_R n_B:S n_A , при этом n_B:S n_sθ_B где n_s - поверхностная плотность центров рекомбинации, определяемая типом и состоянием поверхности, а θ_В - доля центров рекомбинации, заполненных адсорбированными частицами сорта B . В предположении о «насыщенной» поверхности (все центры рекомбинации заняты адсорбированными частицами, θ_В = 1) скорость рекомбинации описывается кинетическим уравнением первого порядка R k_R n_A .