Задача о назначениях

Пусть имеется n видов станков различных типов, которые требуется распределить между n видами работ. Известен ожидаемый эффект су от ис­пользования i-го вида оборудования наj-м виде работ, измеряемый, напри­мер, количеством обрабатываемых деталей. Задача состоит в таком назначе­нии станков на виды работ (по одному станку на каждый вид работы), чтобы суммарный эффект от использования всех станков был максимален (напри­мер, число обрабатываемых деталей).

Математическая модель. Введем переменные ху, определяемые фор­мулой

Г 1, если -ijй станок предназначен для-го вида работ; х.. = <

10 — в противном случае.

14

Необходимо найти такие значения переменных xij, которые будут мак-

п п

симизировать суммарный эффект, т. е. max ^ c ijxij при условиях:

i=i j=\

1) ∑x_: = 1 (для каждого вида работы предназначен только один станок);

2) ∑ x_ij = 1 (каждый станок предназначается только на одну работу).

К рассмотренным выше основным типам задач линейного программи­рования можно свести многие их разновидности.

Постановка задачи и основные определения злп

В общем виде задачу линейного программирования (ЗЛП) можно запи­сать следующим образом: найти

max / (jcj, .. .,х_п ) = max c^tjc = max ^ CjXj = max^JCj + c₂x₂ н 1- c_nx_n)

или

п

j = min()c1x1 + c₂x₂

при ограничениях Ax = ∑ aijxj где n 1 ≤n.

b_t i = \,m, x>0 j =

Здесь

x^т= (x1, x₂ , … , x_n) — n-мерный вектор переменных (план задачи),

cт= (c1, c₂ ,…, c_n) — n-мерный вектор коэффициентов целевой функции,

А = {a_{ij }} \ — матрица коэффициентов левой части системы

ограничений,

15

b^т= (b1,b₂ ,…, b_m) — вектор коэффициентов правой части системы огра­ничений.

Формы записи общей злп

Различают две основные формы записи ЗЛП: стандартная и канониче­ская. Будем рассматривать в качестве стандартной ЗЛП

m ax ∑ CjXj , при ограничениях ∑ aijxj ≤b_i, i = 1,m, хj ≥ 0, j= 1, n,

каноническая ЗЛП записывается так:

п п

max∑ cjxj , при ограничениях ∑a i_jxj ⁼bi,i = 1,m, хj ≥ 0, j = 1,n.

От задачи на максимум можно всегда осуществить переход к задаче на минимум и наоборот. Если целевая функция сводится к нахождению

minf= c1x1 + c2x2 + …+ c_nx_n, то можно перейти к задаче нахождения

maxf1 = -f= -c1x1- c₂x₂ - _–… - c_nx_n, поскольку

minf= -max (-f).

Переход от общей ЗЛП к стандартной осуществляется следующим об­разом.

1. Ограничение-неравенство ЗЛП, имеющее вид «≥», можно преобразо­ вать к неравенству вида «≤», умножив обе части исходного неравенст­ ва на «-1».

1. Ограничение-равенство

16

a_i1x1 + a_i2x₂ +…+ a_inx_n=bi можно записать в виде двух неравенств:

^па^Х2

3. Если переменная хk не удовлетворяет условию неотрицательности, т. е.:

а) хk≤ 0, то заменим ее на переменную yk≥ 0 такую, что хk= —y ^k_;

б) хk — не определена, то заменим ее на разность двух переменных

Щ > О и vk ≥ 0, приняв xk = Щ - vk .

Переход от стандартной ЗЛП к канонической осуществляется путем преобразования ограничений — неравенства вида «≤» к строгим равенствам добавлением к левой части неравенства дополнительной переменной, т. е.

ai1x1 + a_i2x₂ +... + a_inx_n ≤ b_i преобразуется в неравенство

a_i1x₁ + a_i2x₂ +... + a_inx_n + x_n+1 = b_{ (x_n+l ≥ 0).

Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений-неравенств в ограничения-равенства равно числу преобразуемых неравенств.

Вводимые дополнительные переменные имеют вполне определенный экономический смысл. Так, если в ограничениях исходной стандартной ЗЛП отражается расход и наличие производственных ресурсов, то числовое зна­чение дополнительной переменной в плане задачи, записанной в канониче­ской форме, равно объему используемого соответствующего ресурса. Обрат­ный переход от канонической к стандартной форме записи ЗЛП проводится по правилам перехода от общей ЗЛП к стандартной.

Данные формы записи ЗЛП и правила перехода от одной формы к дру­гой имеют практическое значение при решении ЗЛП различными методами, рассматриваемыми ниже. Далее введем основные определения, связанные с решением ЗЛП.

Всякое неотрицательное решение системы ограничений задачи линей­ного программирования называется планом.

17

Будем называть любой план задачи линейного программирования до­пустимым, если он удовлетворяет условиям ограничений задачи.

Допустимый план будем называть опорным, если в нем отличны от нуля не более m+n-1 компонент, а остальные —равны нулю.

Если в опорном плане число отличных от нуля компонент равно в точ­ности n+m-1, то план является невырожденным, иначе — вырожденным.

Допустимый план, при котором целевая функция задачи линейного программирования принимает свое минимальное значение, называется оп­тимальным планом.

18

Лекция 1.1.3. Графический метод нахождения решения линейных

моделей. Геометрическая интерпретация решения.

Метод прямого перебора

Графический метод решения ЗЛП

Когда ЗЛП содержит всего две переменные, нетрудно получить ее гео­метрическую интерпретацию и решить задачу графически. Случай двух пе­ременных не имеет особого практического значения, однако его рассмотре­ние делает ясными отдельные свойства задачи ЛП, а также геометрический смысл методов ее решения.

Найдем решение задачи, состоящей в определении максимального зна­чения функции

f= c1x1 + c2x2 →max (1.1)

при условиях

a i1x 1+ ai₂x₂≤bi, i = 1,m, {i.2)

x ≥ 0 / = 1,2^. Г1 3⁴»

Каждое из неравенств системы ограничений (1.2) геометрически опре­деляет полуплоскость, граница которой задается прямой ац х\ + a_i2 x₂ = b_i (i = 1,m). Чтобы найти, какую именно из двух полуплоскостей определяет

д анное неравенство а_пх_х + a_i2x₂ ≤ b_i (i = 1,m), достаточно подставить в него координаты любой точки, не лежащей на граничной прямой. Если при этом неравенство будет выполняться, то искомая полуплоскость та, в которой ле­жит взятая точка, а если нет, то противоположная ей.

В том случае, если система неравенств (1.2), (1.3) совместна, область ее решений есть множество точек, принадлежащих всем указанным полуплос­костям. Так как множество точек пересечения данных полуплоскостей — выпуклое, то областью допустимых решений задачи (1.1)—(1.3) является выпуклое множество, которое называется многоугольником решений.

ЗЛП состоит в нахождении такой точки многоугольника решений, где целевая функция принимает максимальное решение. Эта точка существует

19

тогда, когда многоугольник решений не пуст и на нем целевая функция огра­ничена сверху (для задачи на максимум). Тогда необходимо построить ли­нию уровня c1x1 + c₂x₂ = h (где h — произвольная константа), затем эта ли­ния передвигается в направлении вектора с^т ={с\, c2).

Вектор с^Т =(cj; c2) называется градиентом целевой функции или век­тором роста функции, и показывает направление ее роста (соответствен­но, вектор с^Т = (- Си - c2) показывает направление уменьшения значений це­левой функции). Перемещение осуществляется до тех пор, пока линия не пройдет через последнюю ее общую точку с многоугольником решений. Ко­ординаты указанной точки и определяют оптимальный план данной задачи.

При нахождении решения задачи ЛП графически могут встретиться случаи, когда:

а) целевая функция принимает максимальное значение в единственной точке допустимого множества (единственное решение);

б) целевая функция принимает максимальное значение в любой точке от­ резка (если линия уровня совпадает с ограничением, тогда имеем слу­ чай бесконечного множества решений);

в) целевая функция может быть не ограничена на множестве допустимых решений (т. е.fmax = +∞ — это также случай бесконечного множества решений);

г) решения задачи (1.1)—(1.3) не существует, поскольку система ограни­ чений этой задачи несовместна.

Нахождение минимального значения линейной функции при данной системе ограничений отличается от нахождения ее максимального значения при тех же ограничениях лишь тем, что линия уровня c1 x1 +c2 x2 = h пере-

-*-Т

двигается не в направлении вектора ^с =(cl; c2), а в противоположном.

Алгоритм графического метода решения ЗЛП включает в себя, таким образом, следующие этапы.

1. Построение прямых, уравнения которых получаются путем замены в ограничениях (1.2), (1.3) знаков на равенства.

1. Нахождение полуплоскостей, определяемых каждым ограничением за­ дачи.

20

3. Определение многоугольника решений.

3. Построение вектора с^т ={с\, c₂).

3. Построение прямой c1x1 +c2x2 = h.

3. Перемещение прямой c1 x1 +c₂x₂ = h в направлении роста вектора с , в результате этого либо определяется точка (точки), в которой целевая функция принимает максимальное значение, либо устанавливается не­ ограниченность функции сверху на множестве допустимых решений.

3. Определение координат точки максимума функции и значения в этой

точке.

Пример. Для производства двух видов изделий А и В предприятие ис­пользует сырье двух видов. Нормы расхода сырья каждого вида на изготов­ление единицы продукции данного вида, прибыль от реализации одного изде­лия каждого вида и общее количество сырья каждого вида приведены в табл. 1.1.

Таблица 1.1

Вид сырья	Нормы расхода сырья на одно изделие, кг		Общее количе­ство сырья, кг
	А	В
I II	1 1	1 4	30 84
Прибыль от реализации одного изделия, руб.	3	4	—

Решение. Построим экономико-математическую модель задачи. Пусть jci — количество изделий типа А, х₂ — количество изделий типа В. Тогда прибыль от реализации можно записать как 3 х1 + 4 х₂ —→ max. Ограничения по использованию сырья будут выглядеть следующим образом:

21

> 0, х2 ≥ 0, так как объем производства не может быть отрицательным. Строим график (рис. 1.1).

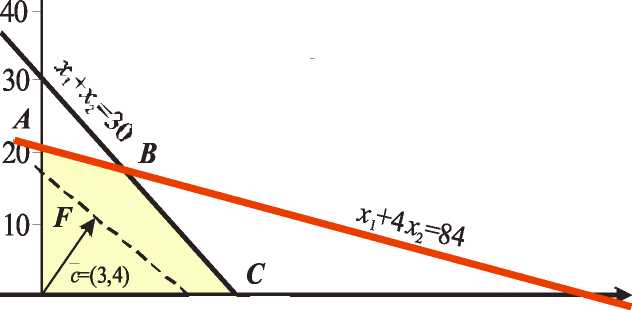О

10 20

^0^

405060 70 80

Рис. 1.1. Графическое решение к примеру

1. Прямая х1 + х2 = 30 проходит через точки (0; 30) и (30; 0). Прямая jci + 4 х₂ = 84 проходит через точки (0; 21) и (84; 0).

1. Полуплоскости, определяемые неравенствами задачи, находят путем подстановки произвольной точки плоскости, например точки (0; 0) в неравенства. В данной задаче точка (0; 0) удовлетворяет обоим нера­ венствам, следовательно, полуплоскости лежат в той стороне от гра­ ничных прямых, где находится точка (0; 0). Ограничения х1 ≥ 0, х₂ ≥ 0 определяют первый координатный угол в декартовой системе коорди­ нат.

1. Многоугольником допустимых решений является четырехугольник О АВС. Строим вектор с^т=(3; 4) или совпадающий с ним по направле­ нию с^т=(30;40).

1. Строим прямую 3 х1 + 4х₂= 12, которая проходит через точки (0; 3) и (4; 0).

1. Передвигаем прямую F в направлении вектора с. Последней общей точкой с многоугольником решений является точка В, значит, это и есть точка максимума.

22

6. Определяем координаты точки В. Для этого необходимо решить систе­му из двух уравнений

^х\ ¹2+ = 30, 484.

Решением системы является точка х1* =12, х₂ = 18. Следовательно, если предприятие изготовит 12 изделий типа А и 18 изделий типа В, то получит прибыль, равную 3·12 + 4·18 = 108 (руб.).