3. Способ определения наличия установившегося режима в некоторых процессах
Ряд процессов с некоторым приближением может быть разделен на три периода. Так, например, процесс износа некоторых деталей машин может быть разделен на следующие три периода:
первый период — период приработки, когда интенсивность отказов изделия несколько повышена из-за приработочных отказов (рис. 3);
второй период — период установившегося режима, когда интенсивность отказов, а следовательно вероятности отказов, принимают постоянные значения. В этом случае марковская цепь представляет собой однородную цепь;
третий период - период интенсивного износа изделия, наступающего вследствие быстрого старения элементов изделия.
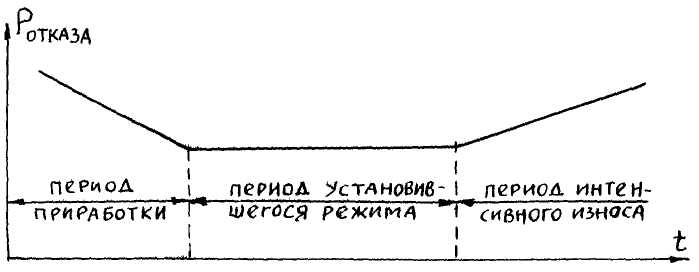
Рис. 13. Изменение интенсивности отказов изделия в зависимости от времени его эксплуатации
Однако не все процессы имеют установившийся режим. Проверка наличия установившегося режима производится в следующем порядке:
1. Если в матрице перехода системы из состояния в состояние Pij все элементы больше 0, то процесс, отвечающий исследуемой системе, имеет установившийся режим.
2. Если в матрице вероятности перехода Pij имеется хотя бы один 0, тогда для определения наличия установившегося режима необходимо:
а) составить характеристическое уравнение;
б) вычислить определитель характеристического уравнения и найти его корни, и если при этом один корень характеристического уравнения равен единице, а остальные меньше единицы, то установившийся режим существует. В противном случае установившегося режима нет.
Рассмотрим эти утверждения на примере.
Пример. Задана матрица вероятностей перехода системы в виде:
.
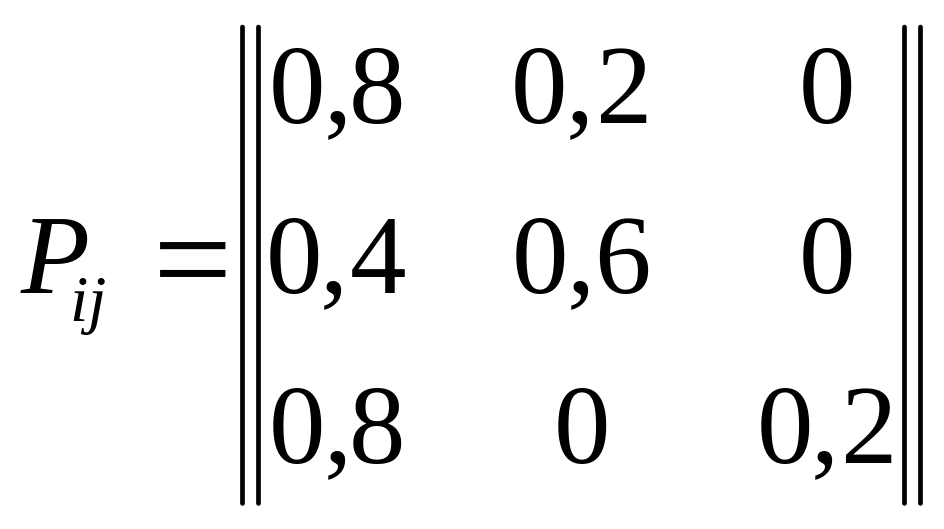Требуется определить наличие установившегося режима.
Решение.
1. Составляем характеристическое уравнение
.
2. Вычисляем определитель характеристического уравнения, например, путем приписки строк справа и приравниваем его нулю
,
Det
= (0,8 -
)
(0,6 -
)
(0,2 -
)
- (0,2 -
)
0,4
0,2
= 0,
При этом корни характеристического уравнения составляют:
1 = 0,2; 2 = 1; 3 = 0,3.
Таким образом для заданных условий установившийся режим существует.
4. Определение матрицы вероятностей состояний системы для установившегося режима
После установления наличия установившегося режима вычисляют матрицу вероятностей состояний системы.
Для установившегося режима справедливо следующее выражение
,
uде К – число шагов (к=1,2,3,4…n).
В соответствии с рекуррентной формулой
или
или
.
Для рассматриваемого выше примера получаем:
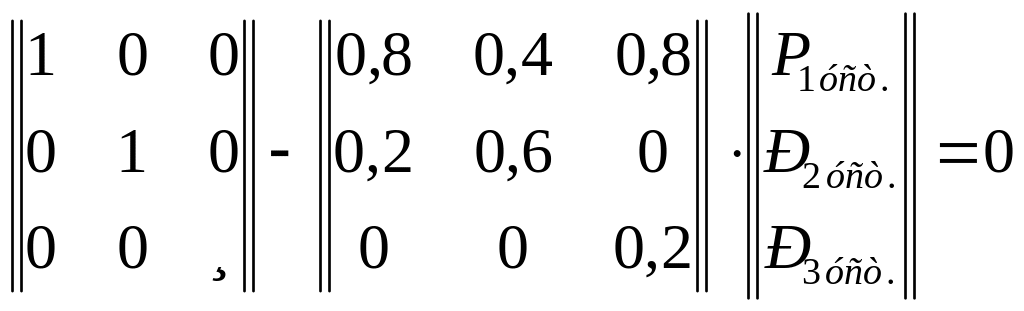или
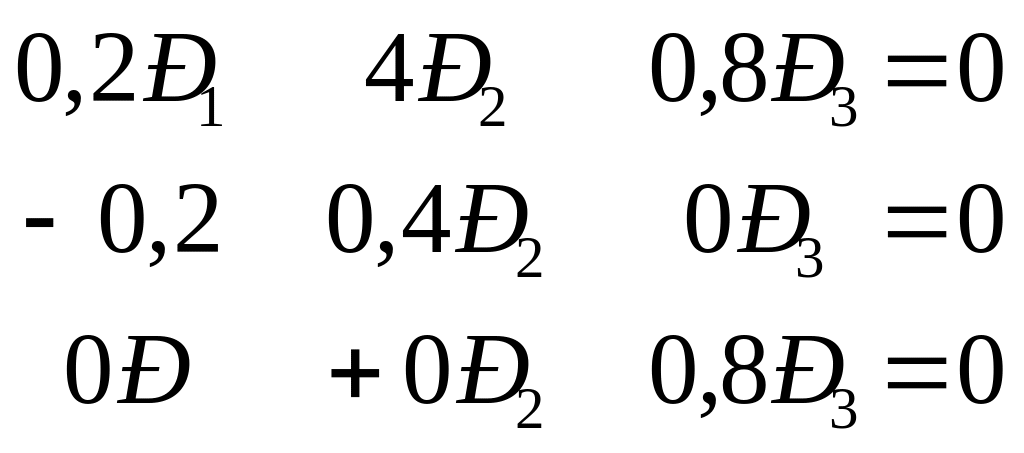(1)
Кроме того:
Р1 + Р2 + Р3 = 1 (2)
Решая совместно уравнения (1) и (2) получаем матрицу вероятностей состояний системы для установившегося режима:
.
В теории марковских случайных процессов распределение вероятностей для установившегося режима называют инвариантным, или стационарным распределением.
Рассмотренные основные положения марковского случайного процесса, в частности порядок определения вероятностей состояний системы для установившегося режима, позволяют производить сравнительную оценку различных способов организации исследуемого технического или экономического процесса, и на основании этого выбрать из них оптимальный способ.