2.1. Сфера применимости и предпосылки построения линейных моделей

Широкое распространение в экономике линейных моделей (или, как еще говорят, линейного программирования) связано, во-первых, с тем, что многие экономические операции с достаточной точностью могут быть описаны линейными моделями; во-вторых, за небольшим исключением только для этих моделей разработаны эффективные методы численного решения при приемлемой для практики размерности задачи.

Примерами использования линейных моделей могут служить модели комплексного использования сырья, транспортная, размещения производства, перспективного планирования, развития экономического комплекса, различных ситуаций оперативного управления и т. д. Широко применяются такие модели и в связи с необходимостью анализа ситуаций, возникающих в экономике из-за большого числа возможных вариантов функционирования конкретного объекта при использовании различных видов сырья, материалов, технологий и других факторов.

Использование линейных моделей опирается на возможность рассмотрения плана (вектора управляемых переменных) в расчлененной форме, составленного из элементарных процессов, которые могут протекать с различной краткостью (интенсивностью). Также предполагается, что приращение критерия оптимальности и невязок условий задачи пропорциональны изменениям соответствующих управляемых переменных. Что, в частности, означает: увеличение выпуска продукции в некоторое число раз требует увеличения потребления объектом всех других продуктов в то же самое число раз.

Для многих задач планирования и управления такие допущения выглядят вполне приемлемыми и позволяют получать хорошие результаты.

Вместе с тем необходимо четко представлять границы линейности показателей, включаемых в модель операции. Известно, что существует так называемая условно постоянная часть расходов, не зависящая от количества выпускаемой продукции в определённом диапазоне изменения объемов. При интенсификации процессов могут меняться нормы расходов на единицу выпускаемой продукции тех или иных ингредиентов. Эти и ряд других моментов приводят к нарушению линейности объектов, выделяя тем не менее достаточно обширную сферу применимости линейных моделей в операционном анализе экономических ситуаций.

Лекция 2.2. Математические модели исследуемых процессов основанные на уравнениях регрессии, используемых при определении оптимальных решений.

При решении задач исследования операций могут применяться различные по своему характеру и степени абстракции математические модели.

В этой лекции рассматривается порядок определения оптимальных решений для случая, когда математические модели исследуемых процессов или явлений заданы в виде уравнений регрессии.

2.2.1. Виды математических моделей, описываемых уравнениями регрессии

При использовании статистических методов математические модели чаще всего представляются в виде следующих зависимостей, называемых уравнениями регрессии. Многофакторная линейная модель

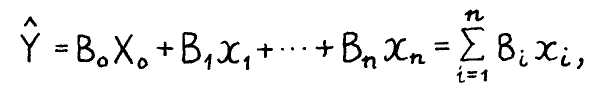
где — функция отклика, параметр оптимизации (расчетное значение, получаемое на основе обработки опытных данных);

X_i _ факторы, оказывающие влияние на функцию отклика;

B_i — коэффициенты при факторах. Многофакторная квадратичная модель

Поскольку в реальном процессе всегда существуют неуправляемые и неконтролируемые переменные, постольку изменение величины носит случайный характер. Это значит, что получаемые на основе обработки опытных данных выборочные коэффициенты В₁, B₂.,.. ,B_n, являются лишь оценками действительных коэффициентов уравнений регрессии.

При вычислении выборочных коэффициентов регрессии, как правило, применяется метод наименьших квадратов.