Тема 2. Методологии моделирования процессов. Линейные модели в операционном анализе организационных систем.

Лекция 2.1. Сущность методологии моделирования

Использование математических методов для анализа экономических ситуаций предполагает предварительное описание изучаемой экономической системы математическими соотношениями, другими словами, создание математической модели этой системы.

Большинство экономических систем представляются сложными системами. Они характеризуются большим числом параметров, меняющихся во времени. Сложность анализа экономических систем в том, что существенной их составляющей являются люди, принимающие решения на основе разнообразной информации с учетом различных целей. Кроме того, экономическая система непрерывно подвергается множеству случайных, трудно прогнозируемых возмущений как извне (изменение количества и номенклатуры поставок, изменение спроса и т. д.), так и изнутри (появление новых технологий, поломка оборудования, несовпадение реальных сроков с планируемыми и т. д.).

В то же время экономико-математическая модель должна быть достаточно простой и обозримой, чтобы ее можно было записать, получить необходимые для записи данные, а если модель расчетная, то поместить полученную информацию в память ЭВМ. Математическая модель всегда «беднее» реальной моделируемой системы, всегда описывает систему лишь приблизительно, выделяя одни свойства системы и пренебрегая другими. Выбор важнейших свойств для учета в модели представляет собой искусство моделирования и определяется умением исследователя операций выделить (исходя из целей анализа) главное из большого количества факторов, цифр и соображений, затрудняющих решение задачи. Исследователю операций не говорят, какие данные необходимо собрать для решения задачи, а также где и как их найти. Часто сбор необходимых данных требует изучения таких факторов, которые на первый взгляд не имеют отношения к предложенной задаче.

Модель создается тогда, когда, по убеждению исследователя, существует некая аналогия между реальной системой и его представлениями. При отсутствии достаточной информации об исследуемых объектах или процессах их изучение начинается с построения простейших моделей. Модели в исследовании операций служат для объединения опытных факторов и нахождения взаимосвязи между параметрами.

Конечная цель разработки математической модели — прогноз результатов проведения операции и выработка рекомендаций по возможным воздействиям на ход ее проведения. При этом необходим четкий анализ сферы и границ применимости полученных результатов. Обычно модели создаются на основе теоретических положений или гипотез, объясняющих полученные в результате наблюдений данные. Модели не следует считать неизменными, их нужно трактовать как инструмент анализа и понимания экономического процесса или системы. Для изучения одного и того же объекта или процесса может быть предложено несколько моделей, соответствующих целям анализа. При создании модели, обосновывающей возможное принятие решения о развитии конкретной ситуации, важное значение имеет количество выделяе­мого времени. Если требуется срочно выдать результаты, то создание сложной модели нецелесообразно. Во многих случаях модель нужна лишь для грубой оценки влияния отдельных факторов на результат. Подробное теоретическое исследование здесь также нецелесообразно.

Модель должна по возможности обладать «внутренней гибкостью», т. е. допускать возможность использования непредусмотренной новой информации. Сбор и обработка исходной информации являются важной частью исследования операции. К сожалению, при решении большинства практических задач не удается собрать нужный объем данных, необходимый для создания достаточно подробной модели процесса или объекта, охватывающей все аспекты задачи.

При рассмотрении экономико-математической модели оперируют следующими основными понятиями: «критерий оптимальности», «целевая функция», «система ограничений», «уравнения связи», «решение модели».

Целевую функцию нельзя отождествлять с критерием оптимальности: различные критерии могут описываться одной и той же целевой функцией.

Целевая функция математически связывает факторы модели (прежде всего переменные, «управляющие»).

Система ограничений определяет границы, сужающие область осуществляемых, приемлемых или допустимых решений, и фиксирует основные свойства моделируемого объекта или процесса. Ограничения устанавливают границы изменения параметров — характеристик объекта.

Уравнения (соотношения) связи являются математической формализацией системы ограничений.

Под критерием оптимальности обычно понимают экономический показатель, содержащий в формализованном виде конкретную цель управления объектом или процессом и выражаемый математически при помощи целевой функции через факторы модели.

Таким образом, критерий оптимальности выражает содержательное, смысловое значение целевой функции. Иногда в качестве критерия опти­мальности может выступать одна из интересующих исследователя конечных характеристик объекта.

Решением экономико-математической модели обычно называют набор переменных, удовлетворяющий уравнениям связи. Решения, имеющие экономический смысл, называются допустимыми. Модели, имеющие более одного решения, называются вариантными. Среди допустимых решений вариантной модели находится решение, при котором целевая функция в зависимости от смысла модели имеет наибольшее или наименьшее значение. Такое решение (как и соответствующее значение целевой функции) называется оптимальным.

Применение экономико-математической модели, в особенности оптимизационной, при исследовании операций предполагает не только построение модели, но и получение решения при помощи подходящего метода. Поэтому иногда под моделированием (в более узком смысле) понимают этап нахождения решения. Выбор метода решения зависит от математической формы модели.

С точки зрения целей операционного анализа математические модели операций в экономике делятся на оптимизационные (нормативные) и дескриптивные (описательные или экономико-математические модели прямого счета). Важнейший признак дескриптивной модели — отсутствие критерия оптимальности. Решение модели сводится к вычислению выходных характеристик объекта по заданным начальным условиям. Примерами дескриптивных моделей могут быть модели расчета объемов производства по видам продукции, увязки планов производства с ресурсами (балансовые модели), а также модели оперативного учета, получения форм отчетности, анализа влияния факторов, прогнозирования показателей и ряд других. Модели этого типа позволяют решать задачи анализа, предлагающие ответ на вопрос: «Что будет, если…?».

Когда перед исследованием операции стоят задачи синтеза, требующие ответа на вопрос: «При каких значениях управляющих параметров будет достигнуто…?», необходима оптимизационная модель, характерной чертой которой является наличие одной (однокритериальная модель) или нескольких (многокритериальная) целевых функций. В общем виде однокритериальная модель может быть описана следующими соотношениями:

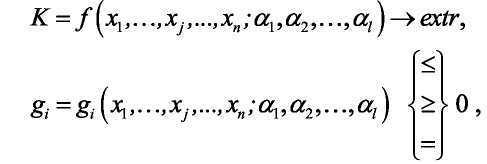
где K — критерий оптимальности;

/— целевая функция — формализованное описание критерия оптимальности;

g i — уравнения связи, i = 1,m;

xj—управляемые переменные, j = 1,n;

α_k — неуправляемые факторы модели, k = 1,l.

Решение модели заключается в нахождении множества значений управляемых переменных обращающих в max или min целевую функцию и удовлетворяющих уравнениям связи.

Учет специфики конкретных операций определяет разнообразные оптимизационные экономико-математические модели. Однако для некоторых часто повторяющихся ситуаций разработаны общие методы построения моделей. Исторически и содержательно наибольший интерес представляют линейные модели, т. е. те модели, в которых целевая функция и уравнения связи являются линейными функциями.