СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Курс: Исследование операций и методы принятия решений

(Конспект лекционных материалов)

Для студентов специальности «Организация и безопасность движения» (железнодорожный транспорт) 2404

Красноярск 2010 г.

Тема. Введение

исследования операций как научная дисциплина. История появления.

Термин "исследование операций" впервые использовал, по-видимому, А. Рауф, руководитель одного из подразделений технической службы ВВС Великобритании, применительно к разработке эффективной тактики ведения военных действий (операций). Это было в 1939 г., а в 1941 г. в английской армии уже действовали многочисленные отделы исследования операций (подробней историю возникновения и развития исследование операций.

Подходы и математические модели, развитые в рамках исследования операций, оказались применимыми не только в военном деле, но и в технике, промышленности, экономике, управлении. Поэтому теперь термин "операция" трактуют очень широко: как любое целенаправленное действие (мероприятие, совокупность мероприятий).

Целенаправленность возможна, только если операция управляема, ее исход зависит от управляемых параметров. Совокупность значений управляемых параметров — это решение (управление, план), и его, естественно, определяет лицо, принимающее решения, — ЛПР (этот термин может относиться и к группе, например к Совету директоров). ЛПР отвечает за результат операции.

Исследование операций изучает целенаправленные действия, и главным инструментом исследования конкретной операции является ее математическая модель . В литературе можно найти множество формулировок предмета исследования операций: разработка систематического и рационального подхода к решению задач управления системами; научный подход к решению задач организационного управления; применение математических методов для обоснования оптимальных решений во всех областях целенаправленной человеческой деятельности; изучение и объяснение явлений, связанных с функциональными системами. А. Кофман характеризует исследование операций как науку о подготовке решений, а Т. Саати — как "количественное выражение здравого смысла" и "искусство давать плохие ответы на те вопросы, на которые другими способами даются еще худшие ответы..

Научный (количественный, математический) анализ ситуации, применение методов исследования операций к реальной операции (операционное исследование) обычно выходят за рамки обязанностей и/или возможностей ЛПР. Поэтому ЛПР поручает (заказывает) операционное исследование специалисту, исследователю операций (операционисту). Операционист не принимает решений и не отвечает за их последствия, он дает рекомендации и отвечает за их обоснованность. ЛПР принимает во внимание эти рекомендации, но не всегда им следует: опыт и интуиция (или авантюризм и самонадеянность) могут подсказать ему другое решение. Исследователь, таким образом, только готовит информацию для принятия решений.

Итак, предмет исследования операций — подготовка информации для принятия целесообразных решений, а метод — построение и анализ математической модели операции.

Тема 1. Основные положения исследования операций как науки

1.1. Общие сведения

Как уже отмечалось выше, исследование операций — это методология или комплекс научных методов, с помощью которых могут решаться самые сложные современные задачи техники, экономики и науки. Исследование операций — это часть кибернетики, которая занимается вопросами организации управления.

Операционное исследование — творческий процесс, который невозможно (и не следует) унифицировать. Однако структуризация этого процесса возможна и полезна.

Операцией — называют любое мероприятие, или систему действий, объединенных единым замыслом и направленным к достижению определенной цели.

Типовыми задачами исследования операций, например, являются:

• задача оптимального использования парка автомобилей или парка дорожно-строительных машин данного района или города;

• задача оптимальной организации диагностики, технического обслуживания и ремонта автомобилей и дорожно-строительных машин;

• задача оптимального распределения подвижного состава по различным маршрутам и различным объектам с целью выполнения заданного плана работ;

• задача оптимальной организации систем массового обслуживания, например, выбора оптимального количества ремонтных постов и числа ремонтных бригад на станции технического обслуживания автомобилей;

• задача оптимального проектирования и строительства новых дорог, мостов, аэропортов и др. сооружений и т.п.

Эффективность .операции — это степень ее приспособленности и выполнения поставленных перед ней задач, т.е. степень соответствия своему назначению.

Критерием эффективности операций называется численный параметр или показатель, с помощью которого оценивается эффективность операции. Выбор критерия операции зависит от характера и цели операции. В качестве критерия эффективности может применяться вероятность какого—либо события Р(А) или среднее значение (математическое ожидание) случайной величины М (х).

Приведем несколько примеров критериев эффективности операций. Например, при оценке технического уровня машин в качестве критериев мо­гут служить: производительность, надежность, энергоемкость, ремонтопригодность, технологичность, показатель технической эстетики и др.

При оценке качества товаров массового потребления, например, одежды, показателями эффективности могут служить: соответствие моде, прочность, соответствие изделия форме человека и т.п.

2. Этапы операционного исследования

Исследование любой операции состоит из следующих этапов:

• описание ситуации и постановка задачи с точки зрения заказчика;

• выбор математической модели;

• составление алгоритма для избранной математической модели;

• проверка математической модели на адекватность;

• реализация решения на практике.

Рассмотрим последовательно каждый из этапов.

Сущность описание и постановки задачи

Чаще всего заказчик (ЛПР) не очень хорошо знаком с методикой и возможностями исследования операций, а исполнители (операционисты) не обладают достаточными знаниями в предметной области, к которой относится операция. Для выявления проблемы и описания операции необходимо сотрудничество исполнителей и представителей заказчика. Операционист должен подробно и непредвзято изучить объект: систему, в рамках которой выполняется операция. Утверждения и гипотезы ЛПР и его представителей следует внимательно анализировать, выявлять скрытые (возможно, неосознаваемые) мотивы и проблемы.

В ходе обследования объекта, как правило, модифицируются и уточняются цели операции и задачи операционного исследования. Заказчик и исполнитель должны добиться единого понимания содержания и целей операции. Главные характеристики операции — целесообразность и управляемость, поэтому в вербальное (словесное, содержательное) описание операции необходимо включить формулировку ее целей и перечень управляемых параметров. Структура описания операции схематически показана на рис. 1.

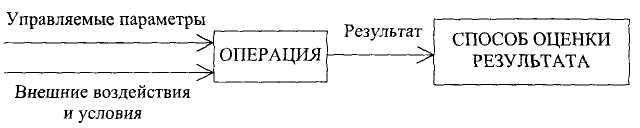
Рис. 1. Принципиальная схема описания операции

На первом этапе операционист должен дать ответы на следующие вопросы.

Какие неуправляемые параметры (воздействия внешней среды) существенно влияют на операцию, какие значения могут принимать эти параметры?

Какая информация о состоянии внешней среды будет доступна в момент принятия решения?

Какие выходные параметры описывают результат операции?

Как связаны между собой управляемые, неуправляемые и выходные параметры?

Как оценить степени достижения целей операции при данных значениях неуправляемых и выходных параметров?

Формулировка последнего вопроса требует комментариев. Результат операции зависит, конечно, от значений управляемых и неуправляемых параметров. Но этот результат может быть хорош или, напротив, совершенно неприемлем в зависимости от состояния внешней среды. Оценка результата операции зависит, следовательно, не только от собственно результирующих параметров, но и от состояния внешней среды.

Возможные исходы операции оцениваются до принятия решения, которое, собственно, выбирается на основе этих оценок. Поэтому определение способа оценки результата является серьезной проблемой, если в момент принятия решения невозможно предсказать те значения существенных характеристик внешней среды, при которых будет осуществляться операция. Понятно, что неопределенность предсказания результата операции (при фиксированном плане) не меньше, чем неопределенность воздействий внешней среды на систему (см. раздел 1.3). Предположим, например, что некоторая характеристика внешней среды известна только как случайная величина. Тогда и результат операции является для нас случайной величиной, числовые характеристики которой (скажем, математическое ожидание и дисперсию) можно использовать для построения оценки результата.

Информация, собранная на 1 этапе, позволяет сформировать правдоподобные предположения о существенных свойствах операции и объекта в целом.

Постановка задачи — это важный этап операционного исследования. Первоначально задачу формируют словесно с точки зрения заказчика. На этом этапе уясняются условия и ограничения, которые необходимо учитывать при решении задачи, а также производится качественный анализ исследуемого явления или процесса. В некоторых случаях для уяснения задачи могут производиться статистические наблюдения, т.е. сбор информации о процессе, подлежащем операционному исследованию. Собирается информация, характеризующая работу системы за прошлые периоды и в настоящее время. Информация об исследуемой системе может поступать в виде количественных показателей, т.е. в виде цифр, сигналов, сводок, требований и т. д. На этапе постановки задачи выясняется также вопрос о разрешимости поставленной задачи, т.е. производится исследование принципиальной возможности решения задачи.

Сущность выбора математической модели

После уяснения задачи и выяснения вопроса о ее разрешимости приступают к выбору вида математической модели, с помощью которой предполагается описывать изучаемое явление.

Сложность и многообразие процессов функционирования реальных систем не позволяет строить для них абсолютно адекватные математические модели.

Поэтому при составлении математических моделей отбрасывают все второстепенные факторы и оставляют лишь главные, определяющие факторы. Это значит, что математическая модель— это аналог реального явления, охватывающего лишь его основные свойства.

Математические модели являются основой прогнозирования, и, следовательно, являются основой планирования и оптимального управления исследуемым процессом.

В зависимости от условий и характера решаемых задач могут применяться различные виды математических моделей и многочисленные методы и приемы моделирования. Обычно различают физическое и математическое моделирование. На рис. 1 дан краткий спектр математических моделей, которые могут применяться при решении задач исследования операций.

В самом общем виде математическая модель представляет собой зависимость критерия (или критериев) эффективности операции от внешних неуправляемых факторов Y , от внутренней структуры системы Z и от принятого решения X по управлению исследуемым процессам

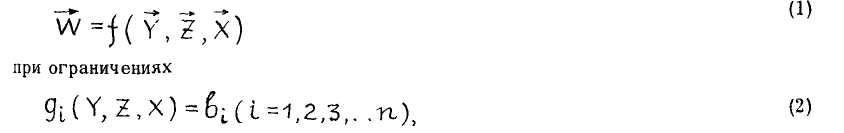
где W — критерий эффективности операции, параметр оптимизации, целевая функция и т.п.;

Y — вектор внешних неуправляемых факторов системы (природа); Z — вектор внутренних параметров структуры системы;

X — вектор управляемых факторов системы (вектор принимаемых решений);

q_i - aункция ограничений по i—той переменной;

b_i — величина ограничений по t-той переменной (так называемые дисциплинирующие условия).

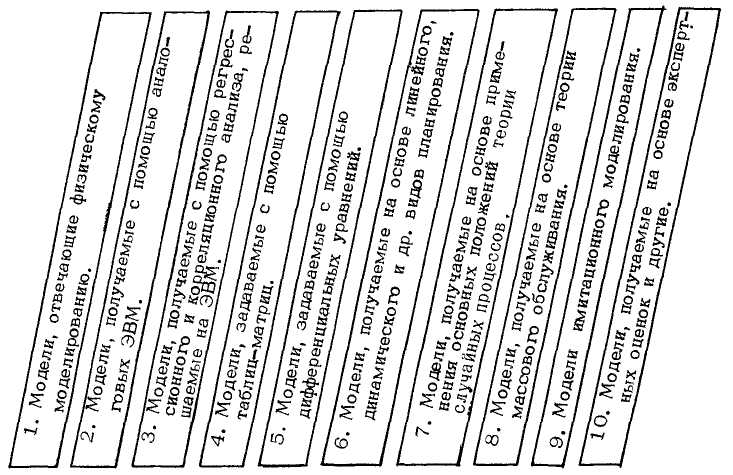
Рис. 2. Спектр математических моделей, применяемых при решении задач исследования операций

Внешние условия Y — представляют собой природу, т.е. объективную реальность, на фоне которой происходит функционирование системы. Например, время года, время суток, географическое положение объекта исследования, спрос, предложение и т.п. Постепенное изменение внешних условий называют дрейфом системы.

Неуправляемой частью структуры системы 2. , например, при решении авто — транспортными объединениями задач по транспортировке пассажиров, доставке продуктов питания, подвозе предприятиям сырья, необходимого для нормального течения производственного процесса и при решении других подобных задач, является качество автомобилей сегодняшнего дня (например, их грузоподъемность, скорость движения и т.п.), качество горюче—смазочных материалов и т д., т.е. такие факторы, которые не могут быть изменены в процессе решения задачи сегодняшнего дня.

Вместе с тем, улучшение качества продукции, и, следовательно, улучшение качества автомобилей, качества горюче - смазочных материалов и т.л. является важнейшей задачей. Это значит, некоторые неуправляемые факторы при решении задач становятся управляемыми при решении более отдаленных задач.

Управляемой частью структуры системы , являются параметры, которые в процессе решения задачи могут быть изменены по нашему желанию. Например, количество ремонтных постов на станции технического обслуживания машин, планируемые межремонтные сроки, распределения электричек по маршрутам, увеличение числа касса по продажам билетов и т. п. Управляемые параметры структуры системы параметры называют решениями или стратегиями. Иногда решения называют управлениями или альтернативами.

Графически, схема исследуемого явления или процесса, при макроподходе, как уже отмечалось выше, может быть представлена в виде черного ящика (рис. 3)

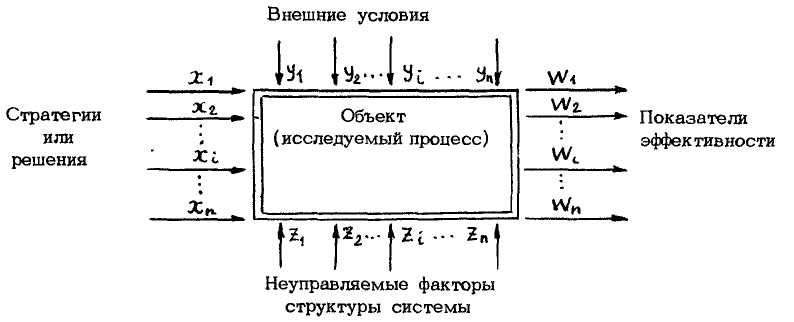
Рис. 3. Схематическое изображение объекта исследования

При исследовании сложных технических и экономических систем возникает ряд трудностей, обусловливаемых следующими обстоятельствами¹:

• некоторые параметры внешней среды не могут быть измерены в силу неполной информации. Например, при анализе функционирования транспортной системы не всегда удается с прогнозом на будущее оценить качество будущих дорог, качество обслуживания, наличие необходимых запасных частей и т.п. Неопределенность в оценке состояния внешней среды для текущего момента времени создает еще большую неопределенность в оценке ее будущего состояния. Кроме того, параметры внешней среды в процессе функционирования системы могут меняться непредсказуемым образом;

• численные параметры структуры системы оцениваются, как правило, с ошибками, обусловливающимися "шумами" измерительных средств и внешними помехами;

• часто системы обладают переменной (скользящей) структурой. Например, конструкция автомобилей претерпевает непрерывные изменения: бензиновый двигатель может быть заменен газогенераторным или электрическим» а последний в свою очередь может быть заменен турбореактивным двигателем и т.п. Подобные изменения могут также происходить в подвеске, в конструкции кузова и в других агрегатах;

• наконец, эффективность функционирования технических и экономических систем, как правило, характеризуется иерархией показателей.

Показатели высшей ступени зависят от показателей более низкой ступени, а последние в свою очередь зависят от показателей еще более низкой ступени иерархии. Все выше перечисленные особенности усложняют решение задачи по исследованию сложной системы.

При исследовании сложных систем задачи могут быть разделены на два вида:

1. задачи анализа, когда при заданных значениях Y , Z, X определяется эффективность функционирования системы, W (см. формулу 1);

2. задачи синтеза, когда при заданных Y, Z и W определяется вектор оптимальной стратегии X, или когда при заданных значениях Y, X и W определяется вектор оптимальной структуры системы

Составление алгоритма для избранной математической модели

После выбора вида математической модели и формализации исследуемого процесса заключающейся в отбрасывании всех второстепенных факторов, модель представляют в виде уравнений, графиков, схем и т.л. Указанную формализованную математическую модель называют алгоритмом процесса. Решение задачи с помощью получаемого алгоритма производится, как правило, с помощью ЭВМ. Для этого полученный алгоритм представляют в виде операторной блок—схемы. Далее, на одном из машинных языков составляется программа для решения задачи на ЭВМ.

Проверка математической модели на адекватность

Оценка математической модели на адекватность является весьма важной задачей. Эта проблема является достаточно сложной, так как она связана с многими логичес­кими, практическими и статистическими вопросами. В зависимости от условий провер­ка модели на адекватность может производиться, например, с помощью следующих способов:

• сличением полученных с помощью модели выходных данных с аналогичными данными, полученными на практике за прошлые периоды времени, если они имеются (практика—критерий истины);

• проверка адекватности статистическими методами, например, с помощью критериев Фишера, Стьюдента и т.л.

В случае несогласованности данных производится корректировка модели.

Реализация решения на практике

После составления математической модели, проверки ее на адекватность и ее корректировки приступают к решению поставленной задачи. Результаты решения докладываются заказчику. Опыт показывает, что при решении операционной задачи на основе хорошо подобранной математической модели получают значительный выигрыш в эффективности функционирования исследуемой системы.