Power gain (gp)

The power gain is defined as

There are, however, a number of ways in which we could evaluate power gain.

Consider the circuit below; note that hoe and Rc have again been shown separately.

We can define the power gain as

All these definitions are perfectly valid; which one is chosen depends upon

which aspect of the circuit's performance we wish to evaluate.

If we calculate the power gain as

then, having found GV and GI, finding the power gain is straightforward.

Note also that which offers an alternative method

of calculating the power gain:

One final word of caution! In the above discussion on power gain we have

assumed that the load is resistive. If, however, this is not the case, then due

regard must be paid to the phase relationship between voltage and current.

Let’s consider the example.

For the equivalent circuit shown

CL = 10 nF hfe = 100

RL= 1khie= 1kGo= 10 ^–4 S CC = 10 F

calculate:

(i)the mid-band current gain (IL/Ii)

(ii) the mid-band voltage gain (Vo/Vi)

2. the mid-band power gain (power in load/power input)

(iv) the lower half-power frequency

(v) the upper half-power frequency

(vi) the bandwidth

(vii) The magnitudes of the current and voltage gains and the power gain

at = 220 10³ rad s^–1.

1. Mid-band current gain

2. Mid-band voltage gain

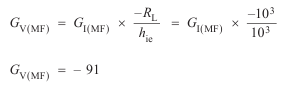
(iii)Power gain

(iv) Lower half-power frequency

f₁=₁/2z

(v)Upper half-power frequency

f₂=₂/2z

(vi)

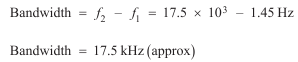
(vii) As 220 10³ rad s^–1 > 2, we must use the high frequency equations for

GI and GV.

Current gain

Voltage gain

Power gain

Again, as the power gain has been defined as where IL is

the current through a resistive load, we can write