The effects of frequency and the model

The voltage and current gains of an amplifier are frequency dependent. The

variation of gain with frequency is due to capacitive effects. The source of

such effects is twofold:

(i) coupling capacitors

(ii) internal capacitances of the amplifier.

Let us briefly examine each of these sources in turn.

1. The effects of coupling capacitors placed in the circuit

note the coupling capacitors C1 and C2.

The purpose of these capacitors is to couple, from an a.c. point of view,

the input and output of the amplifier to other stages, without upsetting the

d.c. conditions on the amplifier.

Within the designed frequency range of operation, the coupling capacitors

should behave as short circuits to signals.

Within this range the amplifier can be represented by the simple 'black

box' model as

If we are working outside the designed frequency range of the amplifier,

however, we may have to include the coupling capacitors in the model as

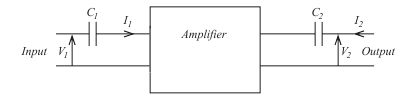
Remember, that a capacitor's reactance falls with increasing frequency. Thus, if a coupling capacitor can be regarded as a short circuit within the designed operating

range, then this assumption will be even more valid at frequencies above this

range. At frequencies below this range, however, the effects of the coupling

capacitors cannot be ignored.

(II) Internal capacitances of the device within the box

There can be many causes of 'internal' capacitance. For example, in the

case of a transistor amplifier there are the interelectrode capacitances of

the transistor itself. The diagram below shows the three interelectrode

capacitances of a transistor.

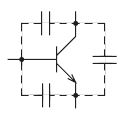
It can be possible to show that two of these capacitance effects can be represented by a single equivalent capacitor Ci. Our black box model can be amended, if required, to include this equivalent input capacitance.

Remember, that the capacitance Ci appears in parallel with the input resistance of the amplifier. If, within the normal frequency range of the amplifier the effects of

Ci can be ignored, then this will be even more true at frequencies below this

range. At higher frequencies, however, the reactance of Ci will fall and its

effects cannot be ignored. It will tend to shunt the input resistance.

Effects of a capacitive load on the amplifier

In the foregoing discussion we have identified the possible causes of reactance

which could limit the frequency performance of our electronic black box.

Imagine, now, that one black box is used to drive another, as shown below

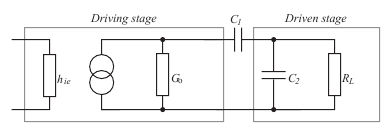
The driving stage is represented in the usual way by an input equivalent circuit,

in this case simply a resistance, and an output equivalent circuit consisting of a

current generator and the output conductance Go. This conductance is due to

the combined effects of the transistor's output conductance, hoe, in parallel with

the collector resistor Rc. The driving stage is coupled by C1 to the driven stage.

Only a modified input equivalent circuit is shown for the output circuit. It

consists of a capacitance C2 in parallel with a resistance RL.

C2 and RL represent the total loading of the second stage upon the first. To

predict the frequency behavior of the circuit, all we need do is to express

the current and voltage gains as a function of frequency. It is usually possible to identify three different frequency ranges in which an amplifier can operate. This will enable us to ignore some, or even all, of the capacitive effects within a particular range.

________________________________________________________________________________________

THE THREE FREQUENCY RANGES OF OPERATION

________________________________________________________________________________________

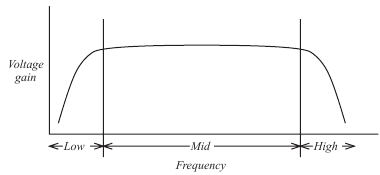
You can see the typical frequency response of an amplifier.

The graph can be seen to consist of three ranges:

(i) a low-frequency range in which the gain increases with increasing

frequency

(ii) a mid-frequency range over which the gain is relatively constant

(iii) a high frequency range over which the gain falls with increasing

frequency.

For simplicity, let's consider the mid-frequency range first.

THE MID-FREQUENCY RANGE

Over this range the coupling capacitors are assumed to be behaving themselves

and may be regarded as having negligible impedance (compared to the

resistances in the circuit). They can, therefore, be ignored in any calculation.

Conversely, the box's internal capacitances, which are low in value, will have a