Пример выполнения работы

1 Выполнить на ЭВМ. диалоговую программу, проверяю­щую знание обучаемым теоремы Виета. Обучаемому выдает­ся основное задание: написать квадратное уравнение, если его корнями являются х1= <число> и х2= <число>. Значе­ния корней — случайные числа из диапазона [—9,9]. Если ответ правильный, то можно переходить к следующему за­данию, приняв новые значения корней xl, х2. Если ответ неправильный, то предложить снова ответить на то же за­дание. Если после второй попытки ответ опять не совпал с эталоном, то предложить новые дополнительные вопросы:

1) ввести коэффициент перед х в первой степени со знаком;

2) ввести свободный член со знаком. Если оба этих ответа правильные, то признать ответ правильным, вывести его и пе­рейти к следующему заданию. Если ответ на какой-либо из этих заданий неправильный, то можно судить о причине ошибки.

Выполнение программы закончить, если подряд три ответа на вопросы были правильными с первой попытки или или общее число вопросов равно 10. В программе предусмотреть помощь обучаемому, подсчитать число основных заданий п, число правильных ответов с первой попытки n₀, общее число ответов n₁. По результатам контроля определить оценку: «5», если n₀ = n; «4», если n - n₀≤2; «3», если n - n₀≤4;

«2», если n - n₀>4 или n≥10.

Алгоритм решения может быть следующим. Организуем цикл по числу основных вопросов i от 1 до 10. Для каждого основного вопроса с помощью датчика равномерно распреде­ленных случайных чисел получим два случайных числа — y₁ и y₂ из диапазона [0, 1]. Затем вычислим два случайных числа x₁ и x₂ из диапазона [—9, 9], которые являются корнями квадратного уравнения. Обучаемому выведем сообщение: «Определите квадратное уравнение, если его корни равны xl = <число>, х2= <число> и введите ответ», где x1 = <чис­ло 1> и х2= <число 2> — значения корней х₁ и х₂.

Сформируем эталон правильного ответа. Для этого в начале программы в массив или строковую переменную W (где размещается эталонный ответ) введем следующую информацию:

Х*Х *Х =0

Так как результатом решения задачи является квадратное уравнение вида х²-(x₁+х₂)х+(х₁х₂)= 0 или х²-bx+c= 0. Для простоты потребуем от обучаемого вводить первый член квадратного трехчлена в виде Х*Х. В различных вари­антах задачи значения элементов 1, 2, 3, 7, 8, 12, 13 постоян­ны, а значения элементов 5, 6, 10, 11 изменяются и равны значениям b и с, как и элементов 4 и 9, являющиеся знаками чисел b и с. В условиях задачи значения b и с могут быть одно- или двухразрядными целыми числами, поэтому каждо­му из этих чисел отводится по два элемента.

После вычисления b=-(х₁+х₂) и с =(х₁х₂) необходи­мо элементам W 4, 5, 6 и 9, 10, 11 присвоить значения соответ­ственно b и с вместе с их знаками. Если b>0, то элементу 4 строки присвоим символ « + », в противном случае — сим­вол « — », а элементам 5 и 6 — значение переменной b. Аналогично поступить со знаком с, присвоив его элементу 9 пере­менной W, а элементам 10, 11 — значение с.

Если b или с являются одноразрядными числами, то в эталоне содержатся пробелы, что может привести к несо­впадению его с правильным ответом, поэтому необходимо удалить пробелы из эталона. Поскольку и ответ может со­держать пробелы, их также необходимо удалить. Чтобы не описывать процедуру удаления пробелов дважды, вынесем ее в подпрограмму.

После удаления пробелов из ответа и эталона осуще­ствляется их сравнение Если ответ и эталон представлены строковыми переменными, то они сравниваются целиком. Ес­ли же они хранятся в массивах А и W, то необходимо органи­зовать цикл, внутри которого ответ и эталон сравниваются поэлементно (последовательно, так как каждый символ явля­ется отдельным элементом массива) Посимвольное сравне­ние приведет к увеличению объема программы и усложнению схемы алгоритма, однако оно позволит установить позицию несовпадения ответа с эталоном и тем самым даст информа­цию о причине ошибки

Рассмотрим случай сравнения ответа с эталоном, пред­ставленным строковыми переменными.

Если совпадения не происходи т, то увеличи­вается на единицу количество попыток ответить на данный вопрос L. Количество неправильных ответов на данный вопрос n₂, общее количество ответов n₁, а количество правильных ответов k, данных подряд, считается равным нулю. Затем проверяется условие n₂<2, при выполнении которого обучае­мому выдается сообщение об ошибке и предлагается снова ответить на этот же вопрос. Если n₂≥2, то осуществляется анализ ответа обучаемого по частям

Если ответ и эталон совпали, то проверяется условие L= 0 (т. е. правильный ответ дан с первой попытки), т. е, на единицу увеличиваются количество правильных отве­тов По, данных с первой попытки, и количество правильных ответов k, данных с первой попытки подряд. В противном случае значения n₀ и k не изменяются. Затем проверяется условие k < 3, если оно выполняется, то выдается сообщение о правильности ответа, изменяется на единицу общее количе­ство ответов n₁ и осуществляется переход к новому заданию. Если k≥3, то общее количество заданий п принимает значе­ние i и осуществляется выход из цикла.

Анализ ответа обучаемого по частям осуществляется следующим образом. Обучаемому предлагается первый до­полнительный вопрос: «Введите коэффициент при X в первой степени В». После этого значение В сравнивается со значени­ем b, вычисленным в программе (сравнение удобнее вести в числовой форме). Если ответ и эталон совпадают, то пред­лагается второй дополнительный вопрос, в противном случае выясняется, что ошибка вызвана неправильным вычислением значения коэффициента b (о чем дается сообщение обучаемо­му), при этом изменяются значения n₁ и n₂ на единицу и пред­лагается исправить ошибку и снова ответить на этот же вопрос. Цикл повторяется до тех пор, пока не будет получен правильный ответ или обучаемый не попросит помощи.

Аналогично анализируется ответ на второй дополнитель­ный вопрос. После получения правильных ответов на оба дополнительных вопроса обучаемому выдается сообщение о правильности, изменяется на единицу значение n₁ и осуще­ствляется переход к следующему основному заданию.

Алгоритм решения задачи должен предоставлять обучае­мому возможность потребовать помощи в любой момент, когда диалоговая программа ожидает ввода отчета обучаемо­го. Для вызова помощи обучаемому необходимо ввести букву «П» Анализ ответа обучаемого в алгоритме осуществляется сравнением с символом «П». Если совпадения не происходит, то продолжается анализ ответа обучаемого описанным выше способом. Если совпадение происходит, то обучаемому выво­дится информация, которую автор программы определил как помощь обучаемому. Например, если обучаемый потребует помощи в ответ на основной вопрос, то в качестве сообщения можно выдать информацию о том, как, зная корни уравнения, определить коэффициент b и свободный член с квадратного уравнения. Если же он потребует помощи при ответе на первый дополнительный вопрос, то сообщение может содер­жать информацию о том, что коэффициент b равен сумме корней уравнения, взятой с обратным знаком, а при ответе на второй дополнительный вопрос — что свободный член равен произведению корней уравнения.

Выход из цикла, определяющего номер основного вопро­са, возможен двумя способами: 1) при получении подряд трех правильных вопросов (k≥3), в этом случае n = i, где i — номер последнего вопроса, на который отвечал обучаемый; 2) естественным образом, после того как цикл будет выполнен 10 раз, в это случае n=10.

Обработка статистических данных в этом примере со­стоит в накоплении значений переменных n, n₀, n₁ и определе­нии оценки обучаемого по результатам контроля. Определе­ние значений n, n₀ и n₁ приводилось выше. При определении оценки необходимо организовать разветвляющийся алгоритм, в ветвях которого проверяется выполнение условий:

n=n₀; n-n₀≤2; n-n₀≤4.

В конце цикла работы обучаемому можно вывести со­общение о числе вопросов, на которые он отвечал, о числе правильных ответов с первой попытки, о числе попыток отве­тить на вопросы.

Подпрограмма, предназначенная для удаления пробелов из ответа и эталона, может быть построена по следующему алгоритму.

Организуем цикл по i, который должен выполняться 15 раз (выбрано по количеству символов в ответе или эталоне плюс два пробела). Этот цикл просматривает все символы ответа или эталона и сравнивает их с символом пробела. Если происходит совпадение для k-го элемента, то элементы, на­чиная с (k+l)-гo до последнего, переписываются на место элементов, начиная с k-гo.

Если эталон и ответ обучаемого хранятся в символьном массиве, то необходимости в подпрограмме, предназначенной для удаления пробелов, нет, так как анализ ответа и эталона осуществляется посимвольно и каждый раз, когда в них будут появляться символы « », необходимо их удалять, как это делалось в подпрограмме, либо игнорировать и брать для анализа следующий символ.

Схема алгоритма решения представлена на рис. 1. Блок 2 задает начальные значения n, n₀, n₁ и k, равные нулю. Блок 4 задает начальное значение строковой переменной W, предназначенной для хранения эталона. Блок 3 организует цикл по номеру вопроса i, блок 5 задает начальные значения L и n₂, равные нулю. Блоки 6 к 8 осуществляют обращение к подпрограмме для получения равномерно распределенных случайных чисел y₁ и y₂ в диапазоне [0, 1], а блоки 7 и 9 вы­числяют значения случайных чисел х₁ и х₂ в диапазоне [—9,9]. Блок 10 вычисляет значение коэффициента b при х в первой степени и свободного члена с. Блок 11 проверяет знак переменной b и записывает в 4-ю позицию эталона символы « + » или « — » (блоки 12, 13), а блок 14 записывает в позиции 5 и 6 число, соответствующее b, в символьной форме. Блоки 15, 16, 17, 18 выполняют те же действия, что и блоки 11, 12, 13, 14, но только для переменной с. Блок 19 осуществляет обращение к подпрограмме для удаления пробелов из эталона, блок 23 — из ответа обучаемого, кото­рый перед этим вводится с помощью блока 22. Блок 24 про­веряет, не является ли ответ обучаемого обращением за помощью: если «да», то ему выдается сообщение 2 (блок 25), содержащее помощь, и далее осуществляется переход к блоку 28, в противном случае с помощью блока 26 производится анализ ответа обучаемого. Если ответ не совпадает с этало­ном, то увеличиваются на единицу значения n₁ и n₂, при­сваивается k значение ноль (блок 28), проверяется с по­мощью блока 30 условие, что данный ответ является первым неправильным ответом на данный вопрос. Если это условие выполняется, то выводится сообщение 4 (блок 36) и осуще­ствляется возврат к тому же заданию (к блоку 21), а в про­тивном случае — переход к анализу ответа по частям, кото­рый начинается с блока 32.

Если условие A = W (блок 26) выполняется, т. е. ответ правильный, то с помощью блока 27 проверяется условие L = 0 (ответ правильный с первой попытки). Если это условие выполняется, то по и k увеличиваются на единицу (блок 29) и далее осуществляется переход к блоку 31. Если условие не выполняется, то сразу осуществляется переход к блоку 31, который проверяет условие k≥3 (было получено подряд три правильных ответа). При выполнении условия п получает значение i-гo номера текущего основного вопроса (блок 35) и осуществляется переход к обработке статистических дан­ных (к блоку 47). Если условие k≥ 3 не выполняется, то обучаемому выдается сообщение 3, подтверждающее пра­вильность ответа (блок 33), осуществляется переход к блоку 34, увеличивающий значение n₁ на единицу, и далее переход к блоку 3 для выполнения действий над следующим основным заданием.

Обработка ответа по частям начинается с выдачи со­общения 5 (текста первого дополнительного вопроса) с по­мощью блока 32. Блок 37 осуществляет ввод ответа на этот вопрос. Блок 38 осуществляет анализ правильности ответа. Если ответ правильный, то осуществляется переход к следую­щему дополнительному вопросу (блок 39). В противном случае выдается сообщение 7, указы­вающее причину ошибки, изменяют­ся значения n₁ и n₂ на единицу и осуществляется переход к блоку 32 (возврат к тому же вопросу)

Аналогично с помощью блоков 39, 41, 43, 44, 45 производится ана­лиз ответа на второй дополнитель­ный вопрос.

Блоки 47, 48, 49, 50, 51, 52, 53 определяют оценку обучаемого, по­лученную по результатам контроля, и выводят сообщение о ней Блок 54 выводит заключительное сообщение, в котором указывается: число вопро­сов, на которые отвечал обучаемый n; число вопросов, на которые он ответил правильно с первой попытки n₀; число сделанных попыток отве­тить на вопросы n₁. На этом цикл работы с диалоговой программой заканчивается.

Далее приведена схема алгорит­ма, реализованного в подпрограмме, предназначенной для удаления про­белов из ответа обучаемого и эта­лона.

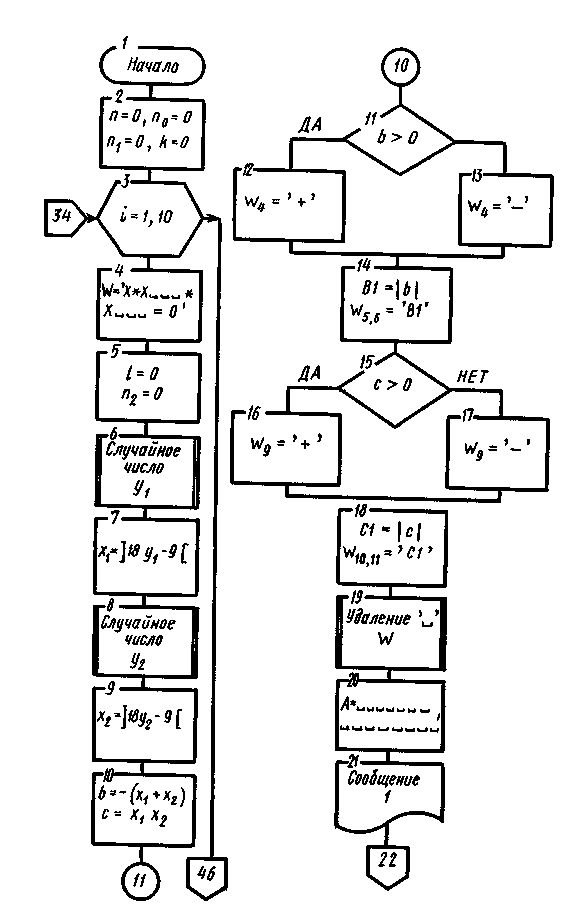
Рисунок 1

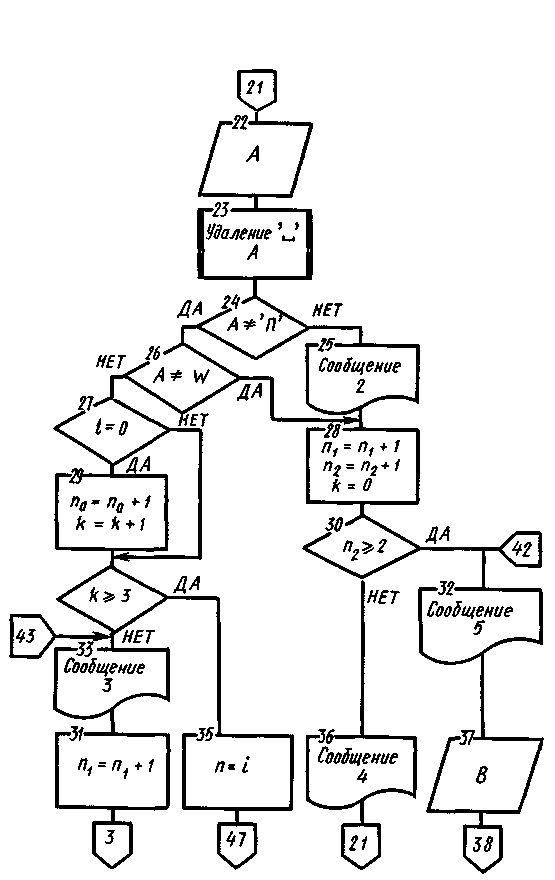
Рисунок 1 (продолжение)

Рисунок 1 (продолжение)

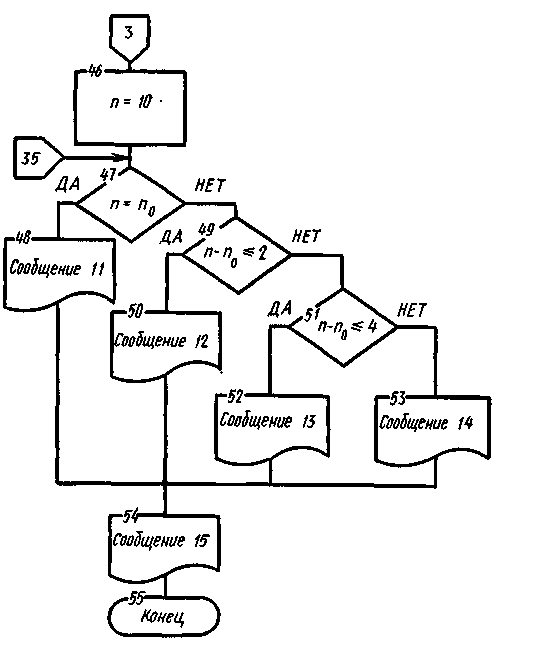
Рисунок 1 (продолжение)

Рисунок 1 (продолжение)

Программа, реализующая алгоритм, представленный на рис.1 на языке ПАСКАЛЬ:

PROGRAM LR14(INPUT,OUTPUT);

LABEL 5,10,15,2O,25,3O,35,45,5O;

CONST NV=10; NA=l5;

TYPE ST=STRING[NA];