Фпм

1 Вопрос

Абсолютной погрешностью измерения называют разность между найденным на опыте х_i и

истинным значением х₀ физической величины:

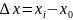, где i=1,2,…,n

Относительная погрешность – это погрешность, выраженная в долях

истинного значения измеренной величины

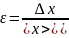
2 Вопрос

По природе возникновения погрешности делятся на систематические и случайные. Систематические погрешности подразделяются на приборные, методические и погрешности метода обработки данных.

Систематической погрешностью измерения называется составляющая погрешности измерения, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины. Например, шкала измерительной линейки неравномерна, капилляр

термометра имеет в различных участках различный диаметр, весы неравноплечные, стрелка амперметра при отсутствии тока не стоит на нуле и прочие. Систематическую погрешность измерения эксперименТально можно обнаружить либо сопоставлением данного результата с результатом измерения этой же величины, но полученным другим методом, либо путем использования более точных средств измерений. Однако обычно систематические погрешности оценивают путем теоретического анализа условий измерения, основываясь на известных

свойствах средств измерений

Приборные погрешности.

Точность измерения любого измерительного прибора ограничена. Погрешности приборов, предназначенных для производственных целей (амперметров, вольтметров, потенциометров и т.д.) определяются их классами точности. Класс точности обычно выражается в процентах. Например, амперметр с классом точности 0,2% определяет полное значение тока, соответствующего полной шкале, с погрешностью, не превышающей 0,2%. Конечно, это – максимальная погрешность. В научных работах принято указывать среднеквадратичную погрешность, поскольку относительная погрешность измеряемой величины зависит от положения стрелки.

Методические погрешности.

К таким погрешностям относятся, например, погрешности методики измерения. Например, неучет силы трения вала при определении момента инерции диска динамическим методом или проверка реальной жидкостью (водой) уравнения Бернулли, полученного для идеальной жидкости.

Погрешности методики обработки результатов.

Они возникают вследствие неправильной или несовершенной методики при определении искомой величины путем вычислений и при определении самих погрешностей.

При увеличении числа измерений систематические погрешности не уменьшаются. Для их уменьшения используются более точные приборы и наиболее совершенные методики измерения и обработки данных.

Случайные погрешности - это составляющие погрешности измерения, изменяющиеся случайным образом при повторных измерениях одной и той же величины. К ним можно отнести, наряду со случайными изменениями напряжения в электросети, температуры в лаборатории и др., факторы, связанные с несовершенностью органов чувств человека и его навыковых качеств. В

процессе измерения значение и знак случайной погрешности не остаются постоянными. Чтобы

уменьшить случайную погрешность, нужно:

1) уменьшить влияние внешних факторов;

2) проводить измерения внимательно и тщательно;

3) увеличить число опытов

Грубые погрешности (промахи) – погрешности измерения, существенно превышающие

ожидаемую при данных условиях. Они возникают вследствие недосмотра экспериментатора или

неисправности аппаратуры

3 вопрос: Функция плотности вероятности обладает следующими свойствами:

- симметрична относительно <х>,

- достигает максимального значения в точке <х>,

- быстро стремится к нулю , когда | х_i-<х>| становится большим по сравнению с σ .

4 вопрос

сигма -стандартное отклонение.

При малом σ кривая уже, а максимум выше, что соответствует более доброкачественным измерениям, то есть малому отклонению соответствует более доброкачественное измерение.

5 вопрос

Средней квадратичной погрешностью отдельного результата измерения :

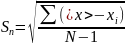
средняя квадратичная погрешность среднего арифметического:

-

Доверительный интервал 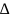х можно рассчитать по формуле:

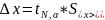
где коэффициент Стьюдента и находится из таблиц коэффициента Стьюдента

Конечный результат, в данном случае, представляется в виде:

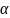при =К%

6 вопрос.

Вероятность случайного события определяется пределом отношения числа случаев благоприятных для данного события к общему числу наблюдении при

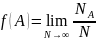
7 вопрос

Разобьем весь набор результатов измерений на интервалы. Из всех N измерений выберем минимальное и максимальное значения x_min и x_max . Число интервалов К будет равно частному от деления

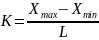
где L – шаг интервала.

Шаг интервала в данной работе должен быть целым числом и выбираться так, чтобы число интервалов было не меньше 8 и не больше 20. Нумеруются интервалы следующим образом:

1 – интервал [x_min/( x_min+ L)],

2 – интервал [( x_min+ L)/ /( x_min+2 L)],

3 – интервал [( x_min+ 2L)/ ( x _min+ 3L)],

k – интервал [(x_min + (k -1)L)/(x_min + kL)] .

Если на оси абсцисс отложить номера интервалов, а по оси ординат - число измерений, результаты которых попадают в данный интервал n_i, то получится эмпирический график

распределения числа измерений по интервалам, называемый гистограммой .

При большом числе измерений отношение n_i /N характеризует вероятность появления

значений измеряемой величины в данном интервале с шагом L. Если n_i /N разделить на величину шага интервала L, то значение величины y_i=n_i/NL будет характеризовать относительное число благоприятных случаев в единичном интервале. Диаграмма, построенная для y_i, показывает распределение плотности вероятности по интервалам и называется приведенной гистограммой.

Форму приведенной гистограммы, получаемой при небольшом числе опытов, нельзя предсказать заранее. Но теория вероятности позволяет вычислить форму предельной гладкой кривой, к которой стремятся гистограммы при неограниченном увеличении числа опытов. Эта предельная

кривая носит название кривой Гаусса Распределение, соответствующее предельной кри-

вой, называют нормальным (гауссовым) распределением.Оно описывается функцией распределения:

где σ²– как уже сказано выше, является дисперсией, σ -

характеризует разброс измерений относительно средне-

арифметического значения и называется стандартным

отклонением или среднеквадратичной погрешностью.

Функция Гаусса является нормированной, т.е. f(x)

удовлетворяет соотношению:

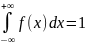
Интеграл имеет бесконечные пределы. Это означает, что измеряемая величина с вероятностью 1 (или 100%) лежит в пределах от 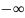до , или то, что нахождение измеряемой величины в этих пределах является событием достоверным. Функция плотности вероятности обладает следую-

щими свойствами :

- симметрична относительно <х>,

-достигает максимального значения в точке <х>,

- быстро стремится к нулю, когда |хi-<х>| становится

большим по сравнению сs .