Выполнил: студент гр. 1221
Бикмурзин Р.Ш.
Проверил: доцент
Абрамова В.В.
Лабораторная работа №6.
Решение задач целочисленного программирования (ЗЦЛП)
План выполнения работы:
Решить ЗЦЛП методом ветвей и границ. Дать графическую иллюстрацию этапов решения.
Сравнить результаты решения ЗЦЛП этими методами.
Оформить отчёт по работе, который должен содержать решения ЗЦЛП двумя методами, графические иллюстрации решений с полученными отсечениями, выводы, ответы на контрольные вопросы.
Контрольные вопросы:
Какие задачи относятся к ЗЦЛП?
Главная идея метода ветвей и границ.
Этапы решения ЗЦЛП методом ветвей и границ. Правила ветвления.
Геометрическая иллюстрация отсечений проведённых по методу ветвей и границ.
Задача.
F = x1 + x2 min
Решаем задачу методом ветвей и границ:
После решения задачи симплекс-методом без требований целочисленности переменных получаем такие результаты:
Решение задачи методом ветвей и границ:
;
;
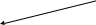
Решение задачи 2:
;
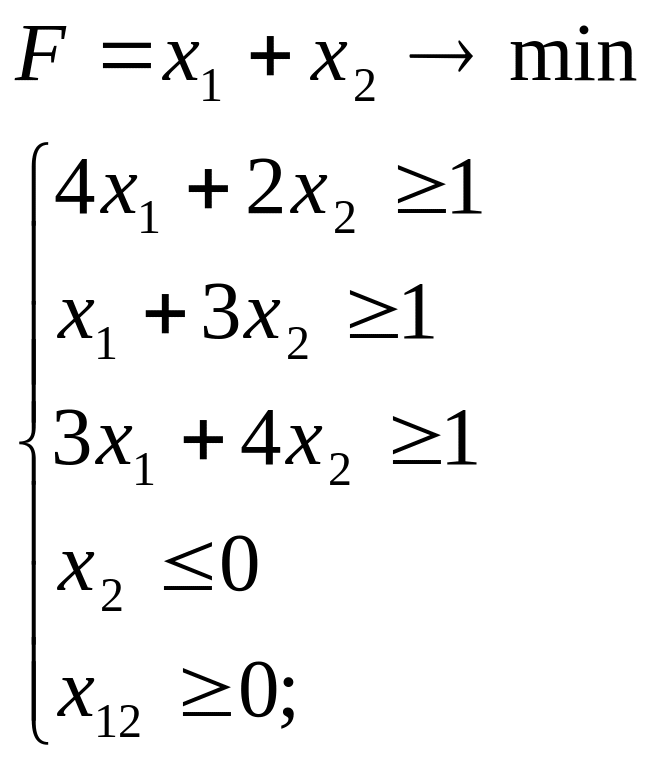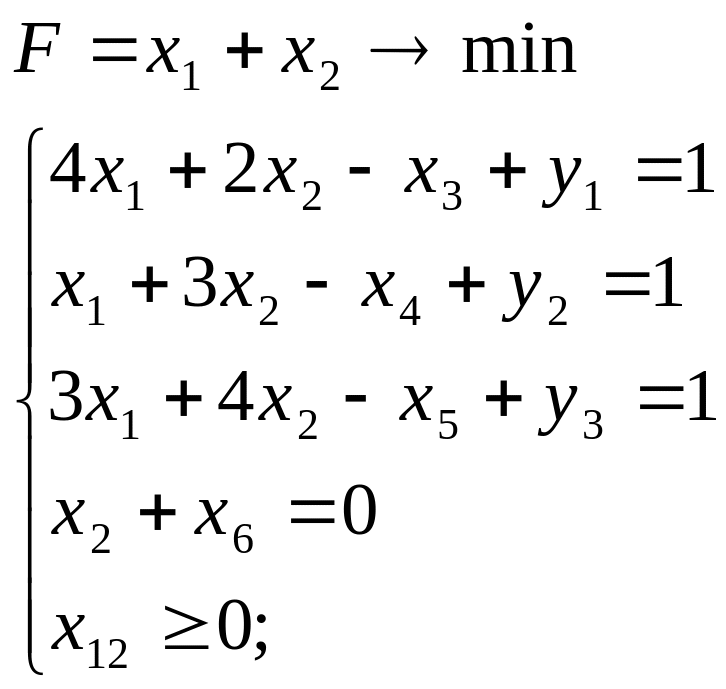Решаем эту
систему:
Базис |
b |
x 1 |
x 2 |
x 3 |
x 4 |
x 5 |
x 6 |
у 1 |
у2 |
у 3 |
|
у1 |
1 |
4 |
2 |
-1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
у2 |
1 |
1 |
3 |
0 |
-1 |
0 |
0 |
0 |
1 |
0 |
|
у3 |
1 |
3 |
4 |
0 |
0 |
-1 |
0 |
0 |
0 |
1 |
|
x6 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
F |
-3M |
-8M+1 |
-9M+1 |
M |
M |
M |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Базис |
b |
x 1 |
x 2 |
x 3 |
x 4 |
x 5 |
x 6 |
у1 |
у 2 |
у 3 |
|
у1 |
1 |
4 |
0 |
-1 |
0 |
0 |
-2 |
1 |
0 |
0 |
|
у2 |
1 |
1 |
0 |
0 |
-1 |
0 |
-3 |
0 |
1 |
0 |
|
у3 |
1 |
3 |
0 |
0 |
0 |
-1 |
-4 |
0 |
0 |
1 |
|
x2 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
F |
-3M |
-8M+1 |
0 |
M |
M |
M |
9M-1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Базис |
b |
x 1 |
x 2 |
x 3 |
x 4 |
x 5 |
x 6 |
у1 |
у 2 |
у 3 |
|
x1 |
1/4 |
1 |
0 |
-1/4 |
0 |
0 |
-1/2 |
1/4 |
0 |
0 |
|
у2 |
3/4 |
0 |
0 |
1/4 |
-1 |
0 |
-5/2 |
-1/4 |
1 |
0 |
|
у3 |
1/4 |
0 |
0 |
3/4 |
0 |
-1 |
-5/2 |
-3/4 |
0 |
1 |
|
x2 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
F |
-M-1/4 |
0 |
0 |
-M+1/4 |
M |
M |
5M-1/2 |
2M-1/4 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Базис |
b |
x 1 |
x 2 |
x 3 |
x 4 |
x 5 |
x 6 |
у1 |
у 2 |
у 3 |
|
x1 |
1/3 |
1 |
0 |
0 |
0 |
-1/3 |
-4/3 |
0 |
0 |
1/3 |
|
у2 |
2/3 |
0 |
0 |
0 |
-1 |
1/3 |
-5/3 |
0 |
1 |
-1/3 |
|
x3 |
1/3 |
0 |
0 |
1 |
0 |
-4/3 |
-10/3 |
-1 |
0 |
4/3 |
|
x2 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
F |
-2/3M-1/3 |
0 |
0 |
0 |
M |
-1/3M+1/3 |
5/3M+1/3 |
M |
0 |
4/3M-1/3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Базис |
b |
x 1 |
x 2 |
x 3 |
x 4 |
x 5 |
x 6 |
|
|||
x1 |
1 |
1 |
0 |
0 |
-1 |
0 |
-3 |
|
|||
x5 |
2 |
0 |
0 |
0 |
-3 |
1 |
-5 |
|
|||
x3 |
3 |
0 |
0 |
1 |
-4 |
0 |
-10 |
|
|||
x2 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
|||
F |
-1 |
0 |
0 |
0 |
1 |
0 |
2 |
|
|||
Решение
оптимально.
Решение Задачи 3:
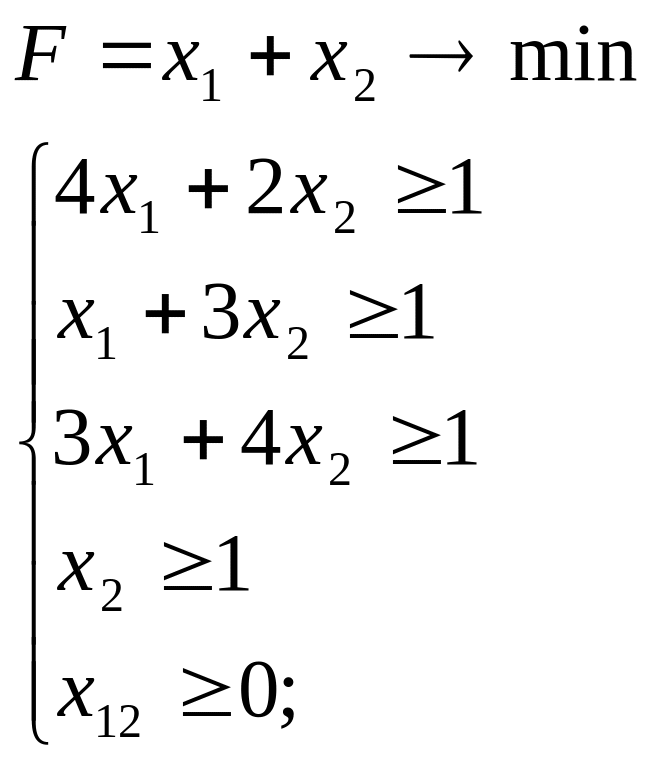
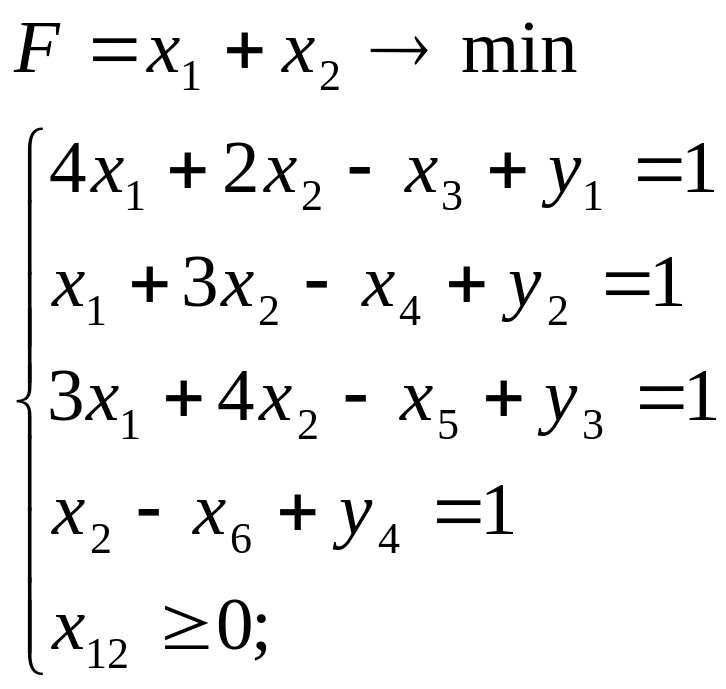Решаем эту систему:
Базис |
b |
x 1 |
x 2 |
x 3 |
x 4 |
x 5 |
x 6 |
y1 |
y 2 |
y3 |
y 4 |
|
y1 |
1 |
4 |
2 |
-1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
y2 |
1 |
1 |
3 |
0 |
-1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
y3 |
1 |
3 |
4 |
0 |
0 |
-1 |
0 |
0 |
0 |
1 |
0 |
|
y4 |
1 |
0 |
1 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
1 |
|
F |
-4M |
-8M+1 |
-10M+1 |
M |
M |
M |
M |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Базис |
b |
x 1 |
x 2 |
x 3 |
x 4 |
x 5 |
x 6 |
y1 |
y 2 |
y3 |
y 4 |
|
y1 |
1/2 |
5/2 |
0 |
-1 |
0 |
1/2 |
0 |
1 |
0 |
-1/2 |
0 |
|
y2 |
1/4 |
-5/4 |
0 |
0 |
-1 |
3/4 |
0 |
0 |
1 |
-3/4 |
0 |
|
x2 |
1/4 |
3/4 |
1 |
0 |
0 |
-1/4 |
0 |
0 |
0 |
1/4 |
0 |
|
y4 |
3/4 |
-3/4 |
0 |
0 |
0 |
1/4 |
-1 |
0 |
0 |
-1/4 |
1 |
|
F |
-3/2M-1/4 |
-1/2M+1/4 |
0 |
M |
M |
-3/2M+1/4 |
M |
0 |
0 |
5/2M-1/4 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Базис |
b |
x 1 |
x 2 |
x 3 |
x 4 |
x 5 |
x 6 |
y 1 |
y2 |
y 3 |
y 4 |
|
y1 |
1/3 |
10/3 |
0 |
-1 |
2/3 |
0 |
0 |
1 |
-2/3 |
0 |
0 |
|
x5 |
1/3 |
-5/3 |
0 |
0 |
-4/3 |
1 |
0 |
0 |
4/3 |
-1 |
0 |
|
x2 |
1/3 |
1/3 |
1 |
0 |
-1/3 |
0 |
0 |
0 |
1/3 |
0 |
0 |
|
y4 |
2/3 |
-1/3 |
0 |
0 |
1/3 |
0 |
-1 |
0 |
-1/3 |
0 |
1 |
|
F |
-M-1/3 |
-3M+2/3 |
0 |
M |
-M+1/3 |
0 |
M |
0 |
2M-1/3 |
M |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Базис |
b |
x 1 |
x 2 |
x 3 |
x 4 |
x 5 |
x 6 |
y 1 |
y 2 |
y3 |
y 4 |
|
x1 |
1/10 |
1 |
0 |
-3/10 |
1/5 |
0 |
0 |
3/10 |
-1/5 |
0 |
0 |
|
x5 |
1/2 |
0 |
0 |
-1/2 |
-1 |
1 |
0 |
1/2 |
1 |
-1 |
0 |
|
x2 |
3/10 |
0 |
1 |
1/10 |
-2/5 |
0 |
0 |
-1/10 |
2/5 |
0 |
0 |
|
y4 |
7/10 |
0 |
0 |
-1/10 |
2/5 |
0 |
-1 |
1/10 |
-2/5 |
0 |
1 |
|
F |
-7/10M-2/5 |
0 |
0 |
1/10M+1/5 |
-2/5M+1/5 |
0 |
M |
9/10M-1/5 |
7/5M-1/5 |
M |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Базис |
b |
x 1 |
x 2 |
x 3 |
x 4 |
x 5 |
x 6 |
y 1 |
y2 |
y3 |
y4 |
|
x4 |
1/2 |
5 |
0 |
-3/2 |
1 |
0 |
0 |
3/2 |
-1 |
0 |
0 |
|
x5 |
1 |
5 |
0 |
-2 |
0 |
1 |
0 |
2 |
0 |
-1 |
0 |
|
x2 |
1/2 |
2 |
1 |
-1/2 |
0 |
0 |
0 |
1/2 |
0 |
0 |
0 |
|
y4 |
1/2 |
-2 |
0 |
1/2 |
0 |
0 |
-1 |
-1/2 |
0 |
0 |
1 |
|
F |
-1/2M-1/2 |
2M-1 |
0 |
-1/2M+1/2 |
0 |
0 |
M |
3/2M-1/2 |
M |
M |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Базис |
b |
x 1 |
x 2 |
x 3 |
x 4 |
x 5 |
x 6 |
|
||||
x4 |
2 |
-1 |
0 |
0 |
1 |
0 |
-3 |
|
||||
x5 |
3 |
-3 |
0 |
0 |
0 |
1 |
-4 |
|
||||
x2 |
1 |
0 |
1 |
0 |
0 |
0 |
-1 |
|
||||
x3 |
1 |
-4 |
0 |
1 |
0 |
0 |
-2 |
|
||||
F |
-1 |
1 |
0 |
0 |
0 |
0 |
1 |
|
||||
Решение
оптимально:
Геометрическая иллюстрация отсечений:
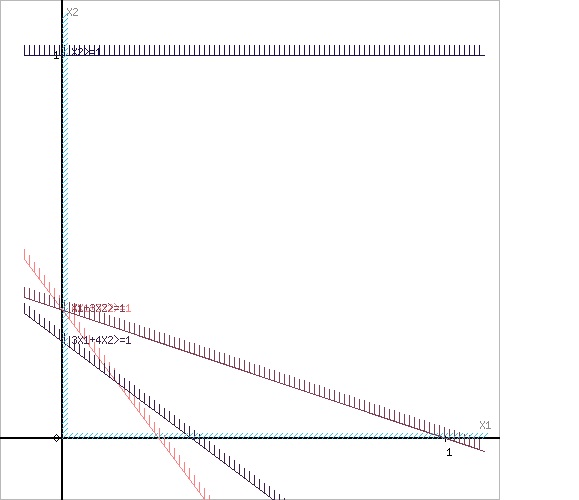
Ответы на контрольные вопросы: