Свойствоплоскостейуровня:

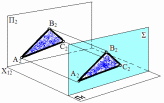Прямаяилифигура,лежащаявплоскостиуровняпроецируетсябезискажениянатуплоскостьпроекций,которойданнаяплоскостьуровняпараллельна (рис. 39).

Рис.39

2.Проецирующиеплоскости–этоплоскости,перпендикулярныетолькооднойизплоскостейпроекций.

а)Горизонтальнопроецирующаяплоскость –этоплоскость,перпендикулярнаяП_{1(рис. 40).}

Рис.40

Свойствопроецирующейплоскости:

Всеплоскиегеометрическиефигуры,принадлежащиекгоризонтальнопроецирующейплоскости,проецируютсянагоризонтальныйследданнойплоскостиввидеотрезкапрямой(рис.40б,в).

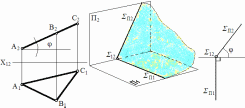б) Фронтально проецирующая плоскость – это плоскость,перпендикулярнаяП_{2(рис. 41).}

Рис.41

в) Профильно проецирующая плоскость – это плоскость,перпендикулярная П_{3(рис. 42).}

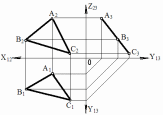Рис.42

5. Признакпринадлежноститочкиипрямойплоскости

Теорема1 : Прямая принадлежитплоскости,еслионапроходитчерездветочки, принадлежащиеэтойплоскости(рис.43).

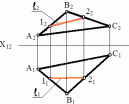Рис.43

Теорема2:Точкапринадлежит плоскости,еслионарасположенанапрямой, лежащейвданнойплоскости(рис. 44).

Рис.44

3.6.Главныелинии плоскости

Извсехпрямых,которыемогутбытьпроведенывплоскости,следуетвыделить главныелинии,ккоторымотносятся:

1. Горизонталь плоскости – прямая, принадлежащая заданной

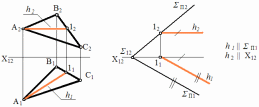плоскостии,параллельнаягоризонтальнойплоскостипроекцийП_1(рис.45).

Рис.45

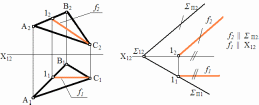2. Фронталь плоскости – прямая, принадлежащая заданнойплоскостии,параллельнаяП_2(рис.46).

Рис.46

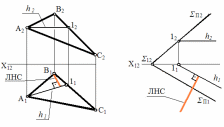3. Линиянаибольшегоската(ЛНС)–этопрямая,перпендикулярнаякгоризонталиплоскостиисоставляющаямаксимальныйуголсплоскостьюП₁₍рис.47).

Рис.47

4. Линиянаибольшегонаклона(ЛНН)–этолиния,перпендикулярнаякфронталиплоскостиисоставляющаямаксимальныйуголсплоскостью П₂(рис.48).

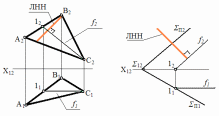
Рис.48

4.Преобразованиечертежа

Раздел4

Вначертательнойгеометриизадачирешаютсяграфически.Количествоихарактергеометрическихпостроений,приэтом,определяютсянетолькосложностьюзадачи,ноивзначительнойстепенизависятоттого,скакимипроекциями(удобнымиилинеудобными)приходитсяиметьдело.Приэтомнаиболеевыгоднымчастнымположениемгеометрическогообъектаследуетсчитать:

• положение, перпендикулярное к плоскости проекций (длярешенияпозиционных,а врядеслучаев,иметрическихзадач);

• положение,параллельноепоотношениюкплоскостипроекций(прирешенииметрическихзадач).

Следуетотметить,чтоприрешенииметрическихзадач,связанных

сопределениемистинныхразмеровизображенныхнаэпюрефигур,могутвстретитьсязначительныетрудности,еслизаданныепроекциинеподвергнуть специальнымпреобразованиям.

Почти любая задача начертательной геометрии решается

значительнопроще,еслихотябынекоторыеиззаданныхгеометрическихэлементовзанимаютвпространствечастноеположение(параллельныилиперпендикулярныплоскостямпроекций).Поэтомуприрешенииметрическихзадач,связанныхсопределениемнатуральныхвеличинрасстояний,угловисамихгеометрическихэлементов,возникаетнеобходимостьпреобразованиячертежей,т.е.измененияих.Этопозволяетперевестигеометрическийэлементизобщегоположениявчастное,прикоторомонпроецируетсянаплоскостипроекцийбез искажения.

Существуютследующиевидыпреобразованиячертежа:

1. способзаменыплоскостейпроекций;

2. способвращения;

3. способплоскопараллельногоперемещения;

В нашемкурсемырассмотримдвапервыхспособа.