2. Параллельноепроецирование

Рис.3

ЕслицентрпроекцийS–бесконечноудаленнаяточка,товсепроецирующиелучипараллельнымеждусобой.ДляпроведенияэтихлучейзадаетсянаправлениепроецированияS^∞.

Нарис.3показанопостроениепараллельнойпроекциикривойℓ₁₍А₁,В₁,С₁)наплоскостьП₁.Параллельныелучиобразуютцилиндрическую поверхностьΣ.

Всвоюочередь,параллельноепроецированиеделитсяна2вида,которыезависятотугланаклонапроецирующихлучейкплоскости

проекций:

А)прямоугольноеилиортогональноепроецирование

Рис.4

Каждый из лучей лежит относительно плоскости П₁ подуглом90^0(рис.4).

Б)косоугольноепроецирование

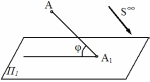Рис.5

φ-уголнаклонапроецирующеголучакплоскостипроекцийП₁

Прикосоугольномпроецированиипроецирующиелучисоставляютсплоскостью проекцийугол,неравный90° .

2. Общиесвойствапроецирования

1. Проекциейточкиявляетсяточка.

2. Проекциейпрямойлинии–прямая(частныйслучай:проекцияпрямой–точка,еслипрямаяпроходитчерезцентрпроекций).

3. Еслиточкавпространстве инцидентна(принадлежит)линии,

топроекцияэтойточкипринадлежитпроекцииданнойлинии.Дляпараллельногопроецированияхарактерныещедвасвойства:

• Проекции параллельных прямых, такжепараллельны.

• Отношение длин параллельных отрезков равныотношениюдлиних проекций:

|АВ| _ |А₁В₁|

|СD| ¯ |С₁D₁|

Каждыйизрассматриваемыхспособовпроецированияимеетсвоипреимуществаинедостатки.Взависимостиоттого,длякакойцеливыполняетсячертеж, используетсятот илиинойспособ.

Для выполнения чертежа, по которому изготовляется

изображаемыйпредмет, используетсяортогональноепроецирование.

Косоугольное,параллельноепроецированиеиспользуется,восновном,дляполученияаксонометрическихизображений,центральное–дляпостроенияперспективныхизображений.

Визучаемомкурсеосновноевниманиебудетуделеноортогональномупроецированию.

2. Ортогональныепроекции(прямоугольныепроекцииилиметодМонжа)

Проецированиенаоднуплоскостьпроекцийдаетизображение,котороенепозволяетоднозначноопределитьформуиразмерыизображенногопредмета.ПроекцияточкиА(рис.6)неопределяетположениесамойточкивпространстве,таккакнеизвестно,накакоерасстояниеонаудаленаотплоскостипроекцийП₁.ЛюбаяточкапроецирующеголучаS,проходящегочерезточкуА,будетиметьсвоейпроекциейточкуА₁, т.е.А_1≡В_1≡С_1≡D₁.

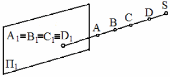Рис.6

Наличиеоднойпроекциисоздаетнеопределенностьизображения.Втакихслучаяхговорятонеобратимостичертежа,таккакпотакомучертежуневозможновоспроизвестиоригиналгеометрическогообраза.Решениеэтойзадачиявляетсяосновнойвтехническойпрактике.Так,напроизводствеизделиеизготавливаютпоегопроекционнымчертежам,которыедолжныполностьюопределятьразмерыиформыэтогоизделия.Чертеждолженбыть“обратимым”,т.е.вполнеопределяющимпроецируемыегеометрическиеобразы(объекты).

Дляисключениянеопределенностиизображения,аппаратпроецированияудваивается,т.е.создаетсяещеоднаплоскость

проекцийП_{2и еще}одинцентрпроецированияS_2(рис.7).ПересечениепроецирующихлучейсплоскостямиП_1иП_{2определяют}проекцииточкиА(А_1иА₂).Такимобразом,полученнаяпараточекА_1иА_{2является}модельюточкиАвпространстве(илиизображением).РасстояниеАА_1-высотаточкиА,АА_2-глубинаточкиА.

Вэтомслучаечертежявляетсяобратимым,иможноопределитьположениеточкиАвпространстве.

Итак,сущностьметодаортогональногопроецированиязаключаетсявтом,чтопредметпроецируетсянадвевзаимноперпендикулярныеплоскостилучами,ортогональными(перпендикулярными)кэтимплоскостям.

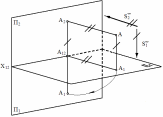Х_12–линияпересеченияплоскостейП_1–горизонтальнаяплоскость

проекций.

П_2–фронтальнаяплоскостьпроекций.

А_{1–горизонтальная}проекцияточки.А_2–фронтальнаяпроекцияточки.

Рис.7

Для реализации данного метода, необходимы следующиеусловия:

1) П₁ П₂;

2) S₁^∞П₁;

3) S₂^∞П_2.

Чтобыполучитьплоскийчертеж(эпюрМонжа),состоящийизуказанныхвышепроекций,плоскостьП_{1совмещают}вращениемвокругосиХ_12сплоскостьюП_2(рис.7).Проекционныйчертеж,накоторомплоскостипроекцийсовсемиизображенияминаних,совмещеныопределеннымобразомоднасдругой,называетсяэпюром(отфранц.еpure-чертеж)(рис.8).Заменивнаглядноеизображениеэпюром,мыутратилипространственнуюкартинурасположенияплоскостейпроекцийиточки.Ноэпюробеспечиваетточностьиудобоизмеряемостьизображенийпризначительнойпростотепостроений.

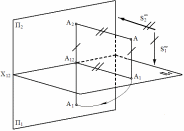ПритакомспособесовмещенияплоскостейП_{1и П2},проекцииА_1иА_{2окажутся}расположенныминаодномперпендикулярекосиХ₁₂.Прямыелинии,соединяющиеразноименныепроекцииточкинаэпюре,называютсялиниямипроекционнойсвязи,которыевсегдадолжныбытьперпендикулярныкоси.

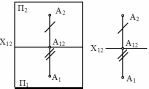
Рис.8