7. Изображениеплоскости

Плоскостьвпроекцияхсчисловымиотметкамиизображаетсяизадаетсятемижеопределителями,чтоивортогональныхпроекциях,аименно:

• тремяточками,нележащиминаоднойпрямой(рис.117);

Рис.117

• прямойиточкой,нележащейнаэтойпрямой(рис.118);

Рис.118

• двумяпараллельнымиилипересекающимисяпрямыми(чертежисм.выше);

• проекциямиплоскойфигуры(рис. 119).

Рис.119

Нообычновпроекцияхсчисловымиотметкамиплоскостьзадаетсямасштабомуклона∑_i–этопроградуированнаяпроекциялиниинаибольшегоскатаплоскости.Еговыделяют2-мяпараллельнымипрямыми(тонкойитолстой)иобозначаютбуквойсиндексом∑_i.

Итак,нарис.120изображенаплоскость∑,пересекающаяплоскостьуровняП_0полинии∑₀.Вплоскости∑проведеналинияскатаMNипостроенаеепроекцияmnнаплоскостьП_0.УголφмеждупрямойMNиеепроекциейmnопределяетуголнаклонаплоскости∑кплоскостиуровняП₀.

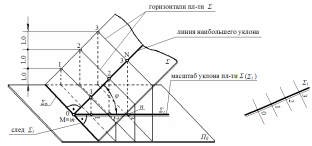
Рис.120

Проградуируемлиниюскатаповысоте,дляэтогопроведемгоризонтальныелинии,которыедолжныбытьперпендикулярныклиниискатаMN.

Спроецируемгоризонталинапроекциюmn,онидолжныбытьпараллельныследу∑_0.

Итак,плоскость∑задананачертежемасштабомуклонов∑_i,которая,какговорилосьвыше,изображаетсяввиде2-хпараллельныхпрямых,однаизкоторыхв2-3разатолщедругой,игоризонталей,перпендикулярныхкмасштабууклонов.

Проекция mn линии ската MN с нанесенными на ней

интерваламиявляетсямасштабомуклонаплоскости∑иобозначается,вданномслучае,∑_i.

Угломпаденияплоскости∑называютугол,образованныйданнойплоскостью∑иплоскостью П₀.

Иногда,особенноприрешенииинженерныхзадачнаместности,

требуетсяопределить положениеплоскостипоотношениюксторонамсвета.Втакомслучаевводитсяпонятиеуглапростиранияплоскости.

Поднаправлениемпростиранияпринимаютправоенаправлениегоризонталей,еслисмотретьнаплоскостьвсторонувозрастаниячисловыхотметок.

Угол,составленныйземныммеридианоминаправлениемпростиранияназываетсяугломпростирания(ψ)иявляетсяазимутомэтихлиний.Этотуголотсчитываетсяотсеверногоконцамеридианапротивчасовойстрелкидонаправленияпростирания.

Углыпаденияипростираниянаходятширокоеприменениевгеологиикакэлементы,характеризующиезалеганиепластагорной

породывтолщеземнойкоры.

Задача1.ЧерезточкуА_{7провести}плоскость∑сугломпадения

=35^0иугломпростиранияψ=135^{0(рис. 121)}.

Решение:

Рис.121

Вершинойуглапростиранияможетбытьлюбаяточкачертежа,втомчисле иточкаА.ЧерезпроекциюА_{7данной}точкипроведемземноймеридиан«север–юг»иподугломψ=135^0–прямуюлинию(направлениепростирания),котораябудетявлятьсягоризонтальюискомойплоскости,имеющейотметку7.Впроизвольномместеподпрямымугломкэтойгоризонталипроведемлиниюмасштабауклонов

искомойплоскости∑_i.Дляградуированиямасштабауклонов,т.е.дляопределенияинтервалаℓплоскости,построимпрямоугольныйтреугольниксоднимкатетом,равнымединицедлины(заданногомасштаба)ипротиволежащимуглом=35⁰.Второйкатетэтоготреугольникаибудетявлятьсяинтерваломℓ.

Илирассчитатьпоформуле: L_Р=1/tg.

Приградуированиимасштабауклоновпринято,чтовозрастание

отметокидетотнаблюдателявпередвытянутойвсторонуправойруки, совпадающейснаправлениемпростирания.