Вопрос 30. Использование метода эквивалентного генератора для работы нелинейной цепи.

Ответ: Если в сложной электрической цепи есть одна ветвь с нел. резист., то определить ток в ней можно методом эквивалентного генератора. Выделим ветвь с нел. резист., а всю остальную схему представим в виде активного двухполюсника. Этот 2-полюсник по отношению к зажимам a и b выделенной ветви можно представить в виде последовательного соединения источника ЭДС с E, равной напряжению на зажимах ab при разомкнутой ветви ab (Uabx), сопротивления, равного входному сопротивлению Rвх линейного 2-полюсника, и сопротивления ветви ab. Строим результирующую ВАХ пассивной части схемы – задаемся произвольным током (точка m), проводим через нее горизонталь и складываем отрезок mn, равный напряжению на нел. рез., с отрезком mp, равным напряжению на R: mn + mp = mq. Определяем ток в цепи: заданное значение ЭДС откладываем по оси абсцисс и через полученную точку проводим вертикаль до пересечения с результир. ВАХ в точке q. Ордината q равна току.

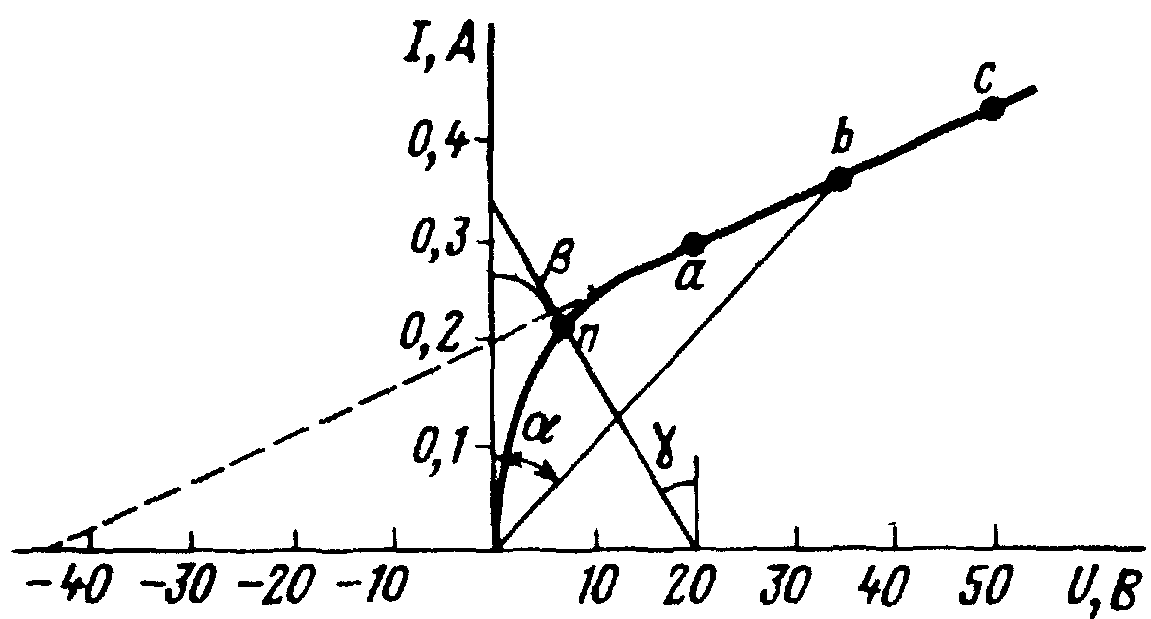
Вопрос 31. Статическое и динамическое сопротивления.

Ответ: Статическое сопротивление Rст. характеризует поведение нелин. резист. в режиме неизменного тока. Оно равно отношению напряжения на НР к протекающему по нему току: Rст=U/I. Также оно численно равно тангенсу угла α между осью ординат и прямой, идущей в точку b, умноженному на отношение масштабов по осям m_U/m_i. При переходе от одной точки ВАХ к соседней Rст изменяется. Динамическое сопротивление Rдин – отношение малого приращения напряжения dU на НР к соответствующему приращению тока dI: Rдин=dU/dI. Также оно численно равно тангенсу угла β наклона касательной к ВАХ в рабочей точке, умноженному на m_U/m_i. Оно характеризует поведение НР при достаточно малых отклонениях от предыдущего состояния. Если ВАХ НР имеет участок, где увеличению напряжения на ΔU соответствует убыль тока на ΔI, то Rдин отрицательно.

Вопрос 32. Общая характеристика методов анализа нелинейных цепей переменного тока.

Ответ: Методы анализа нел. цепей бывают: аналитические и графические. Аналитические в отличие от графических позволяют проводить анализ в общем виде, а не только для частных значений параметров. Недостаток этих методов – приходится выражать аналитически характеристики нелин. элементов, а это связано с погрешностью. Поэтому расчет производится лишь с известной степенью приближения. Методы анализа: 1) графический при использовании характеристик нелин. элементов для мгновенных значений; 2) аналитический при использовании характеристик нелин. элементов для мгновенных значений при их кусочно-линейной аппроксимации; 3) аналит. или графич. при использовании ВАХ по первым гармоникам; 4) аналит. или графич. при использовании ВАХ по действующим значениям несинусоидальных величин; 5) аналитич. путем расчета по первой и одной или нескольким высшим или низшим гармоникам; 6) с помощью линейных схем замещения; 7) малого параметра; 8) интегральных уравнений; 9) моделирования. Чем сложнее хар-р нел. явления, тем сложнее метод анализа.

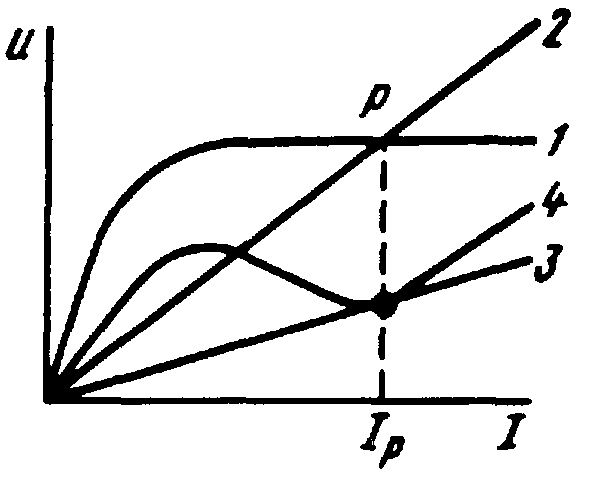
В опрос 33. Феррорезонанс напряжений.

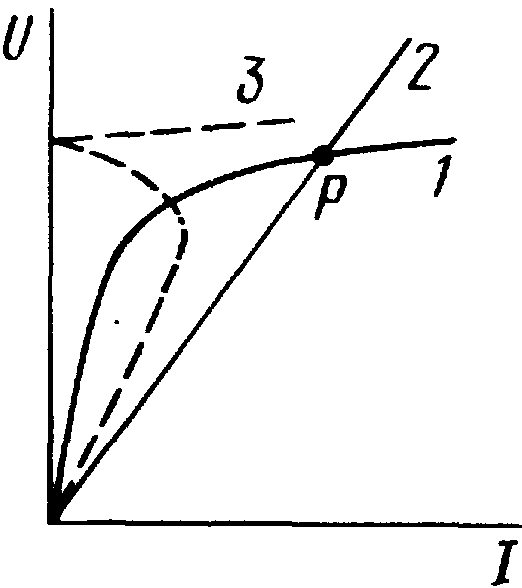
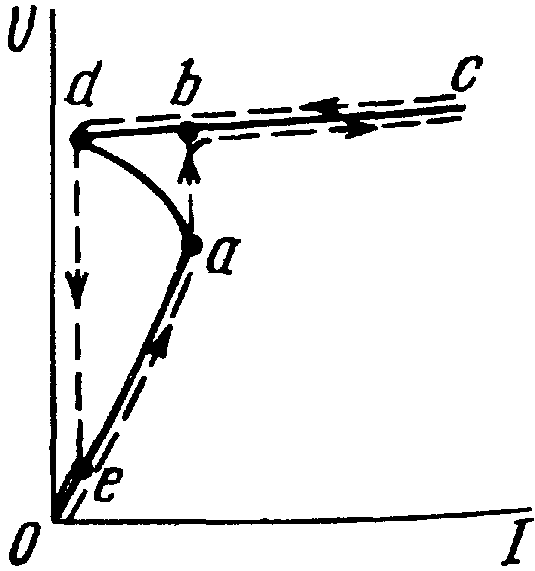
Ответ: Это режим работы последовательной цепи с нелинейной индуктивностью и линейной емкостью, при котором первая гармоника тока в цепи совпадает по фазе с напряжением U источника ЭДС. Феррорез. напряжений можно достичь путем изменения напряжения или частоты источника питания схемы, а также путем изменения емкости и параметров катушки со стальным сердечником. Феррорез. соответствует точке p на рисунке. Условие резонанса: X_L=X_C.

В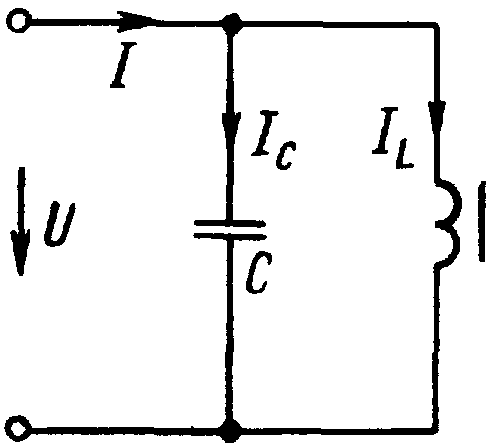 опрос 34. Феррорезонанс токов.

Ответ: Это режим работы параллел. цепи с нелин. индуктивностью и линейн. емкостью, при котором реактивная составляющая первой гармоники тока I_L равна току I_C. По 1-му закону Кирхгофа I=I_L+I_C. Так как токи I_L и I_C находятся в противофазе, то точке p соответствует режим феррорез. токов, т.е. I=0. Следует учитывать, что в феррорез. режиме (точка d) ток I в неразветвленной части схемы до нуля не снижается за счет высших гармоник и активной составляющей 1-й гармоники в токе I_L.

В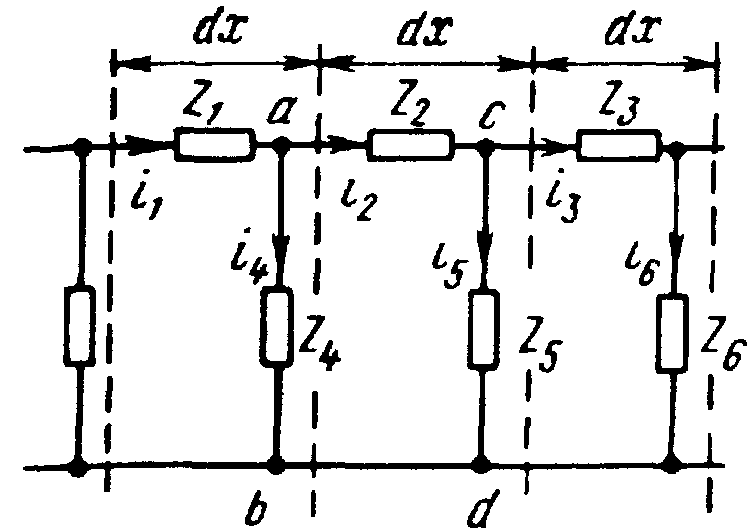 опрос 35. Линии с распределенными параметрами.

Ответ: Электрические линии с рас. пар. – линии, в которых для одного и того же момента времени i и U непрерывно изменяются при переходе от одной точки (сечения) линии к соседней точке, т.е. являются функциями времени и пространственной координаты. Это происходит, потому что линии обладают распределенными продольными и поперечными элементами. Магнитные линии с рас. пар. – линии, магнитный поток и магнитное напряжение вдоль которых непрерывно меняются при переходе от одной точки линии к соседней. Сопротивления Z₁, Z₂, Z₃ – продольные, Z₄, Z₅, Z₆ – поперечные. Из-за утечки тока через Z₄ ток i₂≠i₁. Линия однородная, если равны все продольные Z участков линии одинаковой длины и равны поперечные Z участков линии одинаковой длины. Линия неоднородная, если продольн. или поперечн. Z различны. В нелинейных линиях продольные или поперечные Z являются функциями протекающих по ним токов, а в линейных – не являются.

В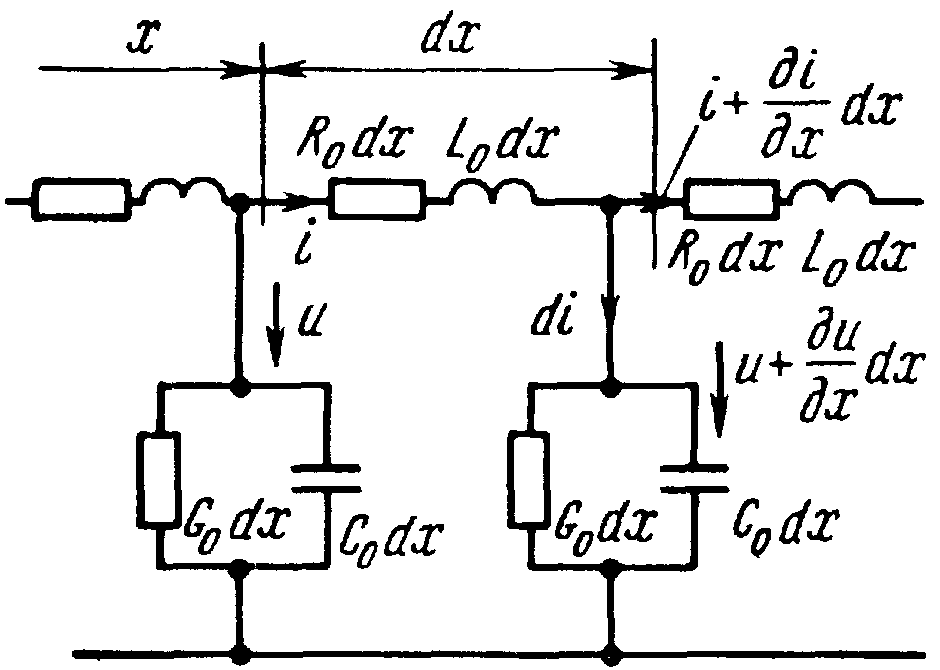 опрос 36. Составление дифференциальных уравнений для однородной линии с распределенными параметрами.

Ответ: Для единицы длины линии: R₀ – продольное активное сопротивление; L₀ – индуктивность; C₀ – ёмкость; G₀ – поперечная проводимость. Разобьем линию на участки длиной dx, где x – расст. от начала линии. Параметры на длине dx: R₀dx, L₀dx, G₀dx, C₀dx. Ток в начале рассматриваемого участка и напряжение между проводами – функции расстояния вдоль линии x и времени t. Составим уравнение по 2-му закону Кирхгофа для замкнутого контура, образованного участком длиной dx, обойдя его по часовой стрелке: . После упрощения: (ур.1). По 1-му закону Кирх.: . Ток di равен сумме токов через G₀dx и C₀dx: => . После подстановки: (ур.2). Уравнения 1 и 2 – искомые диф. уравнения.