Вопрос 10. Расчет переходного процесса при промежуточном режиме свободного процесса.

Ответ: Процесс разрядки. При R/(4L²) = 1/(LC) корни p₁ = р₂ = -R/(2L) – действительные, равные и кратные. Тогда , где А₁ и А₂ определяются по законам коммутации. Напряжение на ёмкости и ток во время предельного апериодического процесса: ;

Вопрос 11. Алгоритм расчета переходного процесса классическим методом.

Ответ: 1) Найти независимые начальные условия, то есть, напряжения на ёмкостях и токи на индуктивностях в момент начала переходного процесса. 2) Составить систему уравнений на основе законов Кирхгофа, Ома, электромагнитной индукции и т.д., описывающих состояние цепи после коммутации, и исключением переменных получить одно диф. уравнение, неоднородное относительно искомого тока или напряжения. Для простых цепей получается диф. уравнение I или II порядка, в котором в качестве искомой величины выбирают либо ток в индуктивном элементе, либо напряжение на емкостном элементе. 3) Составить общее решение полученного неоднородного диф. уравнения цепи в виде суммы частного решения неоднородного диф. уравнения (в установившемся режиме для электрических цепей) и общего решения соответствующего однородного диф. уравнения. 4) В общем решении найти постоянные интегрирования из начальных условий, т. е. условий в цепи в начальный момент времени после коммутации.

В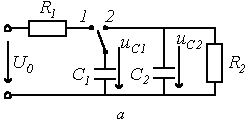 опрос 12. Обобщенные законы коммутации, пример цепей с переходными процессами с «некорректными» начальными условиями.

Ответ: Законы. 1) При переходе от t = 0_ до t = 0+ суммарное потокосцепление Σψ каждого замкнутого контура послекоммутационной схемы не должно претерпевать скачкообразных изменений. Суммарное потокосцепление – алгебраическая сумма произведений токов контура на индуктивности их индуктивных элементов. 2) При переходе от t = 0_ до t = 0+ суммарный заряд Σq на обкладках конденсаторов, присоединенных к любому узлу послекоммутационной схемы, должен остаться неизменным. Эти законы следуют из второго закона Кирхгофа.

Некорректные НУ связаны с некорректными коммутациями. Некорректные коммутации – такие, в которых корректный учет малых изменений параметров цепи может привести к невыполнению законов Кирхгофа.

П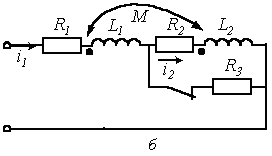 ри переводе в схеме а ключа из положения 1 в положение 2 трактование второго закона коммутации как невозможность скачкообразного изменения напряжения на конденсаторе приводит к невыполнению второго закона Кирхгофа . Аналогично при размыкании ключа в схеме б трактование первого закона коммутации как невозможность скачкообразного изменения тока через катушку индуктивности приводит к невыполнению первого закона Кирхгофа . Для данных схем, исходя из сохранения заряда и соответственно потокосцепления, можно записать:

Вопрос 13. Преобразования Лапласа. Основные определения.

Ответ: Суть использования преобразования: решение из области действительного переменного t переводится в область комплексного переменного p=a+jb, где р-оператор.

Диф. уравнение преобразуется в алгебраическое, проводится решение алгебраического уравнения, и затем осуществляется обратный переход в область действительного переменного t, т.е. находится решение f(t) - оригинала функции. F(p)-изображение. f(t)≈F(p). Переход f(t)→F(p) называется прямым преобразованием, для чего используется интеграл Лапласа F(p) = . Интегралы с бесконечным верхним пределом – несобственные. Свойства преобразования Лапласа: 1) Af(t)=AF(p), т.е. умножению оригинала на постоянную величину соответствует умножение изображения на ту же постоянную; 2) ∑f_k(t) = ∑F_k(p), т.е. сумме оригиналов соответствует сумма изображений.