- •Вопрос 1. Переходные процессы в линейных цепях. Определение переходных процессов, основные понятия.
- •Вопрос 2. Приведение задачи о переходном процессе к решению дифференциального уравнения с постоянными коэффициентами.
- •Вопрос 4. Характеристическое уравнение. Правило для записи характеристического уравнения.
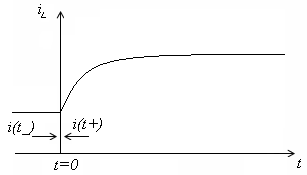
- •Вопрос 5. Законы коммутации, их обоснование.
- •Вопрос 6. Начальные условия переходных процессов. Независимые и зависимые начальные условия.
- •Вопрос 8. Расчет переходного процесса при апериодическом режиме.
- •Вопрос 9. Расчет переходного процесса при колебательном режиме.
- •Вопрос 10. Расчет переходного процесса при промежуточном режиме свободного процесса.
- •Вопрос 11. Алгоритм расчета переходного процесса классическим методом.
- •Вопрос 13. Преобразования Лапласа. Основные определения.
- •Вопрос 14. Преобразования Лапласа. Изображение первой производной.
- •Вопрос 15. Закон Ома в операторной форме.
- •Вопрос 16. Первый закон Кирхгофа в операторной форме.
- •Вопрос 19. Составление уравнений для изображений путем использования символического метода расчета синусоидальных цепей.
- •Вопрос 20. Последовательность расчета в операторном методе.
- •Вопрос 21. Использование интеграла Дюамеля для расчета переходных процессов. Переходная проводимость, переходная функция по напряжению.
- •Вопрос 22. Нелинейные цепи. Основные понятия, определения.
- •Вопрос 23. Примеры вольт-амперных характеристик некоторых нелинейных элементов.
- •Вопрос 24. Общая характеристика расчета нелинейных цепей.
- •Вопрос 25. Расчет нелинейной цепи при последовательном соединении элементов.
- •Вопрос 26. Расчет нелинейной цепи при параллельном соединении элементов.
- •Вопрос 30. Использование метода эквивалентного генератора для работы нелинейной цепи.
- •Вопрос 31. Статическое и динамическое сопротивления.
- •Вопрос 32. Общая характеристика методов анализа нелинейных цепей переменного тока.
- •Вопрос 37. Решение уравнений линии с распределенными параметрами при установившемся синусоидальном процессе. Постоянные интегрирования, постоянная распространения, волновое сопротивление.
- •Вопрос 38. Постоянная распространения и волновое сопротивление в некоторых частных случаях (постоянный ток, линия с малыми потерями).
- •Вопрос 39. Определение комплексов тока и напряжения в любой точке линии через напряжение и ток в начале линии.
- •Вопрос 40. Определение комплексов тока и напряжения в любой точке линии через напряжение и ток в конце линии.
- •Вопрос 46. Согласованная нагрузка.
- •Вопрос 52. Стоячие электромагнитные волны.
Вопрос 1. Переходные процессы в линейных цепях. Определение переходных процессов, основные понятия.
Ответ: Переходные процессы – процессы перехода от одного установившегося режима работы электрической цепи (обычно периодического) к другому (также периодическому), чем-либо отличающемуся от предыдущего, например амплитудой, фазой, формой или частотой, действующей в схеме ЭДС, значениями параметров схемы или вследствие изменения конфигурации цепи. Периодическими режимами являются синусоидального и постоянного тока, а также режим отсутствия тока в цепи. Коммутация – переключение электрической цепи (процесс замыкания или размыкания выключателей).
Вопрос 2. Приведение задачи о переходном процессе к решению дифференциального уравнения с постоянными коэффициентами.
О![]() твет:
Запишем уравнение по 2-му закону Кирхгофа
при замкнутом ключе. Сумма падений
напряжений на L и R равна ЭДС:
твет:
Запишем уравнение по 2-му закону Кирхгофа
при замкнутом ключе. Сумма падений
напряжений на L и R равна ЭДС:![]() или
или
![]() (дифференциальное уравнение). Определение
тока как функции времени является
решением диф. уравнения. Переходный
процесс описывается диф. уравнением:
неоднородным или однородным в зависимости
от того, содержит схема замещения
источники ЭДС и тока или нет. В линейной
цепи пер. процесс описывается линейными
диф. уравнениями, в нелинейной –
нелинейными. Методы расчета: классический,
операторный, интегралом Дюамеля,
пространства состояний.
(дифференциальное уравнение). Определение
тока как функции времени является
решением диф. уравнения. Переходный
процесс описывается диф. уравнением:
неоднородным или однородным в зависимости
от того, содержит схема замещения
источники ЭДС и тока или нет. В линейной
цепи пер. процесс описывается линейными
диф. уравнениями, в нелинейной –
нелинейными. Методы расчета: классический,
операторный, интегралом Дюамеля,
пространства состояний.
В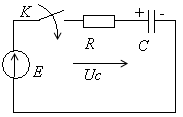
 опрос
3. Переходный процесс в цепи с конденсатором.
опрос
3. Переходный процесс в цепи с конденсатором.
Ответ: 1. Зарядка
конденсатора от источника постоянного
ЭДС через резистор. Переходный процесс
описывается неоднородным диф. уравнением
на основе 2-го закона Кирхгофа, закона
Ома и соотношения между током зарядки
и напряжением в конденсаторе:
![]() =>
=>
![]() ;
; ![]() ;
;
![]() ,
где
,
где
![]() ,
а
,
а
![]() .
Общее решение имеет вид:
.
Общее решение имеет вид:
![]() .
Для определения А обратимся ко 2-му
закону коммутации. Предположим, что до
замыкания ключа конденсатор не был
заряжен:
.
Для определения А обратимся ко 2-му
закону коммутации. Предположим, что до
замыкания ключа конденсатор не был
заряжен:
![]() => A
= -E.
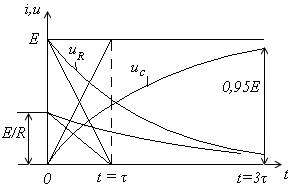
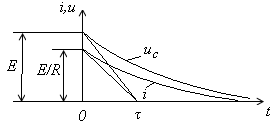
Напряжение во время зарядки:
=> A
= -E.
Напряжение во время зарядки:
![]() ,
где
,
где
![]() -
постоянная времени цепи. Зависимость
от t напряжения на конденсаторе определяет
зависимости от t зарядного тока и
напряжения на резисторе:
-
постоянная времени цепи. Зависимость
от t напряжения на конденсаторе определяет
зависимости от t зарядного тока и
напряжения на резисторе:
![]() ;
;
![]() .
.
2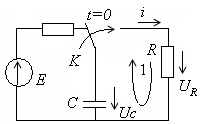
 .
Разрядка конденсатора через резистор.
После подключения конденсатора,
заряженного до напряжения
.
Разрядка конденсатора через резистор.
После подключения конденсатора,
заряженного до напряжения
![]() ,
ток в цепи будет обусловлен изменением
заряда q конденсатора:
,
ток в цепи будет обусловлен изменением
заряда q конденсатора:
![]() .
Составим диф. уравнение переходного
процесса в контуре 1:
.
Составим диф. уравнение переходного
процесса в контуре 1:
![]() .
.
Т.к. в цепи разрядки
конденсатора нет источника ЭДС, то диф.
уравнение – однородное:
![]() .
Так как до коммутации конденсатор был
не заряжен, то:
.
Так как до коммутации конденсатор был
не заряжен, то:
![]() =>
=>
![]() .
Разрядный ток:
.
Разрядный ток:
![]() .
.
Вопрос 4. Характеристическое уравнение. Правило для записи характеристического уравнения.
О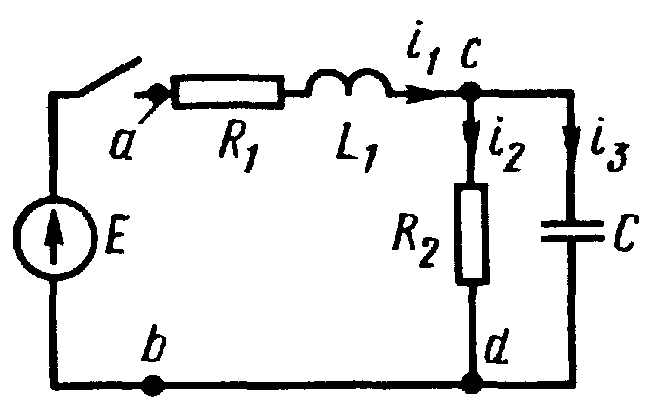
![]() твет:
Число алгебраических уравнений равно
числу неизвестных свободных токов. Для
нахождения p
решим систему относительно
твет:
Число алгебраических уравнений равно
числу неизвестных свободных токов. Для
нахождения p
решим систему относительно![]() :
:
![]() и
т.д. Т.к. в каждом определителе один из
столбцов будет состоять из нулей, то
и
т.д. Т.к. в каждом определителе один из
столбцов будет состоять из нулей, то
![]() ,
но каждый из свободных токов не может
быть равен нулю, поэтому определитель
Δ должен равняться нулю. Уравнение Δ =
0 называется характеристическим. Если
хар. уравнение имеет несколько корней,
то для каждого свободного тока (напряжения)
надо взять
,
но каждый из свободных токов не может
быть равен нулю, поэтому определитель
Δ должен равняться нулю. Уравнение Δ =
0 называется характеристическим. Если
хар. уравнение имеет несколько корней,
то для каждого свободного тока (напряжения)
надо взять
![]() .
Составление хар. уравнения путем
использования выражения для входного
сопротивления двухполюсника на переменном
токе. В схеме не должно быть магнитно-связанных
ветвей. Тогда
.
Составление хар. уравнения путем
использования выражения для входного
сопротивления двухполюсника на переменном
токе. В схеме не должно быть магнитно-связанных
ветвей. Тогда
![]() ;
jω
= р =>
;
jω
= р =>
![]() = 0, где Δ(р) – определитель системы
уравнений, составленный по методу
контурных токов.
= 0, где Δ(р) – определитель системы
уравнений, составленный по методу
контурных токов.