V2: Расчет на прочность при кручении
I: K=B
S: При проверочном расчете на прочность…
+:
-
Должно быть известно
Нужно определить
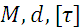
Проверить выполнение условия прочности
-:
-
Должно быть известно
Нужно определить
-:
-
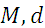
Должно быть известно
Нужно определить
-:
-
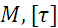
Должно быть известно
Нужно определить
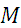
I: K=B
S: В скручиваемом стержне максимальные касательные напряжения действуют…
-: на III участке;
+: на I участке;
-: на II участке;
-: на I и II участке.
I: K=B
S: Если [τ] – допускаемое касательное напряжение, то из расчета на прочность, скручивающий момент…
+:
;
-:
;
-:
;
-:
.
I: K=B
S: Пусть 
– допускаемый угол поворота сечения
С,
- жесткость поперечного сечения на
кручение.
Тогда допускаемая величина M удовлетворяет неравенству…
+:
;
-:
;
-:
;
-:
.
I: K=B
S: Если [τ] – допускаемое касательное напряжение, то из расчета на прочность, диаметр вала…
+:
;
-:
;
-:
;
-:
.
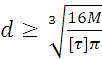I: K=B
S: Условие прочности для стержня имеет вид…
-:
-:
-:
+:
I: K=B
S: Если – допускаемое касательное напряжение, то из расчета на прочность диаметр вала…
+:
-:
-:
-:
V2: Расчет на жесткость при кручении
I: K=A
S: В процессе скручивания длина стержня L…
+: не изменяется;
-: сначала увеличивается, потом уменьшается;
-: увеличивается;
-: уменьшается.
I: K=B
S: Абсолютный угол закручивания стержня равен…
-:
;
-:
;
+:
;
-:
.
I: K=C
S: Пусть 
– жесткость поперечного сечения на
кручение.
Тогда максимальный относительный угол закручивания равен…
-:
;
-:
;
-: ;
+:
.
I: K=B
S: Взаимный угол поворота сечений A и B образца можно определить из формулы…
-:
;
-:
;
-:
;
+:
.
I: K=B
S: Известен взаимный угол поворота сечений A и B. Модуль сдвига материала образца можно определить из формулы…
+:
-:
-:
-:
I: K=B
S: Условие жесткости стержня при кручении имеет вид…
-:
;
-:
+:
;
-:
.
I: K=B
S: Условие прочности стержня при кручении имеет вид…
-: ;
-:
-: ;
+: .
I: K=C
S: Максимальный относительный угол закручивания имеет место на участке…
-:II
-:I и II
-:I
+:III
I: K=B
S: В скручиваемом стержне максимальные касательные напряжения действуют…
-: на III участке;
+: на I участке;
-: на II участке;
-: на I и II участке.
I: K=C
S: Пусть угол
поворота сечения С равен «
»
Тогда величина момента М вычисляется по формуле…
-:
-:
-:
+:
V1: Плоский прямой изгиб
V2: Поперечная сила и изгибающий момент и их эпюры
I: K=A
S: В сечении 1-1 имеют место внутренние силовые факторы …
-:
+:
-:
-:
I: K=B
S: В сечении 1-1 имеют место внутренние силовые факторы …
-:
+:
-:
-:
I: K=B
S: В сечении 1-1 имеют место внутренние силовые факторы …
-:
-:
-:
+:
I: K=B
S: В сечении 1-1 имеют место внутренние силовые факторы …
-:
-:
-:
+:
I: K=B
S: В сечении 1-1 имеют место силовые факторы:
+: 
;
-:
;
-:
;
-: 
.
I: K=A
S: В сечении 1-1 имеют место силовые факторы:
+: ;
-: ;
-:
;
-: 
.
I: K=A
S: В сечении 1-1 имеют место силовые факторы…
+: M=0, Q≠0
-: M=0, Q=0
-: M≠0, Q≠0
-: M≠0, Q=0
I: K=D
S: В сечении 1-1 имеют место силовые факторы…
+: M=0, Q=0
-: M≠0, Q≠0
-: M≠0, Q=0
-: M=0, Q≠0
I: K=B
S: В сечении 1-1 имеют место силовые факторы…
+: M=0, Q=0
-: M≠0, Q≠0
-: M≠0, Q=0
-: M=0, Q≠0
I: K=A
S: В сечении 1-1 имеют место силовые факторы…
+: M≠0, Q≠0
-: M≠0, Q=0
-: M=0, Q=0
-: M=0, Q≠0
I: K=C
S: В сечении 1-1 имеют место силовые факторы:
+: M=0, Q=0
-: M=0, Q≠0
-: M≠0, Q=0
-: M≠0, Q≠0
I: K=A
S: На тех участках балки, где распределенная нагрузка отсутствует:
+: поперечные силы постоянны, а изгибающие моменты меняются по линейному закону
-: поперечные силы равны 0
-: изгибающие моменты равны 0
-: эпюра изгибающих моментов изображается кривой линией
I: K=A
S: На тех участках балки, где действует распределенная нагрузка:
+: поперечные силы изменяются по длине балки: эпюры изгибающих моментов ограничены кривыми
-: изгибающие моменты изменяются по линейному закону
-: поперечные силы неизменны
-: изгибающие моменты неизменны
I: K=B
S: На тех участках балки, где поперечная сила имеет постоянное значение:
+: эпюра изгибающих моментов ограничена прямой линией
-: эпюра изгибающих моментов постоянна
-: эпюра изгибающих моментов носит убывающий характер
-: эпюра изгибающих моментов носит возрастающий характер
I: K=B
S: Для балки, снабженной шарниром, в шарнире
+: изгибающий момент равен 0
-: поперечная сила равна 0
-: изгибающий момент принимает экстремальное значение
-: поперечная сила минимальна
I: K=C
S: Любой скачок на эпюре изгибающих моментов равен:
+: сосредоточенному моменту, приложенному в этом сечении
-: поперечной силе, приложенной в этом сечении
-: сумме всех изгибающих моментов, приложенных к контуру
-: внешнему сосредоточенному моменту
I: K=C
S: Любой скачок на эпюре поперечных сил равен:
+: сосредоточенной силе, приложенной в этом сечении
-: сосредоточенному моменту, приложенному в этом сечении
-: сумме всех изгибающих моментов, приложенных к конструкции
-: сумме всех поперечных сил, приложенных к конструкции
I: K=A
S: На тех участках балки, где поперечные силы положительны…
+: изгибающий момент возрастает
-: изгибающий момент убывает
-: действует распределенный момент
-: изгибающий момент имеет постоянное значение
I: K=C
S: Статически неопределенная система изображена на рисунке…
+:
-:
-:
-:
I: K=A
S: Степень статической неопределенности рамы, изображенной на рисунке равна…
+: 1
-: 2
-: 3
-: 4
I: K=B
S: В сечении 1-1 имеют место внутренние силовые факторы…
-:
-:
-:
+:
I: K=В
S: В сечении 1-1 имеют место внутренние силовые факторы…
+:
-:
-:
-:
I: K=A
S: В сечении 1-1 имеют место внутренние силовые факторы…
-:
-:
-:
+:
I: K=B
S: В сечении 1-1 имеют место силовые факторы…
+: M≠0,Q≠0
-: M=0,Q≠0
-: M=0,Q=0
-: M≠0,Q=0
I: K=A
S: В сечении 1-1 имеют место силовые факторы…
+: M≠0,Q≠0
-: M=0,Q≠0
-: M=0,Q=0
-: M≠0,Q=0
I: K=B
S: В сечении 1-1 имеют место силовые факторы…
-: M≠0,Q≠0
-: M=0,Q≠0
-: M=0,Q=0
+: M≠0,Q=0
I: K=C
S: В сечении 1-1 имеют место силовые факторы…
+: M≠0,Q=0
-: M=0,Q≠0
-: M≠0,Q≠0
-: M=0,Q=0
I: K=C
S: В сечении 1-1 имеют место силовые факторы…
+: M≠0,Q≠0
-: M=0,Q≠0
-: M=0,Q=0
-: M≠0,Q=0
I: K=A
S: В сечении 1-1 имеют место силовые факторы…
+: M≠0,Q≠0
-: M=0,Q≠0
-: M=0,Q=0
-: M≠0,Q=0
I: K=A
S: В сечении 1-1 имеют место силовые факторы…
+: M≠0,Q≠0
-: M=0,Q≠0
-: M=0,Q=0
-: M≠0,Q=0
I: K=B
S: В сечении 1-1 имеют место силовые факторы…
+: M≠0,Q≠0
-: M=0,Q≠0
-: M=0,Q=0
-: M≠0,Q=0
I: K=B
S: Укажите эпюру поперечной силы в сечениях консольной балки…
-:
+:
-:
-:
I: K=B
S: Укажите эпюру изгибающего момента в сечениях консольной балки…
+:
-:
-:
-:
I: K=B
S: Эпюра поперечной силы в сечениях консольной балки…
+:
-:
-:
-:
I: K=B
S: Эпюра изгибающего момента в сечениях консольной балки…
-:
-:
+:
-:
I: K=B
S: N – продольная сила, Qy – поперечная сила, Mx – изгибающий момент
В плоских рамах возникают:
+: силовые факторы N, Qy, Mx
-: силовые факторы N, Qy
-: силовые факторы Qy, Mx
-: силовые факторы N, Mx
I: K=A
S: В сечении 1-1 имеют место силовые факторы:
+:N=0, Q≠0, M≠0
-: N≠0, Q≠0, M≠0
-: N=0, Q=0, M=0
-: N≠0, Q=0, M=0
I: K=A
S: В сечении 1-1 имеют место силовые факторы:
+: N=0, Q=0, M≠0
-: N=0, Q≠0, M=0
-: N≠0, Q≠0, M≠0
-: N=0, Q≠0, M≠0
I: K=C
S: В сечении 1-1имеют место силовые факторы:
+: N=0, Q=0, M≠0
-: N=0, Q≠0, M=0
-: N≠0, Q=0, M≠0
-: N≠0, Q≠0, M≠0
I: K= B
S: В сечении 1-1 имеют место силовые факторы:
+: N≠0, Q=0, M≠0
-: N=0, Q≠0, M≠0
-: N≠0, Q=0, M=0
-: N=0, Q=0, M≠0
I: K= B
S: В сечении 1-1 имеют место силовые факторы:
+: N=0, Q≠0, M≠0
-: N=0, Q=0, M≠0
-: N≠0, Q=0, M≠0
-: N≠0, Q≠0, M≠0
I: K= B
S: В сечении 1-1 имеют место силовые факторы:
+: N≠0, Q=0, M=0
-: N<>0, Q≠0, M=0
-: N=0, Q≠0, M≠0
-: N=0, Q=0, M≠0
I: K= B
S: В сечении 1-1 имеют место силовые факторы:
+: N≠0, Q=0, M=0
-: N≠0, Q≠0, M=0
-: N=0, Q=0, M≠0
-: N=0, Q≠0, M≠0
I: K=C
S: В сечении 1-1 имеют место силовые факторы:
+: N≠0, Q=0, M=0
-: N≠0, Q≠0, M=0
-: N=0, Q=0, M≠0
-: N=0, Q≠0, M=0
I: K=C
S: в сечении 1-1 имеют место силовые факторы
+: N≠0, Q≠0, M≠0
-: N≠0, Q=0, M=0
-: N=0, Q=0, M≠0
-: N=0, Q≠0, M≠0
I: K= B
S: в сечении 1-1 имеют место силовые факторы
+: N=0, Q=0, M=0
-: N=0, Q≠0, M≠0
-: N≠0, Q≠0, M≠0
-: N≠0, Q=0, M=0
I: K=A
S: в сечении 1-1 имеют место силовые факторы
+: N=0, Q=0, M=0
-: N=0, Q≠0, M≠0
-: N≠0, Q=0, M=0
-: N≠0, Q≠0, M≠0
I: K= B
S: в сечении 1-1 имеют место силовые факторы
+: N=0, Q=0, M=0
-: N=0, Q≠0, M≠0
-: N≠0, Q=0, M=0
-: N≠0, Q≠0, M≠0
I: K=C
S: в сечении 1-1 имеют место силовые факторы
+: N≠0, Q=0, M=0
-: N≠0, Q≠0, M=0
-: N=0, Q=0, M≠0
-: N=0, Q≠0, M≠0
I: K= B
S: в сечении 1-1 имеют место силовые факторы
+: N≠0, Q=0, M=0
-: N≠0, Q≠0, M=0
-: N=0, Q=0, M≠0
-: N=0, Q≠0, M≠0