V2: Перемещения и деформации

I: K=B

S: Изменение первоначальной длины стержня , обозначаемое , называется…

-: изменением формы стержня

-: деформацией

-: относительной линейной деформацией

+: абсолютным удлинением (укорочением)

I: K=С

S: Деформации (линейные и угловые) считаются практически малыми, если они не превосходят…

-: 0,12 (или 12%)

+: 0,05 (или 5%

-: 0,2 (или 20%)

-: 0,1 (или 10)

I: K=B

S: Оценка прочности элементов конструкций производится по наибольшему(ей) …

-: перемещению

-: усилию

-: деформации

+: напряжению

I: K=A

S: Перемещение точки в процессе деформации тела из одного положения в положение, бесконечно близкое к нему, называется…

+: линейным перемещением

-: деформированным состоянием

-: угловым перемещением

-: относительной деформацией

I: K=B

S: Предел отношения называется…

-: деформацией стержня

-: относительным изменением объема

-: абсолютной линейной деформацией

+: относительной линейной деформацией в точке ( )

I: K=B

S: При линейном напряженном состоянии Закон Гука выражается зависимостью…

-:

+:

-:

-:

I: K=A

S: Изменение линейных размеров тела и его частей…

+: линейная деформация

-: угловая деформация

-: относительная деформация

-: абсолютная деформация

I: K=B

S: Резонанс – это…

- : состояние колеблющейся систем, при котором максимальное напряжение цикла в опасной точке равно пределу прочности материала

- : состояние колеблющейся систем, при котором максимальное напряжение цикла в опасной точке равно пределу текучести материала

- : значительное уменьшение амплитуды колебаний из-за большой разницы частот вынужденных и собственных колебаний системы

+: многократное увеличение амплитуды колебаний в результате совпадения частот вынужденных и собственных колебаний системы

I: K=С

S: Материал называется анизотропным, если…

- : он имеет кристаллическую структуру

+: свойства образца, выделенного из материала, зависят от его угловой ориентации

-: он пластичный

-: свойства образца, выделенного из материала, не зависят от его угловой ориентации

V1: Растяжение и сжатие

V2: Продольная сила. Напряжения и деформации

I: K=B

S: Для стержня, схема которого изображена на рисунке,

нормальные напряжения, действующие в сечении 1-1, будут…

-: растягивающими и сжимающими

-: сжимающими

-: равны нулю

+: растягивающими

I: K=B

S: Для стержня, схема которого изображена на рисунке,

нормальные напряжения, действующие в сечении 1-1, будут…

-: растягивающими и сжимающими

-: растягивающими

-: равны нулю

+: сжимающими

I: K=B

S: Для стержня, схема которого изображена на рисунке,

деформации, возникающие в сечении 1-1, будут…

-: сжимающими

-: растягивающими и сжимающими

+: растягивающими

-: равны нулю

I: K=B

S: Для стержня, схема которого изображена на рисунке,

деформации, возникающие в сечении 1-1, будут…

-: сжимающими

+: растягивающими

-: растягивающими и сжимающими

-: равны нулю

I: K=B

S: Для стержня, схема которого изображена на рисунке,

деформации, возникающие в сечении 1-1, будут…

-: сжимающими

-: растягивающими и сжимающими

+: растягивающими

-: равны нулю

I: K=С

S: Чему равны напряжения в сечении I-I если P₁=20 кН, Р₂=5кН, а площадь поперечного сечения равна 510^-4 м²

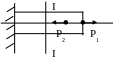
-: 40 МПа;

-: 10 МПа;

+: 30 МПа;

-: 50 МПа

I: K=С

S: Ступенчатый брус нагружен силами и ₁, действующими вдоль оси бруса. Левый конец бруса жестко закреплен. Площадь поперечного сечения правого участка бруса равна , а левого ₁=2 . Модуль упругости одинаков и равен . Если ₁=3 , то перемещение точки В будет определяться следующим соотношением:

-: ;

-: ;

-: ;

+: ;

I: K=A

S: Условие прочности при растяжении-сжатии …

-: ;

+: ;

-: ;

-: .

I: K=A

S: В поперечных сечениях бруса при центральном растяжении или сжатии возникают равномерно распределенные напряжения, равные отношению продольной силы к площади поперечного сечения. Что это за напряжения?

-: касательные

-: равнодействующие

+: нормальные

-: суммарные

I: K=B

S: Отношение относительной поперечной деформации к продольной, взятое по абсолютной величине называется

+: коэффициентом Пуассона

-: модулем упругости

-: модулем Юнга

-: коэффициентом скольжения

I: K=A

S: Обозначение внутреннего силового фактора при растяжении-сжатии…

-:

+:

-:

-:

I: K=A

S: Виды напряжений, возникающих при растяжении-сжатии…

-: касательные

+: нормальные

-: касательные и нормальные

-: деформированные

I: K=B

S: Параметр в формуле деформации …

-: Модуль сдвига

+: Модуль упругости

-: Модуль сопротивления

-: Модуль инерции

I: K=A

S: Условие прочности при растяжении-сжатии…

-:

+:

-:

-:

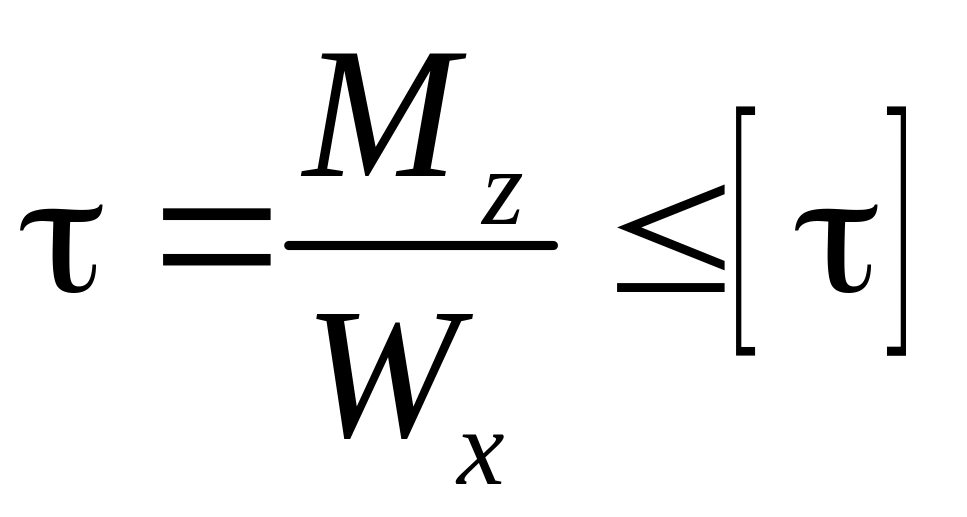
I: K=B

S: Закон Гука при растяжении-сжатии…

+:

-:

-:

-:

I: K=B

S: Укажите соответствующую нагружению стержня эпюру продольных сил в поперечных сечениях бруса(F – сосредоточенная нагрузка, q – распределенная нагрузка).

-:

-:

+:

-:

I: K=B

S: Укажите соответствующую нагружению стержня эпюру продольных сил в поперечных сечениях бруса(F – сосредоточенная нагрузка).

+:

-:

-:

-:

I: K=B

S: Укажите схему нагружения бруса соответствующую эпюре продольных сил (F – сосредоточенная нагрузка, q – распределенная нагрузка)....

+:

-:

-:

-:

I: K=B

S: Укажите соответствующую нагружению стержня эпюру продольных сил в поперечных сечениях бруса(F – сосредоточенная нагрузка, q – распределенная нагрузка).

+:

-:

-:

-:

I: K=B

S: Укажите соответствующую нагружению стержня эпюру продольных сил в поперечных сечениях бруса(q – распределенная нагрузка).

-:

+:

-:

-:

I: K=B

S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 2-2, будут…

-: растягивающими и сжимающими

-: растягивающими

+: равны нулю

-: сжимающими

I: K=B

S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 3-3, будут…

-: растягивающими и сжимающими

+: растягивающими

-: равны нулю

-: сжимающими

I: K=B

S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 3-3, будут…

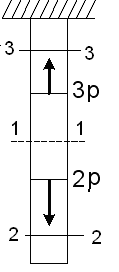
-: растягивающими и сжимающими

-: растягивающими

-: равны нулю

+: сжимающими

I: K=B

S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 3-3, будут…

-: растягивающими и сжимающими

+: растягивающими

-: равны нулю

-: сжимающими

I: K=B

S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 2-2, будут…

-: растягивающими и сжимающими

+: растягивающими

-: равны нулю

-: сжимающими

I: K=B

S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 1-1, будут…

-: растягивающими и сжимающими

+: растягивающими

-: равны нулю

-: сжимающими

I: K=B

S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 1-1, будут…

-: растягивающими и сжимающими

+: растягивающими

-: равны нулю

-: сжимающими

I: K=B

S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 2-2, будут…

-: растягивающими и сжимающими

+: растягивающими

-: равны нулю

-: сжимающими

I: K=B

S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 3-3, будут…

-: растягивающими и сжимающими

+: растягивающими

-: равны нулю

-: сжимающими

I: K=B

S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 3-3, будут…

-: растягивающими и сжимающими

-: растягивающими

-: равны нулю

+: сжимающими

I: K=B

S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 2-2, будут…

-: растягивающими и сжимающими

-: растягивающими

-: равны нулю

+: сжимающими

I: K=B

S: Для стержня, схема которого изображена на рисунке, нормальные напряжения, действующие в сечении 1-1, будут…

-: растягивающими и сжимающими

-: растягивающими

-: равны нулю

+: сжимающими