1.9. Транспортная задача в сетевой форме

В больших задачах по планированию перевозок массовых грузов решение ТЗ связано с большими трудностями, так как если количество станций отправления будет порядка несколько сотен, а количество станций назначения - тысячи, то соответствующая матрица тарифов будет содержать сотни тысяч элементов. Подготовка, хранение и преобразование в процессе вычислений столь обширной исходной информации - задача сложная, а порой и непреодолимая. В этом случае удобнее пользоваться ТЗ в сетевой форме. Дело в том, что реальные перевозки массовых грузов осуществляются по транспортным сетям, состоящим из участков, связывающих различные станции. Среди этих станций имеются станции отправления, назначения и участковые станции, через которые груз идет транзитом. Исходной информацией для расчета суммарных затрат на перевозки являются данные о затратах на перевозку единицы груза по каждому участку сети, количество которых лишь немногим отличается от количества связываемых станций. Следовательно, при тех же сотнях станций отправления и порядка тысячи станций назначения исходная информация будет содержать лишь две - три тысячи величин.

Положим, что имеющиеся станции отправления и назначения расположены на некоторой транспортной сети, состоящей из q участков связывающих между собой p станций. При этом нам удобно будет указанную сеть считать ориентированной. Это означает, что для дорог с двухпутным движением наряду с каждым участком a_t связывающим станцию i_t со станцией j_t, придется вводить еще участок , связывающий станцию = j_t со станцией = i_t .

Таким образом, транспортная сеть будет задана некоторым ориентированным графом

= (NA) , где N = , A = . (1.48)

Граф - основное понятие теории графов, математически определяется как совокупность двух множеств - множества элементов V и множе-

ства отношений между этими элементами E, обозначается G = (V, E).

Геометрически удобно изображать граф в виде схемы - тогда элементы множества V будут точками ( их называют вершинами V), а отношения E - отрезками, соединяющими элемент V_i с элементами, которые с ним связаны.

Граф называется ориентированным (орграфом G = (V, E)), если всякая пара точек Vi, Vj упорядочена, т. е. соединяющее их ребро имеет начало и конец, тогда оно называется дугой. Каждой вершине i = 1, p орграфа G сопоставляется вещественное число b_i. Если b_i > 0, то это означает, что вершина i отвечает пункту производства, в котором объем производства равен b_i. Если b_i < 0 , то соответствующая величина отвечает станции назначения с объемом потребления . Наконец, если b_i = 0, то это участковая станция, которую груз проходит транзитом. При этом будем полагать, что задача сбалансированная. План перевозок определяется выбором q - мерного вектора

X = ( x₁, x₂, ... , x_q ); (1.49)

x  0

с неотрицательными элементами, указывающими планируемые объемы перевозок по всем участкам сети.

Д ля каждой вершины i = 1, p орграфа G через обозначим множество тех дуг, для которых j_t = i, а через - множество тех дуг, для которых i_t = i.

Тогда при фиксированном плане перевозок (1.49) количество ввозимого и вывозимого груза в каждую станцию может быть определено по формуле

; ; i = . (1.50)

Это означает, что план перевозок (1.49) является допустимым, если он удовлетворяет условиям:

b_i = 0 , i = ; (1.51)

или

+ b_i = 0 , i = . (1.52)

Если , то это означает, что вершина i отвечает пункту производства, в котором объем производства равен .

Д алее, каждой дуге a_t , t = 1, q орграфа сопоставляется величина , указывающая затраты (тарифы), связанные с перевозкой единицы груза со станции i_t на станцию j_t по соответствующему участку сети.

Е сли , то α_t  α_t .

Задача состоит в нахождении такого допустимого плана перевозок (1.49), для которого достигается минимум суммарных транспортных издержек:

F = . (1.53)

Т аким образом, ТЗ в сетевой постановке можно сформулировать так: для фиксированного орграфа G при заданных величинах , b_{i ,} t = 1, q;

i = , удовлетворяющих условию баланса

,

определить q- мерный вектор (1.49), минимизирующий линейную функцию F = , при ограничениях (1.52).

Рассмотрим решение ТЗ в сетевой форме [6].

Пример. Требуется построить оптимальный план перевозки груза на сети от трех станций отправления до девяти станций назначения.

Станции отправления груза обозначим квадратами, а станции назначения - кружочками. Цифрами между станциями указано расстояние перевозки, а в знаменателе для звеньев 1-7, 1-11, 2-9, 3-10 заданы ограничения пропускной способности (рис. 1.11).

Решение.

ТЗ в сетевой форме начинают решать с составления начального плана, который не допускает встречных перевозок на участках заданного полигона. Начальный (или любой допустимый) план характеризуется определенным числом базисных звеньев: K = n - 1, где n - число вершин, вошедших в полигон сети.

Для полигона (рис. 1.11) число базисных звеньев равно:

K = 13 - 1 = 12.

Звенья с потоком, равным пропускной способности, являются небазисными. Эти потоки называют перенасыщенными. Изображать их будем пунктирной стрелкой.

При решении задачи может встретиться случай вырождения, когда число базисных звеньев заданного полигона меньше числа K. В этом случае по свободному звену (желательно по звену с наименьшим расстоянием) пропускают нулевой поток и это звено в последующих операциях принимают за базисное. Базисным может стать и звено с потоком, равным пропускной способности.

В ходе решения возможен и такой случай, когда число базисных звеньев в допустимом плане больше числа K, например, если на сети получился замкнутый контур. Это означает, что допущена ошибка, которую необходимо устранить до построения системы потенциалов. Для избежания данного случая рекомендуется снабжать потребителей только от одного поставщика, а от двух, когда у первого не хватит ресурсов.

Рис. 1.11

Возможный начальный план приведен в качестве примера на рис. 1.12, на котором знаком "+" отмечена вершина отправления груза, знаком "-" - вершина потребления (прибытия) на станции выгрузки, "- 40" - величина прибытия и "+ 200" - величина отправления груза. Поток на участке обозначен стрелкой в правопутном направлении, а величина грузопотока - числом у стрелки.

После построения начального (допустимого) плана, пример которого приведен на рис. 1.12, начинают строить на сети оптимальный план перевозок методом потенциалов. Любой допустимый план называют оптимальным тогда, когда вершине полигона могут быть присвоены некоторые числа (потенциалы) U и V, которые отвечают следующим условиям:

; для x_ij = 0 , (1.54)

; для 0 < x < d_ij , (1.55)

; для x = d_ij , (1.56)

где i, j - номера вершин полигона;

U_i, V_j - потенциалы соответственно i - й и j - й вершин;

C_ij - расстояние от i - й до смежной j - й вершины (длина участка, соединяющего соседние станции);

x_ij - грузопоток на звене ij;

d_ij - ограничение пропускной способности на участке ij.

Рис. 1.12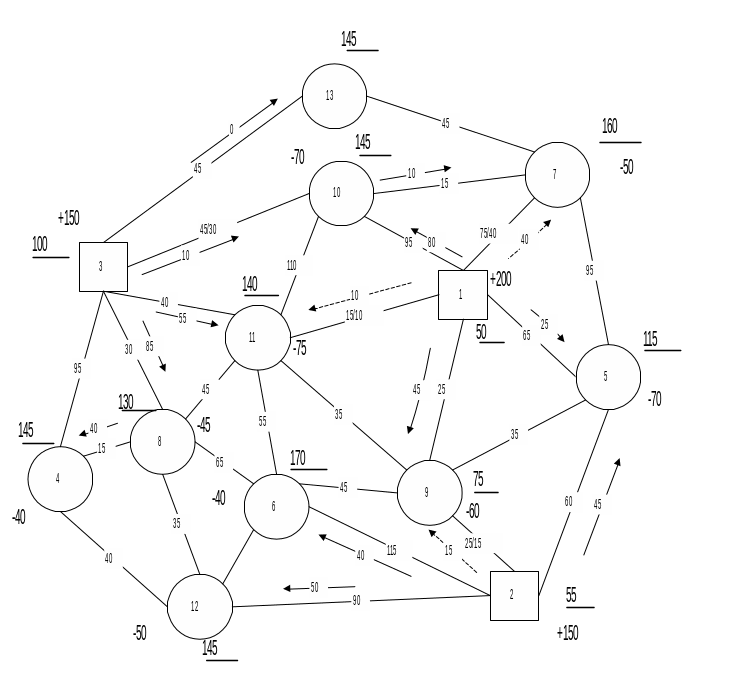

Для всех вершин полигона находят систему потенциалов. Какой-либо станции отправления присваивается начальный потенциал, например V3 = 100. Затем по базисным звеньям определяют потенциалы смежных вершин. Из условия оптимальности (1.49) следует, что

, (1.57)

если известен потенциал вершины i , а по звену походит грузопоток в направлении от i к j. Например, V₈ = U₃ + C_3.8 = 100 + 30 = 130.

Из этого же условия оптимальности следует, что

U_i = V_j + c_ij , (1.58)

если известен потенциал вершины j , а по звену проходит грузопоток в направлении от i к j. Например, U₂ = V₅ - C_5.2 = 115 - 60 = 55.

Потенциалы всех вершин заданного полигона на рис. 1.12 подчеркнуты.

После построения системы потенциалов находят звенья сети с нарушением оптимальности (1.54) и (1.56) по формуле

H_ij = V_j - U_i - c_ij . (1.59)

Для рассматриваемого примера имеются следующие нарушения условий оптимальности на свободных звеньях:

H_5.9 = 115 - 75 - 35 =5,

H_6.9 = 170 - 75 - 45 = 50.

Нарушения на звеньях с потоком, равным пропускной способности, отрицательны по своей величине:

H_2.9 = 75 - 55 - 25 = -5.

Из всех звеньев с нарушениями выбирают звено, имеющее максимальную по модулю величину нарушения. Для этого звена строят замкнутый контур, состоящий из базисных звеньев и выбранного звена с нарушением. Если замкнутый контур состоит из попутных звеньев без ограничения пропускной способности, то на звено с нарушением назначают поток улучшения плана

x_ул = min x_{ij встр}. (1.60)

На величину потока улучшения плана X_ул изменяют все потоки рассматриваемого контура: уменьшают встречные и увеличивают попутные потоки. Встречные и попутные потоки контура улучшенного плана находятся после определения направления следования потока на звене с нарушением. На рассматриваемом звене с нарушением, направления всегда будут от вершины с меньшим потенциалом, ограничивающей данное звено, к вершине с большим потенциалом, ограничивающей это звено с другой стороны. В направлении следования нового потока на свободном звене с нарушением просматриваются все потоки и из них находят попутные и встречные.

Если в замкнутом контуре есть попутные звенья с ограничением пропускной способности, то на звено с нарушением назначают поток

x_ул = min x_{ij встр} , (d_ij - x_ij)_попутн . (1.61)

Если звено с нарушением является перенасыщенным, то

x_ул = min x_{ij попутн} , (d_ij - x_ij)_встр . (1.62)

В контуре попутные потоки уменьшают, встречные - увеличивают.

Следует помнить, что контур улучшения плана всегда может быть только один для рассматриваемого звена с нарушением.

После этого пересматриваются потенциалы вершин, входящих в рассмотренный контур, и смежных с ним вершин.

Улучшенная схема вновь проверяется на оптимальность. Если небазисные звенья удовлетворяют условиям (1.54) и (1.56), то получен оптимальный план. Если небазисные звенья этому условию не удовлетворяют, то решение продолжают.

На рис. 1.13 приведен один из вариантов оптимального плана.

По формуле (1.59) были рассчитаны разности для перенасыщенных звеньев:

H_1.7 = 160 - 50 - 75 = +35;

H_1.11 = 140 - 50 - 15 = +75;

H_2.8 = 75 - 5 - 15 = +55.

Положительные разности на перенасыщенных звеньях говорят о перерасходе затрат. Недостаток пропускной способности звена I - II вызывает наибольший перерасход затрат, следовательно, увеличивать ее необходимо в первую очередь на этом звене.

Если бы было возможно увеличить пропускную способность d_1.11, то экономия от этого равнялась 75 ед. стоимости на каждую единицу груза.

Варианты заданий решения транспортной задачи в сетевой форме приведены в приложении.

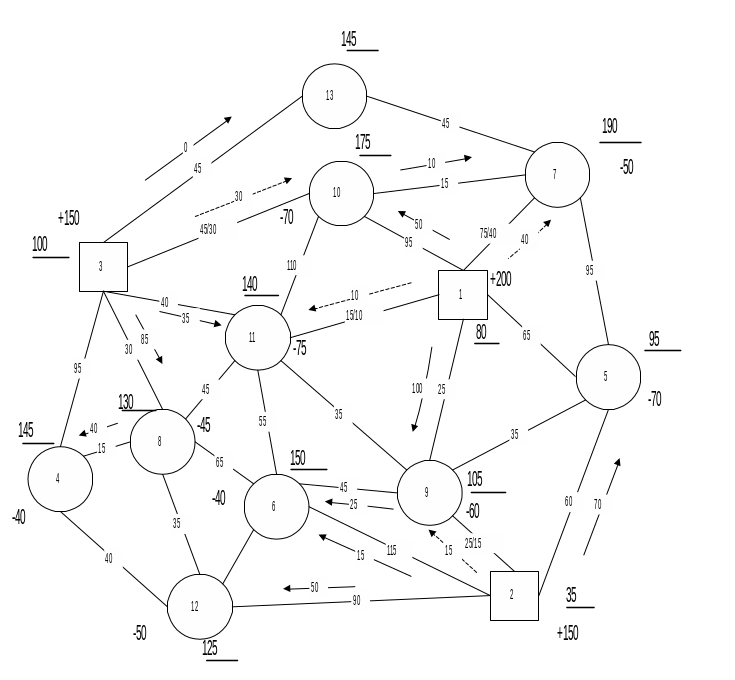Рис. 10