Преобразованная матрица показана в табл. 1.25
Таблица 1.25
III
IV |
5 |
10 |
5 |
(0) |
3 |
(0) |
7 |
8 |
(0) |
II
I |
4 |
(0) |
(0) |
- 2 |
6. Полученный план неоптимальный, поскольку С35 = -2 < 0. Строим цикл по выше приведенным правилам и производим корректировку плана перевозок. При этом клетка (1,5) разгрузилась, а клетка (3,5) нагрузилась. Новый план перевозок представлен в табл. 1.26.
Таблица 1.26
Станции отправления |
Запасы грузов |
Станции назначения |
||||
B1 |
B2 |
B3 |
B4 |
B5 |
||
130 |
220 |
60 |
70 |
80 |
||
A1 |
120 |
|
|
|
|
|
A2 |
280 |
|
|
|
|
|
A3 |
160 |
|
|
|
|
|
7. Полученный план перевозок проверим на отрицательность по вышеприведенной методике. Матрица стоимостей для нового приближения приведена в табл. 1.27.
0
- 2
- 2
(1) |
7 |
9 |
5 |
0 |
4 |
(2) |
6 |
8 |
(0) |
- 1 0
1 0 2 |
8 |
(1) |
(2) |
(0) |
Подсчитаем потенциалы:
1
+ U1
+ V1
= 0;
2 + U2 + V2 = 0;
0 + U2 + V5 = 0;
3 + U3 + V1 = 0; (1.44)
1 + U3 + V3 = 0;
2 + U3 + V4 = 0;
0 + U3 + V5 = 0.
Полагаем U1 = 0 и из полученной системы (1.44) находим :
V1 = - 1; V2 = 0; U2= - 2; V3 = 1; V4 = 0; V5 = 2.
Преобразованная матрица стоимостей приведена в табл. 1.28.
Таблица 1.28
0 |
7 |
10 |
5 |
2 |
1 |
0 |
5 |
6 |
0 |
0 |
6 |
0 |
0 |
0 |
Анализ табл. 1.28 показывает, что план перевозок является оптимальным и ТЗ имеет следующий оптимальный план :
X
=
.
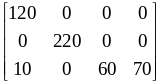При этом плане остаются неиспользованными 60 усл. ед. щебня во втором карьере и 20 усл. ед. в третьем карьере. Общая стоимость перевозок составляет:
F = 1·120 + 3·10 + 2·220 + 1·60 + 2·70 = 790.
При первоначальном плане перевозок транспортные издержки составляют: F = 1·40 + 4·60 + 2·220 + 3·30 + 1·60 + 2·70 = 1010.
Оптимальный план перевозок на 220 ед. дешевле.
Пример. Составить оптимальный план перевозок для следующей ТЗ (табл. 1.29).
Решение.
1. Проверим баланс наличия и потребления:
=
5 + 10 + 6 + 4 = 25;
=
7 + 3 + 7 + 8 = 25;
= .
Задача сбалансированная.
Таблица 1.29
Станции отправления |
Запасы грузов |
Станции назначения |
|||
B1 |
B2 |
B3 |
B4 |
||
7 |
3 |
7 |
8 |
||
A1 |
5 |
|
|
|
1
|
A2 |
10 |
|
|
3 . |
|
A3 |
6 |
|
|
|
|
А4 |
4 |
|
|
|
|
Построенный цикл состоит из шести вершин и начинается от элемента с максимальной по модулю отрицательной величиной стоимости (клетка (2, 3)).
2. Методом двойного предпочтения определим предварительный план перевозок, отвечающий условиям (1.26) - (1.28).
Необходимое число перевозок r = m + n - 1 = 4 + 4 - 1 = 7.
Условия оптимального числа перевозок не выполняется, поэтому введем фиктивную перевозку xij = 0 . Она должна располагаться так, чтобы выполнялось условие (1.26). В табл. 1.29, в клетке (1, 2) квадратом отмечена фиктивная перевозка.
3. Из заданной таблицей ТЗ выписываем матрицу стоимости (табл. 1.30) и отмечаем те клетки, в которых есть перевозки.
0
0
0
1
|
2 |
4 |
(1) |
(2) |
4 |
3 |
(1) |
4 |
4 |
(6) |
5 |
5 |
(1) |
(5) |
3 |
3
-
2 - 2 6 - 1
Справа от матрицы стоимости записываем значение потенциалов Ui . Следуя вышеизложенному правилу, имеем:
2 + V2 + U1 = 0;
1 + V4 + U1 = 0;
2 + V1 + U2 = 0;
1 + V4 + U2 = 0; (1.45)
6 + V3 + U3 = 0;
1 + V2 + U4 = 0;
5 + V3 + U4 = 0.
Полагая U1 = 0, тогда из (1.45) находим:
V2 = - 2 ; V4 = - 1 ; V1 = - 2 ; V3 = 6; U2 = 0 ; U3 = 0 ; U4 = 1.
В табл. 1.31 показана преобразованная матрица стоимости.
Поскольку табл. 1.31 содержит Cij < 0 клетка (2, 3) предварительный план перевозок не является оптимальным. В этой ситуации необходима корректировка плана перевозок, по вышеизложенному алгоритму строим цикл (табл. 1.31)
Таблица 1.31
-
IV
V
10
- 2
(0)
I
VI
(0)2
- 3
(0)
2
2
(0)
4
II
III
4(0)
(0)
3
Минимальная по объему перевозка находится у вершины IV цикла, клетка (1, 2).
Эта фиктивная перевозка, ее объем равен нулю. Во всех остальных отмеченных клетках имеются действительные перевозки за исключением клетки (2, 3), куда по правилам следует передвинуть фиктивную перевозку. Все остальные перевозки останутся без изменений, так как их объем изменяется на фиктивную величину, т.е. на ноль.
В табл. 1.32 показана матрица стоимости нового плана перевозок.
Таблица 1.32
0
0
- 3
- 2 |
2 |
4 |
(1) |
(2) |
4 |
3 |
(1) |
4 |
4 |
(6) |
5 |
- 2 1
- 3 - 1 |
(1) |
(5) |
3 |
Подсчитаем потенциалы.
1 + V4 + U1 = 0 ;
2 + V1 + U2 = 0 ;
3 + V3 + U2 = 0 ;
1 + V4 + U2 = 0 ; (1.46)
6 + V3 + U3 = 0 ;
1 + V2 + U4 = 0 ;
5 + V3 + U4 = 0 .
Полагая U1 = 0, тогда из (1.46) находим:
V2 = 1 ; V4 = - 1 ; V1 = - 2 ; V3 = - 3; U2 = 0 ; U3 = - 3 ; U4 = - 2.
В табл. 1.33 показана преобразованная матрица тарифов.
Наличие отрицательного элемента, клетка (3, 1), в матрице дает основание утверждать, что новый план не является оптимальным, поэтому для перераспределения грузопотока строим цикл (табл. 1.33).
Таблица 1.33
-
1
3
1
(0)
II
III
(0)5
0
(0)
I
IV
-12
(0)
1
1
(0)
(0)
0
По вышеизложенному алгоритму, перераспределяем объемы перевозок (табл. 1.34).
Таблица 1.34
-
7
3
7
8
5
10
6
4
Проверим полученный план перевозок на оптимальность. Для этого выпишем матрицу тарифов (табл. 1.35) и отметим те клетки, в которых есть перевозки.
Таблица 1.35
-
0
0
- 2
- 2
32
4
(1)
(2)
4
(3)
(1)
(4)
4
6
5
5
(1)
(5)
3
-
2 1
-3 -1
Найдем потенциалы Ui и Vj .
1 + V4 + U1 = 0;
2 + V1 + U2 = 0;
5 + V3 + U2 = 0;
1 + V4 + U2 = 0; (1.47)
4 + V1 + U3 = 0;
1 + V2 + U4 = 0;
5 + V3 + U4 = 0.
Пусть U1 = 0. Тогда из (1.47) находим:
V1 = - 2; V2 = 1 ; V3 = - 3; V4 = - 1;U2 = 0 ; U3 = - 2 ; U4 = - 2.
Преобразованная матрица тарифов показана в табл. 1.36.
Таблица 1.36
-
1
3
1
0
0
5
0
0
0
3
1
2
1
0
0
0
Поскольку в табл. 1.36 нет отрицательных элементов, то полученный план перевозок оптимальный.
Для того чтобы окончательно убедиться в оптимальности плана перевозок, следует сравнить суммарные стоимости перевозок предварительного и оптимального планов, пользуясь целевой функцией F.
Общая стоимость перевозок по предварительному плану составит (табл. 1.29):
F'
=
= 5 + 2 ·7
+3 + 6 ·6
+ 3 + 5 = 66.
Для оптимального плана (табл. 1.34):
Fопт
=
= 5 + 2 +3 ·6
+ 3 + 4 ·6
+ 5+3 = 60.
План в табл. 1.34 на шесть единиц дешевле предварительного плана (табл. 1.29).