5 Адиабатный процесс. Уравнение Пуассона. Первое начала термодинамики применительно к адиабатическому процессу.

А) Адиабати́ческий, или адиаба́тный проце́сс (от др.-греч. ἀδιάβατος — «непроходимый») — термодинамический процесс в макроскопической системе, при котором система не обменивается тепловой энергией с окружающим пространством .  Серьёзное исследование адиабатических процессов началось в XVIII веке^[1].

Адиабатический процесс является частным случаем политропного процесса, так как при нём теплоёмкость газа равна нулю и, следовательно, постоянна^[2]. Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётся равновесной (например, изменение состояния происходит достаточно медленно) и изменения энтропии не происходит. Некоторые авторы (в частности, Л. Д. Ландау) называли адиабатическими только квазистатические адиабатические процессы^[3].

Адиабатический процесс для идеального газа описывается уравнением Пуассона.  Линия, изображающая адиабатный процесс на термодинамической диаграмме, называется адиабатой. Адиабатическими можно считать процессы в целом ряде явлений природы. Так же такие процессы получили ряд применений в технике.

Б) Уравне́ние Пуассо́на — эллиптическое дифференциальное уравнение в частных производных, которое, среди прочего, описывает

• электростатическое поле,

• стационарное поле температуры,

• поле давления,

• поле потенциала скорости в гидродинамике.

Оно названо в честь знаменитого французского физика и математика Симеона Дени Пуассона.

Это уравнение имеет вид: 

где   — оператор Лапласа или лапласиан, а   — вещественная или комплексная функция на некотором многообразии.

В трёхмерной декартовой системе координат уравнение принимает форму:

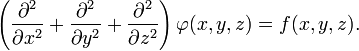
В декартовой системе координат оператор Лапласа записывается в форме   и уравнение Пуассона принимает вид:

Если f стремится к нулю, то уравнение Пуассона превращается в уравнение Лапласа (уравнение Лапласа — частный случай уравнения Пуассона):

Уравнение Пуассона может быть решено с использованием функции Грина; см., например, статью экранированное уравнение Пуассона. Есть различные методы для получения численных решений. Например, используется итерационный алгоритм — «релаксационный метод».

В) см в тетр.

6 Второе начало термодинамики, его содержание. Принцип начало работы тепловой машины. Цикл Карно.

А) Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.

Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая, что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не может равняться абсолютному нулю.

Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения.

]Формулировки

Существуют несколько эквивалентных формулировок второго начала термодинамики:

• Постулат Клаузиуса: «Невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему»^[1] (такой процесс называется процессом Клаузиуса).

• Постулат Томсона (Кельвина): «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара» (такой процесс называется процессом Томсона).

Эквивалентность этих формулировок легко показать. В самом деле, допустим, что постулат Клаузиуса неверен, то есть существует процесс, единственным результатом которого была бы передача тепла от более холодного тела к более горячему. Тогда возьмем два тела с различной температурой (нагреватель и холодильник) и проведем несколько циклов тепловой машины, забрав тепло   у нагревателя, отдав   холодильнику и совершив при этом работу  . После этого воспользуемся процессом Клаузиуса и вернем тепло   от холодильника нагревателю. В результате получается, что мы совершили работу только за счет отъёма теплоты от нагревателя, то есть постулат Томсона тоже неверен.

С другой стороны, предположим, что неверен постулат Томсона. Тогда можно отнять часть тепла у более холодного тела и превратить в механическую работу. Эту работу можно превратить в тепло, например, с помощью трения, нагрев более горячее тело. Значит, из неверности постулата Томсона следует неверность постулата Клаузиуса.

Таким образом, постулаты Клаузиуса и Томсона эквивалентны.

Другая формулировка второго начала термодинамики основывается на понятии энтропии:

• «Энтропия изолированной системы не может уменьшаться» (закон неубывания энтропии).

Такая формулировка основывается на представлении об энтропии как о функции состояния системы, что также должно быть постулировано.

Второе начало термодинамики в аксиоматической формулировке Рудольфа Юлиуса Клаузиуса (R. J. Clausius, 1865) имеет следующий вид^[2]:

Для любой квазиравновесной термодинамической системы существует однозначная функция термодинамического состояния  , называемая энтропией, такая, что ее полный дифференциал  .

В состоянии с максимальной энтропией макроскопические необратимые процессы (а процесс передачи тепла всегда является необратимым из-за постулата Клаузиуса) невозможны.

Б) Тепловая машина.

Устройство, преобразующее энергию теплового движения в механическую энергию, называется тепловой машиной. Различают циклические и нециклические тепловые машины.