1 Термодинамический и статический методы исследования. Понятие о равновесном процессе. Давление и температура идеального газа. Уравнение состояния идеального газа.

А) Молекулярная физика и термодинамика — разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержащихся в телах атомов и молекул. Для исследования этих процессов применяют два качественно различных и взаимно допол­няющих друг друга метода: статистический (молекулярно-кинетический) и термодинами­ческий. Первый лежит в основе молекулярной физики, второй — термодинамики.

Молекулярная физика — раздел физики, изучающий строение и свойства вещества исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в непрерывном хаотическом движении.

Идея об атомном строении вещества высказана древнегреческим философом Демо­критом (460—370 до н. э.). Атомистика возрождается вновь лишь в XVII в. и развива­ется в работах М. В. Ломоносова, взгляды которого на строение вещества и тепловые явления были близки к современным. Строгое развитие молекулярной теории относит­ся к середине XIX в. и связано с работами немецкого физика Р. Клаузиуса (1822—1888), Дж. Максвелла и Л. Больцмана.

Процессы, изучаемые молекулярной физикой, являются результатом совокупного действия огромного числа молекул. Законы поведения огромного числа молекул, являясь статистическими закономерностями, изучаются с помощью статистического метода. Этот метод основан на том, что свойства макроскопической системы в конеч­ном счете определяются свойствами частиц системы, особенностями их движения и усредненными значениями динамических характеристик этих частиц (скорости, энер­гии и т. д.). Например, температура тела определяется скоростью хаотического движе­ния его молекул, но так как в любой момент времени разные молекулы имеют различные скорости, то она может быть выражена только через среднее значение скорости движения молекул. Нельзя говорить о температуре одной молекулы. Таким образом, макроскопические характеристики тел имеют физический смысл лишь в слу­чае большого числа молекул.

Термодинамика — раздел физики, изучающий общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехо­да между этими состояниями. Термодинамика не рассматривает микропроцессы, кото­рые лежат в основе этих превращений. Этим термодинамический метод отличается от статистического. Термодинамика базируется на двух началах — фундаментальных за­конах, установленных в результате обобщения опытных данных.

Область применения термодинамики значительно шире, чем молекулярно-кинетической теории, ибо нет таких областей физики и химии, в которых нельзя было бы пользоваться термодинамическим методом. Однако, с другой стороны, термодинами­ческий метод несколько ограничен: термодинамика ничего не говорит о микроскопи­ческом строении вещества, о механизме явлений, а лишь устанавливает связи между макроскопическими свойствами вещества. Молекулярно-кинетическая теория и термо­динамика взаимно дополняют друг друга, образуя единое целое, но отличаясь различ­ными методами исследования.

Б) РАВНОВЕСНЫЙ ПРОЦЕСС

(квазистатический процесс) в термодинамике- процесс перехода термодинамич. системы из одного равновесного состояния в другое, столь медленный, что все промежуточные состоянии можно рассматривать как равновесные, т. е. характеризующиеся очень медленным (в пределе - бесконечно медленным) изменением термодинамич. параметров состояния. Р. п.- одно из осн. понятий термодинамики равновесных процессов. Всякий Р. п. является обратимым процессом, и наоборот, любой обратимый процесс является равновесным.

В) Чем больше температура, тем больше объем , или давление.

Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.

Г) Используя зависимость давления идеального газа от его температуры и концентрации молекул

p = nkT ,

можно найти связь между основными макроскопическими параметрами газа — объемом V, его давлением p и температуройT.    Концентрация n молекул газа равна

 , (26.1)

где N — число молекул газа в сосуде объемом V. Число N можно выразить как произведение количества вещества   на постоянную Авогадро N_A:

 . (26.2)

Из выражений (25.9), (26.1) и (26.2) получаем

 . (26.3)

Произведение постоянной Авогадро N_A на постоянную Больцмана k называется молярной газовой постоянной R. Молярная газовая постоянная равна

 . (26.4)

Используя молярную газовую постоянную, выражение (26.3) преобразуем в уравнение

 . (26.5)

Количество вещества   можно найти, зная массу вещества m и его молярную массу M:

 , (26.6)

поэтому уравнение (26.5) можно записать в такой форме:

. (26.7)

Это уравнение называется уравнением состояния идеального газа.    Уравнение, устанавливающее связь между давлением, объемом и температурой газов, было получено французским физиком Бенуа Клапейроном (1799—1864). В форме (26.7) его впервые применил великий русский ученый Дмитрий Иванович Менделеев (1834—1907), поэтому уравнение состояния газа называется уравнением Менделеева — Клапейрона.    Для исследования связи между объемом, давлением и температурой газа можно использовать герметичный сосуд, объем которого может изменяться. Внешний вид такого прибора — сильфона — представлен на рисунке 87.

Изопроцессы в газах. Уравнение (26.7) показывает, что возможно одновременное изменение пяти параметров, характеризующих состояние идеального газа. Однако многие процессы в газах, происходящие в природе и осуществляемые в технике, можно рассматривать приближенно как процессы, в которых изменяются лишь два параметра из пяти. Особую роль в физике и технике играют три процесса — изотермический, изохорный и изобарный. Рассмотрим эти процессы.

Изотермический процесс. Изотермическим процессом называется процесс, протекающий при постоянной температуре T. Из уравнения состояния идеального газа (26.7) следует, что при постоянной температуре T и неизменных значениях массы газа и его молярной массы M произведение давления p газа на его объем V должно оставаться постоянным:

 . (26.8)

Изотермический процесс можно осуществить, например, путем изменения объема газа при постоянной температуре.    График изотермического процесса называется изотермой. Изотерма, изображенная в прямоугольной системе координат, по оси ординат которой отсчитывается давление газа, а по оси абсцисс — его объем, является гиперболой (рис. 88).

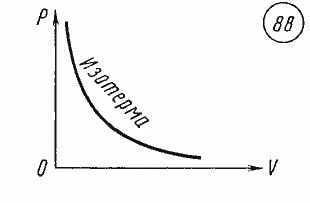
Уравнение (26.8), устанавливающее связь между давлением и объемом газа при постоянной температуре, было получено из эксперимента до создания молекулярно-кинетической теории газов в 1662 г. английским физиком Робертем Бойлем (1627 — 1691) и в 1676 г. французским физиком Эдмом Мариоттом (1620—1684). Поэтому это уравнение называют законом Бойля — Мариотта.

Изохорный процесс. Изохорным процессом называется процесс, протекающий при неизменном объеме V и условии m = const и M = const.    При этих условиях из уравнения состояния идеального газа (26.7) для двух значений температуры T₀ и T следует

    и     ,

или

,    

   Если T₀ выбрать равным 273 К (0 °С), то  . Обозначив  , получим уравнение для изохорного процесса

 , (26.9)

где p — давление газа при абсолютной температуре T, p₀ — давление газа при температуре 0 °С,  — температурный коэффициент давления газа, равный  .

   График уравнения изохорного процесса называется изохорой. Изохора, изображенная в прямоугольной системе координат, по оси ординат которой отсчитывается давление газа, а по оси абсцисс — его абсолютная температура, является прямой, проходящей через начало координат (рис. 89).

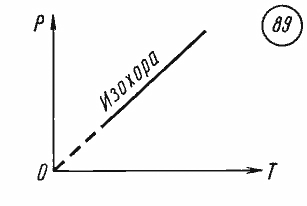
Экспериментальным путем зависимость давления газа от температуры исследовал французский физик Жак Шарль (1746—1823) в 1787 г. Поэтому уравнение (26.9) называется законом Шарля.

   Изохорный процесс можно осуществить, например, нагреванием воздуха при постоянном объеме.

Изобарный процесс. Изобарным процессом называется процесс, протекающий при неизменном давлении p и условии m = const и M = const.

   Таким же способом, как это было сделано для изохорного процесса, можно получить для изобарного процесса уравнение

 , (26.10)

где V — объем газа при абсолютной температуре T, V₀ — объем газа при температуре 0 °С; коэффициент  , равный  , называется температурным коэффициентом объемного расширения газов.

   График уравнения изобарного процесса называется изобарой. Изобара, изображенная в прямоугольной системе координат, по оси ординат которой отсчитывается объем газа, а по оси абсцисс — его абсолютная температура, является прямой, проходящей через начало координат (рис. 90).

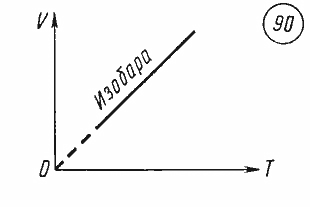
Экспериментальное исследование зависимости объема газа от температуры провел в 1802 г. французский физик Жозеф Гей-Люссак (1778—1850). Поэтому уравнение (26.10) называется законом Гей-Люссака.

   Изобарный процесс происходит, например, при нагревании или охлаждении воздуха в стеклянной колбе, соединенной со стеклянной трубкой, отверстие в которой закрыто небольшим столбом жидкости (рис. 91).