24.1 Дробный факторный эксперимент.

Свойство ПФЭ – большое число опытов. Задача – сокращение числа опытов за счет информации которая не существенна при построении линейных моделей.(при этом матрица планирования сохраняет оптимальные свойства ).

 24.4 Поверка свойств матрицы планов.

Заданы две матрицы, д/б определены условия (выполнение условий для этих матриц )

Матрица (таблица) плана 1:

№	Z0	Z1	Z2	Z3	Y
1 2 3 4	+ + + +	- + - +	- + + -	+ - - +	y1 y2 y3 y4

Столбец Z3 содержит произвольные (не связанные с Z1 и Z2) комбинации значений уравнений.(использование данного плана приведет к потере данных о процессе.)

1. Cв-во суммирования элем-ов

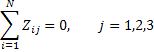
2. Св-во ортогональности:

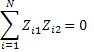
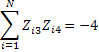
3. Т.о. св-во ортогональности матрицы плана не выполняется =›ошибочное построение вектора Z3

(обратны знаку Z2, т.е. Z3=-Z2)

Матрица(таблица) плана 2:

№	Z0	Z1	Z2	Z3	Y
1 2 3 4	+ + + +	- + - +	- + + -	+ + - -	y1 y2 y3 y4

24.3 Переход от полного факторного эксперимента к дробному.

Модель для двух факторов:

Y=b₀+b₁x₁+b₂x₂+b₁₂x₁x₂ (1)

Модель для трех факторов:

Y=b₀+b₁x₁+b₂x₂+b₃x₃ (2)

Y=β₀+β₁x₁+β₂x₂+β₃x₃+β₁x₁x₃+β₂₃x₂x₃ (3)

^{Исполнительная табл-а ПФЭ 2}2

№	Z0	Z1	Z2	Z3	Y
1 2 3 4	+ + + +	- + - +	- - + +	+ - - +	y1 y2 y3 y4

Данная матрица планирования позволяет определить коэф-ты b1 b2 b12 для линейной модели 3 – коэффициента: b0 b1 b2 (т.е. эффекты взаимодействия факторов учитыватся не будут). В предположении что b12 -› 0

Вектор столбец Z1Z2 используется для планирования эксперимента с новым фактором Z3. Предполагается что на основе данного дробного эксперимента определяются смешанные оценки коэффициентов в выражении (3)

Т.о.:

1. Вместо b1 ,в выраж-и (2) определяется β2+β23 в (3)

2. Вместо b2 опред-я β2+β13 в (3)

3. Вместо b3 (аналог β3 в(3)) опр-я β3+β12

В силу того что при построении линейной модели все парные взаимодействия незначимы, то

b1≈β1 , b2≈β2, b3≈β3

т.о. правило уменьшения числа опытов опред в след виде:

для сокращения числа опытов нужно новому фактору присвоить вектор столбец матрицы, соответствующий взаимодействию, которым можно принебречь. Значения нового фактора определяются знаками в столбце взаимодействия. Тогда вместо восьми опытов для 3-х факторов м\б 4 опыта . при этом матрица планирования должна удовлетворять свойствам суммирования элементов, условию нормировки и условию ортогональности.

-условия суммирования элементов

-условия нормировки:

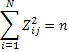
-условия ортогональности:

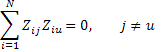
YFRJYTWNJ <KZ!!!!!!!!!!!!!