
- •8Модели дискретных детерминированных систем. Общие понятия. Операторное представление моделей дискретных систем.
- •11. Конечно-автоматные модели дискретных систем. Вводные понятия. Функционирование конечного автомата. Примеры.
- •14 Алгоритмы формирования псевдослучайных чисел на эвм.
- •17).Понятие модельного времени при имитационном моделировании. Способы формирования модельного времени. Принцип ∆t и ∆z.
- •20. Планирование имитационных экспериментов. Определение оценок параметров регрессионной модели. Матричные и скалярные выражения для определения параметров.
- •21.Построение оптимальных планов регрессионных экспериментов. Математическая формулировка задачи.
- •23.1Способы построения матрицы плана.
- •24.1 Дробный факторный эксперимент.
20. Планирование имитационных экспериментов. Определение оценок параметров регрессионной модели. Матричные и скалярные выражения для определения параметров.
Определение
метода идентификации значений параметров
![]() поясним на примере. В качестве входных
данных модели используются 3 фазовые
координаты
поясним на примере. В качестве входных
данных модели используются 3 фазовые
координаты ![]() ,
,![]() ,
,
![]() .
Реализуется 3 опыта, в каждом из которых
задаются определенные значения входных
параметров (фазовых координат
.
Реализуется 3 опыта, в каждом из которых
задаются определенные значения входных
параметров (фазовых координат ![]() ,
,
![]() ,
,
![]() ).
Тогда через
).
Тогда через ![]() может
быть обозначено значение j-ой
переменной (j=
может
быть обозначено значение j-ой
переменной (j=![]() )
в i-ом
опыте (i=
).
Выражение (в упрощенной форме) для
регрессионной модели, построенной по
результатам k-го
эксперимента, имеет вид:
)
в i-ом
опыте (i=
).
Выражение (в упрощенной форме) для
регрессионной модели, построенной по
результатам k-го
эксперимента, имеет вид:
![]()
Для трех опытов выход системы связан со значениями входных параметров :
![]()
![]()
![]() , т.о.
, т.о. ![]() -
первая точка плана эксперимента,
-
первая точка плана эксперимента,![]() -
вторая точка плана эксперимента,
-
вторая точка плана эксперимента, ![]() -
третья точка плана эксперимента.
Выражение в матричной форме для
определения значений (оценок) параметров
имеют вид:
-
третья точка плана эксперимента.
Выражение в матричной форме для
определения значений (оценок) параметров
имеют вид:
![]() или
или
![]() (1), где Y-
вектор наблюдений выхода в точках плана,
Z(F)-
матрица значений функций
(1), где Y-
вектор наблюдений выхода в точках плана,
Z(F)-
матрица значений функций ![]() в точках плана (т.е.
в точках плана (т.е. ![]() )
)
21.Построение оптимальных планов регрессионных экспериментов. Математическая формулировка задачи.
Выражение (1) позволяет получить оценки неизвестных параметров регрессионной модели, т.к. эксперимент- активный, то возможен выбор значений контролируемых переменных, т.е. возможно задание различных векторов Z входных данных- комбинаций значений фазовых координат.
Точность
оценивания параметров
(вектор ![]() )
зависит от информационной матрицы М,
которая определяется множеством точек
{
)
зависит от информационной матрицы М,
которая определяется множеством точек
{![]() }
плана эксперимента (
}
плана эксперимента (![]() -
одна комбинация входных значений). Т.о.
набор точек {
}-
план эксперимента.
-
одна комбинация входных значений). Т.о.
набор точек {
}-
план эксперимента.
Дискретным планом эксперимента называют матрицу вида:
![]() (1), где
-
соответствующие комбинации исходных
данных,
(1), где
-
соответствующие комбинации исходных
данных, ![]() -
частота повторения i-го
набора входных данных при проведении
N
опытов. Т.о.
-
частота повторения i-го
набора входных данных при проведении
N
опытов. Т.о. ![]() ,
, ![]() ,
,
![]() ,
,
![]() -
число повторений комбинации
в N
опытах.
-
число повторений комбинации
в N
опытах.
Т.о.
всего n
комбинаций входных данных проводится
N
опытов, в N
опытах, каждая комбинация
исходных данных повторяется
-
раз (в результате определяется параметр
![]() -
частота повторения комбинации
).
-
частота повторения комбинации
).
Т.о. задача планирования эксперимента (регрессионного) сводится к определению параметров так, чтобы оценки были оптимальными в соответствии с заданным критерием.
23.1Способы построения матрицы плана.
Альтернативный способ построения матрицы плана(правила формирования матрицы):
1-ый столбец – знаки меняются поочередно;
2-ой столбец – знаки чередуются через 2;
3-ий столбец знаки чередуются через 4;
4-ый столбец -\\-через 8 и т.д.
Пример матрицы планирования (Zi(i=1,3)
№ |
Z1 |
Z2 |
X3 |
Y |
1 2 3 4 5 6 7 8 |
- + - + - + - + |
- - + + - - + + |
+ + + + - - - - |
y1 y2 y3 y4 y5 y6 y7 y8 |
23.2 Свойства матрицы плана эксперимента 2k
Алгебраическая сумма элементов вектор столбца равна числу опытов:
![]() , где j=(1,m)-вектор
, где j=(1,m)-вектор
Условие : сумма квадратов элементов каждого столбца равна числу ответов :
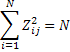
Свойства ортогональности матрицы планирования: сумма произведения элементов любых двух вектор-столбцов равна 0, т.е.:

23.3 Определение коэффициентов регрессионной модели по результатам ПФЭ (2k)
Модель Y=Ѳ0+Ѳ1X1+Ѳ2X2 (ПФЭ 2k). Цель- определить по результатам эксперимента значения неизвестных коэффициентов модели точность оценки коэффициентов Ѳj зависит от св-в выборки и нуждается в статистической проверке. Простейший способ вычисления параметров Ѳj:
![]() (1)
(1)
Где j=0,1,2,…k, zij- i-ый элемент j-го столбца плана ПФЭ. С учетом (1) определение Ѳ1 и Ѳ2 выполнено с. о.:
![]()
![]()
Т.о. расчет коэф-ов Ѳ1 и Ѳ2 выполняется на основе кодированных значений Zi соответствующих факторов (Ѳ2 – вектор-столбец Z2)
