14 Алгоритмы формирования псевдослучайных чисел на эвм.

Программнный датчик СВ-программа, служащая для имитации на ЭВМ реализаций базовой СВ. В общем виде функционирование датчика СВ описывается

формулой: (1)

где - выходная величина датчика в момент времени t (случайное число), - используемые при формировании предыдущие значения СВ.

Значение фиксируется заранее и называется стартовым числом (возможно случайным).Формула (1) рекуррентная, позволяет получить последовательность псевдослучайных чисел. Использован термин «псевдослучайные числа», такими могут быть:

1)числа получены по известному детерминированному закону;Методы построения програмнных датчиков СВ:

1.Мультипликативный конгруэнтный метод (метод вычетов).

Согласно этому методу псевдослучайная последовательность вычисляется по рекуррентным формулам :

где -параметры програмнного датчика(натуральные числа), - начальный элемент последовательности,М-сколь угодно большое число, -стартовое значение.Операция у=(z)mod M означает вычет числа z по модулю М: у= z-М[z/M], где [.]-операция целой части числа.

Параметры могут быть выбраны в соответствии со значениями в таблице.

q	M
32	=2147483648	+3=65539	65539

где q-разрядность ЭВМ.

1.Метод использующий линейные смешанные формулы:

Параметры датчика:р-порядок,

-стартовое значение

-множители,с-приращение,М-достаточно большое число.

1.Метод использующий линейные рекуррентные формулы: ,

где М- достаточно большое число(М=29)

-задаваемые значения.

17).Понятие модельного времени при имитационном моделировании. Способы формирования модельного времени. Принцип ∆t и ∆z.

Принцип Δt

1.Ось времени разбывается на равные временные интервалы (такты) длительностью Δt. МВ может принимать только дискретные значения, кратные Δt: Δt, 2Δt, 3Δt, … т.о. моделирующая программа формирует модельное время в соответствивии с формулой:

Реальный объект прогнозирования событияначинается Δt

Для управления модельным временем в программе создается переменная – счетчик модельного времени Т. который считает количество вынашенных тактов (в начале моделирования Т=0; затем Т=Т+1) При этом Т изменяется от 0 до Т max

Временные отметки (моменты времени моделирования) не привязаны к появлению реальных событий на объекте. Реальные события сдвигается к левой границе такта, в пределах которого оно поделено. Схема приязывания событий к началу тактов

Схема привязывания собития к началу тактов

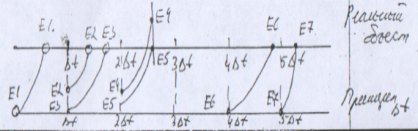
Принцип Δz

Особенность – прогнозирования момента времени наступления некоторого события в системе.

1.Перед началом моделирования счетчик модельного времени сбрасывается в 0 (t_m=0), задается начальное состояние системы (z₀)

2.Затем прогнозируется появление следующего события z₁ и определения момента времени t_m, для этого события

3.Текущему времени присваивается значение t_m1 (t_m =t_m1)

4.Имитируется реакция системы на событие Е1 (появление новых событий (события Е2 и t_m =t_m2))

5.Шкала модельного времени получается неравномерной

т. е. в методе Δz на основе текущего события прогнозируется следующее возможные (прогнозируется появление одного из слудеющих возможных событий)

схема моделирования (определение модельного времени)

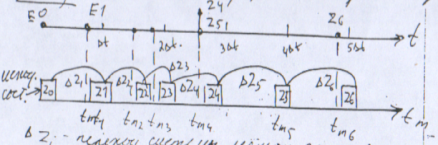
Δz- переход системы между состояниями