№1 Понятие системы и ее функционирования. Элементы системы ,связи между элементами, структура системы. Динамика системы.

Система есть совокупность взаимосвязанных элементов, объединенных в одно целое для достижения определенной цели.

Процесс функционирования системы во времени описывается операторными выражениями (где оператор- либо аналитическое выр-е (формула), либо некоторым алгоритмом или способом). Операторные выражения формируются для фазовых координат(вектора) и выхода системы.

Обобщенная форма операторных выражений. ,(1)

- способ отображения вх-х хар-к в некоторое состояние системы. -предполагается, что некоторое состояние является нулевым. - способ отображения вх-х параметров и соответствие системы в ее выход.

(1)-законы функционирования Системы.

Рассмотренный закон функционирования является математическим описанием поведения сложной системы во времени, а, следовательно, отражает его динамические свойства. Математические модели таких систем мы ранее называли динамическими моделями. Для статических моделей математическая запись лишается временного параметра и в векторной форме может быть записана в виде

№2 Понятие математической модели системы. Переменные ,характеризующие функционирование системы. Обобщенное операторное представление модели системы.

Логические схемы упрощающие рассуждения и логические построения или позволяющие проводить эксперименты, уточняющие природу явлений, наз. моделями.

Mатематическая модель системы - математическое описание, отражающее с требуемой точностью поведение реальной системы в реальных условиях.

математическая модель системы – это совокупность соотношений (формул, неравенств, уравнений, логических соотношений), определяющих характеристики состояний системы в зависимости от ее параметров, начальных условий, входных сигналов, включая случайные факторы, и времени.

Исходной информацией при построении математических моделей процессов функционирования систем служат данные о назначении и условиях работы исследуемой системы S. Эта информация определяет основную цель моделирования системы S и позволяет сформулировать требования к разрабатываемой математической модели совокупность входных воздействий на систему(вх-е с-ы; упр.-я)

,i = ; совокупность воздействий внешней среды l = ; -совокупность внутренних параметров системы k = ;-совокупность выходных характеристик системы j = .

В общем случае являются элементами непересекающихся подмножеств и содержат как детерминированные, так и стохастические составляющие.

При моделировании системы S входные воздействия, воздействия внешней среды Е и внутренние параметры системы являются независимыми (экзогенными) переменными, которые в векторной форме имеют соответственно вид

а выходные характеристики системы являются зависимыми (эндогенными) переменными и в векторной форме имеют вид

= {

Обозначения:

1) [t0; T]-временной интервал моделиров.-я системы; tЄ[t0;T] момент времени моделирования.

2) Q1,Q2,…Qm-характеристики системы, являющиеся сonst и неизменяющимися во вреьени.{Q1,Q2,…Qm}-множество значений параметров Є Q, где Q- множество значений параметров системы.

3) переменные, характеризующие функционирование системы.

А)Независимые переменные

-воздействие на систему(входные сигналы,управление.)

-воздействия внешней среды(Детерминированные или стахостические)

-переменные характеризующие состояние системы

Б)Зависимые переменные-это вых. Характеристики системы Y₁ Y₂…Y_P

№ 3 Классификация аналитических моделей систем.

Цель и задачи моделирования. Обобщение операторных выражений моделей систем в векторной форме (вектора входов, состояний и выходов).

Ответ.

. Компьютерная модель – это программная реализация математической модели, дополненная различными служебными программами (например, рисующими и изменяющими графические образы во времени). Компьютерная модель имеет две составляющие – программную и аппаратную. Программная составляющая так же является абстрактной знаковой моделью. Это лишь другая форма абстрактной модели, которая, однако, может интерпретироваться не только математиками и программистами, но и техническим устройством – процессором компьютера.

При аналитическом моделировании процессы функционирования элементов записываются в виде математических соотношений (алгебраических, интегральных, дифференциальных, логических и др.).

Для аналитического моделирования характерно то, что процессы функционирования элементов системы записываются в виде некоторых функциональных соотношений (алгебраических, интегродиференциальных, конечно-разностных и т.п.) или логических условий.

Аналитическое моделирование: описание S функциональными соотношениями (дифференциальные и интегральные уравнения, алгебраические уравнения) с последующей попыткой решить их аналитически или численными методами.

Аналитическая модель может быть исследовано методами:

а) аналитическим: получают в явном виде зависимости для искомых характеристик;

б) численными: получают числовые результаты при конкретных начальных данных;

в) качественными: не имея в явном виде решения можно найти свойства решения.

При усложнении систем применение аналитических методов вызывает затруднения, приходится идти на упрощение модели.

Численный метод позволяет использовать более широкий класс систем, но решения носят при этом частный характер.

Классификация.

Численное моделирование использует методы вычислительной математики.

Статистическое моделирование использует обработку данных о системе с целью получения статистических характеристик системы.

Имитационное моделирование воспроизводит на ЭВМ (имитирует) процесс функционирования исследуемой системы, соблюдая логическую и временную последовательность протекания процессов, что позволяет узнать данные о состоянии системы или отдельных ее элементов в определенные моменты времени.

Применение математического моделирования позволяет исследовать объекты, реальные эксперименты над которыми затруднены или невозможны.

Цели моделирования:

1) оценка – оценить действительные характеристики проектируемой или существующей системы, определить насколько система предлагаемой структуры будут соответствовать предъявляемым требованиям.

2) сравнение – произвести сравнение конкурирующих систем одного функционального назначения или сопоставить несколько вариантов построения одной и той же системы.

3) прогноз – оценить поведение системы при некотором предполагаемом сочетании рабочих условий.

4) анализ чувствительности – выявить из большого числа факторов, действующих на систему тем, которое в большей степени влияют на ее поведение и определяют ее показатели эффективности.

5) оптимизация – найти или установить такое сочетание действующих факторов и их величин, которое обеспечивает наилучшие показатели эффективности системы в целом.

1-4 задачи анализа, 5 - задача синтеза.

Компьютерная модель – это программная реализация математической модели, дополненная различными служебными программами (например, рисующими и изменяющими графические образы во времени). Компьютерная модель имеет две составляющие – программную и аппаратную. Программная составляющая так же является абстрактной знаковой моделью. Это лишь другая форма абстрактной модели, которая, однако, может интерпретироваться не только математиками и программистами, но и техническим устройством – процессором компьютера.

№4 Модели детерминированных систем. Системы с непрерывным временем. Свойства непрерывности отображений F(·) и G(·). Обоснование модели непрерывной детерминированной системы (уравнения состояния).

Детерминирован­ное моделирование отображает процессы, в которых предполагается отсутствие всяких случайных воздействий; стохастическое моделирование отображает вероят­ностные процессы и события. В этом случае анализируется ряд реализаций случайного процесса и оцениваются средние характе­ристики, т. е. набор однородных реализаций.Непрерывно детерминированные модели (Д - схемы).Рассмотрим особенности непрерывно детерминированного подхода на примере, используя в качестве ММ дифференциальные уравнения.

Дифференциальными уравнениями называются такие уравнения, в которых неизвестными будут функции одной переменной или нескольких переменных, причём в уравнение входят не только их функции но их производные различных порядков.

Пусть имеем уравнение:

- уравнение «вход-выход» (1)

Решение уравнения (1) зависит от K(t), от начальных условий . Эти координаты определяют начальное состояние системы.

Левую часть нужно привести к уравнению 1-го порядка.

- переменные состояния

(2)

(2) – уравнение в нормальной форме Коши, которое можно записать в матричной форме

(3) – уравнение в пространстве состояний

z – в-р столбец переменного состояния

, необходимое условие

- матрица коэффициентов координат состояния

- матрица коэффициентов входных воздействий

- некоторые числовые матрицы

Сопоставляя (2) и (3) получим числовые матрицы

;

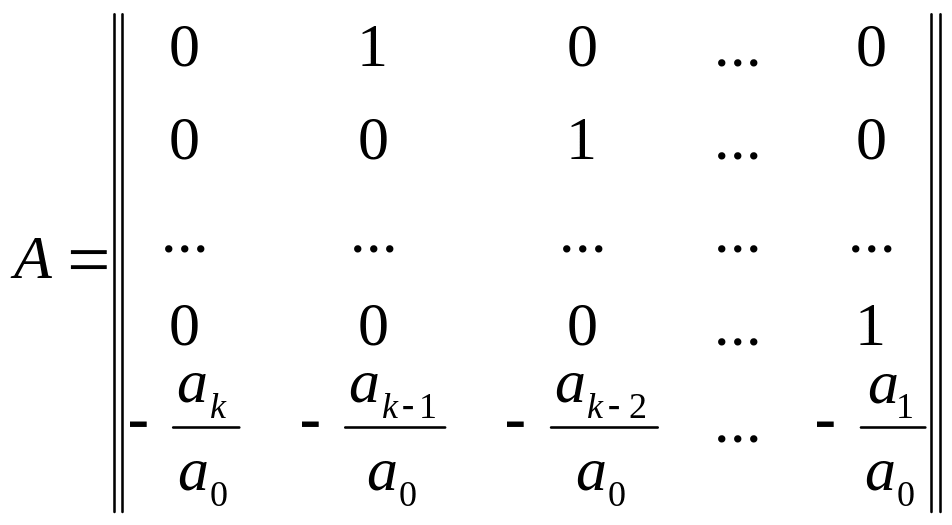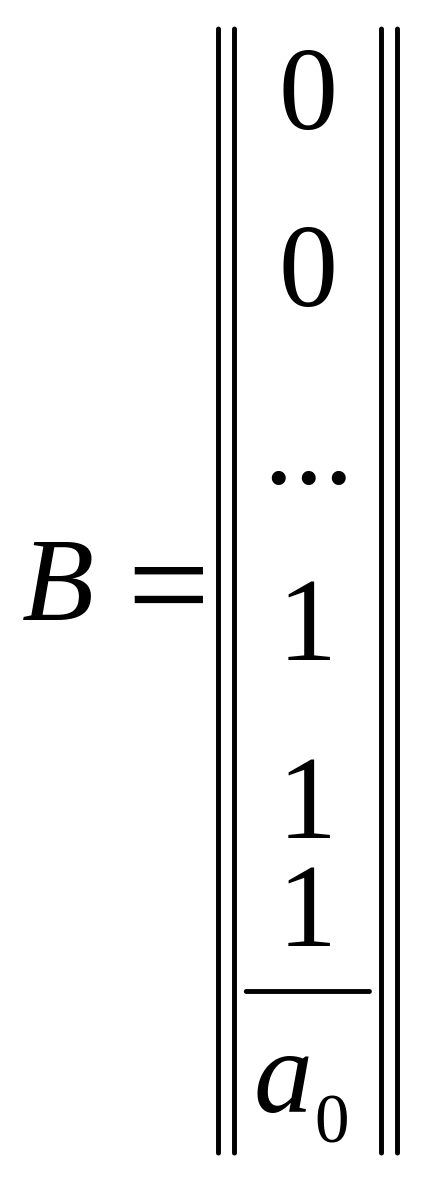
, D = 0 (4)

В общем случае, когда передаточная функция системы

имеет полиноминальную функцию

, где , то матрица А определяется выражением (4), а В имеет вид

7Формирование модели линейной детерминированной непрерывной системы (уравнения состояния).

К непрерывно-детерминированным моделям относятся модели, описываемые системами обыкновенных дифференциальных уравнений или уравнений в частных производных. В качестве независимой переменной, от которой зависят неизвестные искомые функции, обычно служит время. Тогда вектор-функция искомых переменных будет непрерывной. Математические схемы такого вида отражают динамику изучаемой системы и поэтому называются D-схемами (англ. dynamic).Рассмотрим особенности непрерывно детерминированного подхода на примере, используя в качестве ММ дифференциальные уравнения-такие уравнения, в которых неизвестными будут функции одной переменной или нескольких переменных, причём в уравнение входят не только их функции но их производные различных порядков.Если неизвестные - функции многих переменных, то уравнения называются — уравнения в частных производных. Если неизвестные функции одной независимой переменной, то имеют место обыкновенные дифференциальные уравнения.

Математическое соотношение для детерминированных систем в общем виде:

(7).Диф. уравнения, Д - схемы являются математическим аппаратом теории систем автоматического регулирования, управления.

При проектировании и эксплуатации систем САУ необходимо выбрать такие параметры системы, которые бы обеспечивали требуемую точность управления.

Следует отметить, что часто используемые в САУ системы диф. уравнений определяются путём линеаризацией управления объекта (системы), более сложного вида, имеющего нелинейности:

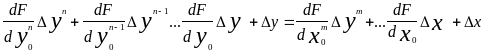
8Модели дискретных детерминированных систем. Общие понятия. Операторное представление моделей дискретных систем.

К дискретно-детерминированным моделям относятся так называемые конечные автоматы. Автомат можно представить как некоторое устройство, на которое подаются входные сигналы и снимаются выходные и которое может иметь некоторые внутренние состояния. У конечного автомата множество входных сигналов и внутренних состояний является конечным множеством. Название F-схема происходит от английских слов finite automata.Дискретно – детерминированные модели (F-схемы).ДДМ являются предметом рассмотрения теории автоматов (ТА). ТА - раздел теоретической кибернетики, изучающей устройства, перерабатывающие дискретную информацию и меняющего свои внутренние состояния лишь в допустимые моменты времени.Конечный автомат имеет множество внутренних состояний и входных сигналов, являющихся конечными множествами. Автомат задаётся F- схемой: F=<z,x,y,,,z₀>,(1) где z,x,y - соответственно конечные множества входных, выходных сигналов (алфавитов) и конечное множество внутренних состояний (алфавита). z₀Z - начальное состояние; (z,x) - функция переходов; (z,x) - функция выхода. Автомат функционирует в дискретном автоматном времени, моментами которого являются такты, т.е. примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного, выходного сигнала и внутреннего состояния. Абстрактный автомат имеет один входной и один выходной каналы.В момент t, будучи в состоянии z(t), автомат способен воспринять сигнал x(t) и выдать сигнал y(t)=[z(t),x(t)], переходя в состояние z(t+1)=[z(t),z(t)], z(t)Z; y(t)Y; x(t)X. Абстрактный КА в начальном состоянии z₀ принимая сигналы x(0), x(1), x(2)выдаёт сигналы y(0), y(1), y(2)(выходное слово).Существуют F- автомат 1-ого рода (Миля), функционирующий по схеме:z(t+1)= [z(t),z(t)], t=0,1,2..(1)y(t)=[z(t),x(t)], t=0,1,2…(2)F-автомат 2-ого рода:z(t+1)= [z(t),z(t)], t=0,1,2…(3)y(t)=[z(t),x(t-1)], t=1,2,3…(4)Автомат 2-ого рода, для которого y(t)=[z(t)], t=0,1,2,…(5)т.е. функция выходов не зависит от входной переменной x(t), называется автоматом Мура.

Т.о. уравнения 1-5 полностью задающие F- автомат, являются частным случаем уравнения (6)где - вектор состояния, - вектор независимых входных переменных, - вектор воздействий внешней среды, - вектор собственных внутренних параметров системы, - вектор начального состояния, t - время; и уравнение , (7)когда система S - денорминированная и на её вход поступает дискретный сигнал x.По числу состояний конечные автоматы бывают с памятью и без памяти. Автоматы с памятью имеют более одного состояния, а автоматы без памяти (комбинационные или логические схемы) обладают лишь одним состоянием. При этом согласно (2), работа комбинационной схемы заключается в том, что она ставит в соответствие каждому входному сигналу x(t) определённый выходной сигнал y(t), т.е. реализует логическую функцию вида:y(t)=[x(t)], t=0,1,2,…Эта функция называется булевой, если алфавиты X и Y, которым принадлежат значения сигналов x и y состоят из 2-х букв.По характеру отсчёта времени (дискретному) F- автоматы делятся на синхронные и асинхронные. В синхронных автоматах моменты времени, в которые автомат "считывает" входные сигналы, определяются принудительно синхронизирующими сигналами. Реакция автомата на каждое значение входного сигнала заканчивается за один такт синхронизации. Асинхронный F- автомат считывает входной сигнал непрерывно и поэтому, реагируя на достаточно длинный водной сигнал постоянной величины x, он может, как это следует из 1-5, несколько раз изменить своё состояние, выдавая соответствующее число выходных сигналов, пока не перейдёт в устойчивое.Для задания F- автомата необходимо описать все элементы множества F=<z,x,y,,,z₀>, т.е. входной, внутренний и выходной алфавиты, а также функции переходов и выходов. Для задания работы F- автоматов наиболее часто используются табличный, графический и матричный способ.В табличном способе задания используется таблицы переходов и выходов, строки которых соответствуют входным сигналам автомата, а столбцы - его состояниям. При этом обычно 1-ый столбец слева соответствует начальному состоянию z­₀. На пересечении i-ой строки и j-ого столбца таблицы переходов помещается соответствующее значение (z_k,x_i) функции переходов, а в таблице выходов - (z_k, x_i) функции выходов. Для F- автомата Мура обе таблицы можно совместить, получив т.н. отмеченную таблицу переходов, в которой над каждым состоянием z_k автомата, обозначающим столбец таблицы, стоит соответствующий этому состоянию, согласно (5), выходной сигнал (z_i).При другом способе задания конечного автомата используется понятие направленного графа. Граф автомата представляет собой набор вершин, соответствующих различным состояниям автомата и соединяющих вершин дуг графа, соответствующих тем или иным переходам автомата. Если входной сигнал x_k вызывает переход из состояния z_i в состояние z_j, то на графе автомата дуга, соединяющая вершину z_i с вершиной z_j обозначается x_k. Для того, чтобы задать функцию переходов, дуги графа необходимо отметить соответствующими выходными сигналами. Для автоматов Мили эта разметка производиться так: если входной сигнал x_{k ­}действует на состояние z_i, то согласно сказанному получается дуга, исходящая из z_i­ и помеченная x_k; эту дугу дополнительно отмечают выходным сигналом y=(z_i, x_k). Для автомата Мура аналогичная разметка графа такова: если входной сигнал x_k, действуя на некоторое состояние автомата, вызывает переход в состояние z_j, то дугу, направленную в z_j и помеченную x_k, дополнительно отмечают выходным сигналом y=(z_j, x_k). При решении задач моделирования часто более удобной формой является матричное задание конечного автомата. При этом матрица соединений автомата есть квадратная матрица С=|| c_ij ||, строки которой соответствуют исходным состояниям, а столбцы - состояниям перехода. Элемент c_ij­­=x_k/y_S в случае автомата Мили соответствует входному сигналу x_k, вызывающему переход из состояния z_i в состояние z_j и выходному сигналу y_S, выдаваемому при этом переходе. Для F- автомата Мура элемент c_ij равен множеству входных сигналов на переходе (z_iz_j), а выход описывается вектором выходов: