4.Редуктор

4.1 Обоснование конструкции.

Редуктором называют зубчатый, червячный или зубчато-червячный передаточный механизм выполненный в закрытом корпусе и предназначенный для понижения угловой скорости, а следовательно повышения вращающего момента. Подобные механизмы, но используемые для повышения угловой скорости называются мультипликаторами. Редукторы условно делятся по различным признакам:  I По типу передачи редукторы могут быть зубчатые с простыми передачами (цилиндрическими, коническими, червячными), зубчатые, планетарные, волновые, и комбинированные. II В зависимости от числа пар звеньев в зацеплении редукторы бывают: 1) одноступенчатые 2) двухступенчатые  3) трехступенчатые  Редуктор состоит из литого чугунного (сварного стального) корпуса в котором смонтированы подшипниковые узлы служащие опорами для валов редуктора. Корпус закрыт крышкой. В верхней части крышки имеется закрываемое смотровой крышкой отверстие, предназначенное для осмотра внутренней части редуктора и заливки масла. По способу подвода смазочного материала к зацеплению различают картерное и циркуляционное смазывание. При сборке редуктора крышка прикрепляется к корпусу болтами. Размещение опор валов редуктора в жестком чугунном корпусе обеспечивает высокую точность зацепления зубчатых и червячных передач. Для защиты подшипников от попадания пыли и грязи, а так же для предупреждения утечки смазки из корпуса редуктора применяют уплотнение подшипниковых узлов. В нашем случае редуктор одноступенчатый, зубчатый, корпус чугунный.

2. Расчет передачи.

Исходные данные:

-угловая скорость быстроходного вала редуктора

ω₁=76,405 рад/с.

-угловая скорость тихоходного вала редуктора

ω₂=19.101 рад/с.

-крутящий момент быстроходного вала редуктора

Т₁=122 Н*м.

-крутящий момент тихоходного вала редуктора

Т₂=468 Н*м.

-передаточное отношение цилиндрической зубчатой передачи

U=4.

Для изготовления зубчатых колес используем сталь 40Х с последующей закалкой токами высокой частоты до твердости 400 НВ.

Эквивалентное число циклов перемен напряжений зубьев в зоне контакта.

Для шестерни:

N_HE1=(Т_max/Т_Н)³∙N_C1+(Т_Н/Т_Н)³∙N_C2+(Т_min/Т_Н)³∙N_C3, (4.1)

где Т_max – максимальный крутящий момент быстроходного вала, кН∙м;

Т_Н – номинальный крутящий момент быстроходного вала, кН∙м;

Т_min – минимальный крутящий момент быстроходного вала, кН∙м;

N_C1 – число циклов максимального момента быстроходного вала;

N_C2 - число циклов номинального момента быстроходного вала;

N_C3 - число циклов минимального момента быстроходного вала

N_HE1=(0.183/0.112)³*2.567*10⁶+(0.122/0.122)³*513.442*10⁶+ +(0.0366/0.112)³*342.29*10⁶=522.68*10⁶

для зубчатого колеса

N_HE2 = N_HE1/U (4.2)

N_HE2 =522.68*10⁶/4 =130‧10⁶ .

Базовое число циклов перемен напряжений в зубьях в зоне контактов

N_HОi=30H^2.4 _HB (4.3)

где H _HB твердость зубьев по Бриннелю

N_HО=30‧400^2,4=52,73‧10⁶

Коэффициент долговечности

K_HL= (4.4)

Если N_HE≥ N_HO то K_HL=1

N_HE1≥N_HO то K_HL1=1

N_HE2≥N_HO то K_HL2=1

Предел выносливости по контактным напряжениям

δ_Hlimb=17H_HRC+200 (4.5)

где H_HRC-твердость по Максвеллу

δ_Hlimb=17‧43+200=931 МПа.

Коэффициент запаса прочности

[S_H]=1,2 (поверхностная закалка)

Допускаемые контактные напряжения

[δ_H]= (4.6)

[δ_H1]=931‧1/1,2=775,8 МПа

[δ_H1]=[δ_H2]

[δ_H]= [δ_H]_min=775,8 МПа.

Коэффициент учитывающий неравномерность распределения нагрузки по ширине зубчатого венца

K_HB=1,15.

Коэффициент ширины венца

Ψ_bd=0,9‧0,9=0,81.

Коэффициент учитывающий динамическую нагрузку

K_HV=1,1.

Определяем межосевое расстояние

a_w=K_a(U+1)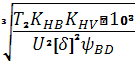 (4.7)

где K_a=495

Т₂-крутящий момент тихоходного вала редуктора.

U-передаточное отношение зубчатой передачи

a_w=495(4+1) ‧ =104,7 мм.

Принимаем стандартное межосевое расстояние а_w=125 мм

Номинальный модуль зацепления

m_n=(0,01…0,02)a_w=1,25…2,5 (4.8)

Примем стандартный модуль m_n=2.5

Число зубьев шестерни

Z₁=2 a_w/ m_n(U+1) (4.9)

где a_w -стандартное межосевое расстояние

Z₁=2‧125/2.5‧5=20

Принимаем Z₁=20

Число зубьев зубчатого колеса

Z₂=Z₁U (4.10)

Z₂=20‧4=80

Диаметры делительных окружностей шестерней колеса

d_i=m_nZ_i (4.11)

d₁=2.5‧20=50 мм

d₂=2.5‧80=200 мм

Диаметры вершин зубчатых колес

d_ai=d_i+2m_n (4.12)

d_a1=50+2.5‧1=55 мм

d_a2=200+2.5‧1=205 мм

Диаметры впадин шестерней колеса

d_fi=d_i-2,5m_n (4.13)

d_f1=50-2,5‧2.5=44 мм

d_f2=200-2,5‧2.5=194 мм

Ширина шестерни

b₁≥d₁‧ψ_bd (4.14)

b₁=50‧0,81=40,5 мм

применяем b₁= 45 мм

Ширина колеса

b₂=b₁-2 (4.15)

b₂=45-2=43 мм

Коэффициент ширины шестерни по межосевому расстоянию

ψ_BA=b₂/a_w (4.16)

ψ_BA=43/125=0.34

Окружная скорость колес и степень точности передачи

V_i= (4.17)

где ω-угловая скорость

d-диаметр делительной окружности.

V=76.405*50/2=1910.1 м/c

Для прямозубых колес при V до 5 м/с следует назначить 8-ю степень точности

Коэффициент нагрузки

K_H=K_Hβ+K_Hα+K_HV (4.18)

K_H=1,15‧1‧1,1=1,32

Проверка контактных напряжений

δ_Н=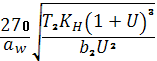 ≤ [δ_H] (4.19)

δ_Н=270/125‧ =723.6 МПа

723.6 ≤ 775,8

Силы, действующие в зацеплении:

Окружная сила

F_t=2T₁/d₁ (4.20)

Где T₁-крутящий момент быстроходного вала

d₁ - диаметр быстроходного вала.

F_t=2‧468000/50=18720 Н

Радиальная сила

F_r=F_t tgα/cosβ (4.21)

F_r=18720‧tg0/cos0 =6739.2 H

Осевая сила

F_a=F_t‧tgβ (4.22)

F_a=18720‧tg0=0 Н.

Проверяем зубья на выносливость по напряжениям изгиба

δ_F=F_t‧K_Fβ‧K_FV‧Y_F‧Y_β‧ K_FL/b_n‧m_n ≤ [δ_F] (4.23)

где F_t - окружная сила, 0;

K_Fβ= -коэффициент учитывающий неравномерность нагрузки по длине зуба_, K_Fβ=1,13;

K_FV – коэфицент учитывающий динамические действия напряжений, K_FV=1.2;

Y_F– коэфицент учитывающий форму зуба, Y_F1=3.75(шестерня);Y_F2=3.6(колесо);

Y_β–коэфицент учитывающий угол наклона зубьев;

K_FL–прочность зубьев;

b – ширина колеса, мм;

m_n– стандартный модуль, m_n=2мм.

Допускаемое напряжение

[δ_F] =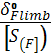 (4.24)

где δ_Flimb - предел выносливости при эквивалентном числе δ_Flimb=700 МПа

[S_F] –коэффициент безопасности

[S_F]=[S_F]^’‧[S_F]”

[S_F]^’=1,75 [S_F]”=1

[S_F] =1,75‧1=1,75

Допускаемые напряжения для для шестерни:

[δ_F1] =700/1,75=400 МПа

для колеса:

[δ_F2] =700/1,75=400 МПа

Находим отношение

[δ_F2]/Y_Fi (4.25)

для шестерни: 400/3.75=106.67 МПа

для колеса: 400/3.6=111.11 МПа

Определяем коэффициенты Y_β и K_FL

Y_β =1 – β/140 (4.26)

где - угол наклона зубьев β =0

Y_β =1 – 0/140=1

Проверку на прочность зубьев проводим по меньшему значению отношения [δ_F2]/Y_Fi

K_FL=4+ (ε_L-1)(n-5)/4* ε_L=0.92

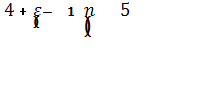где ε_L–коэфицент торцевого перекрытия ε_L=1,5

n- класс точности n=8

Проверяем прочность зуба колеса

δ_F=F_t‧K_Fβ‧K_FV‧Y_F‧Y_β‧ K_FL/b_n‧m_n ≤ [δ_F]

δ_F=18720‧1.13‧1.2‧3.75‧1‧0.92/43‧2.5=200.17 МПа

δ_F ≤ [δ_F]

200,17 ≤ 400

Условие выполнено.