5. Определение массы кристаллов.

1. Вывод правила рычага.

Массу кристаллов, выделившихся из расплава при его охлаждении, можно определить, используя правило рычага. Вывод этого правила приводим для точки О. Для этого составляем уравнение материального баланса по компоненту В при постоянной температуре.

m φ_B(O) = m_{раствора} φ_B(L)+m_{кристаллов} φ_B(K) (5.1)

m = m_{раствора} + m_{кристаллов} (5.2)

Подставив уравнение (5.2) в уравнение (5.1), получаем

(m_{раствора} + m_{кристаллов} ) φ_B(O) = m_{раствора} φ_B(L)+m_{кристаллов} φ_B(K) (5.3)

Решаем последнее уравнение относительно массы кристаллов:

m_{раствора} φ_B(O) + m_{кристаллов} φ_B(O) = m_{раствора} φ_B(L)+m_{кристаллов} φ_B(K)

m_{кристаллов}[φ_B(K) - φ_B(O)] = m_{раствора}[φ_B(O) - φ_B(L)] (5.4)

Из получившегося уравнения составляем пропорцию:

_{= ;}

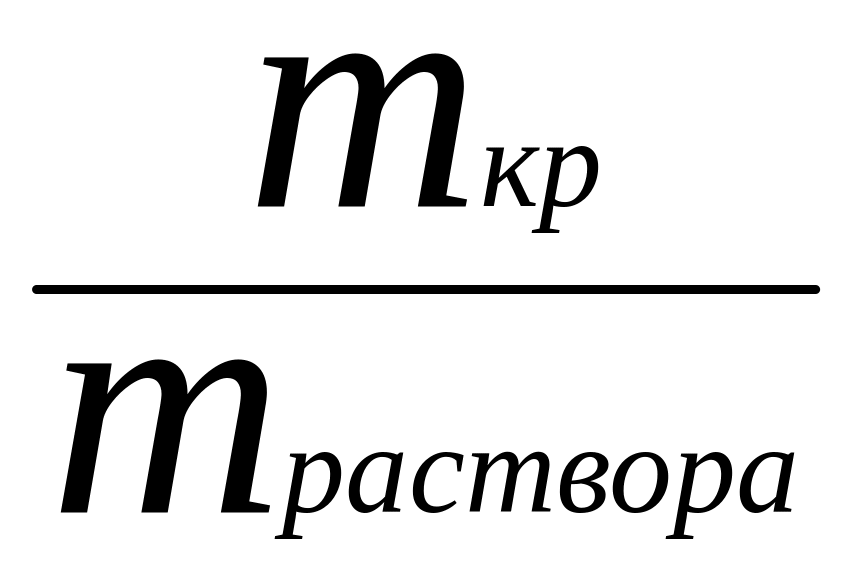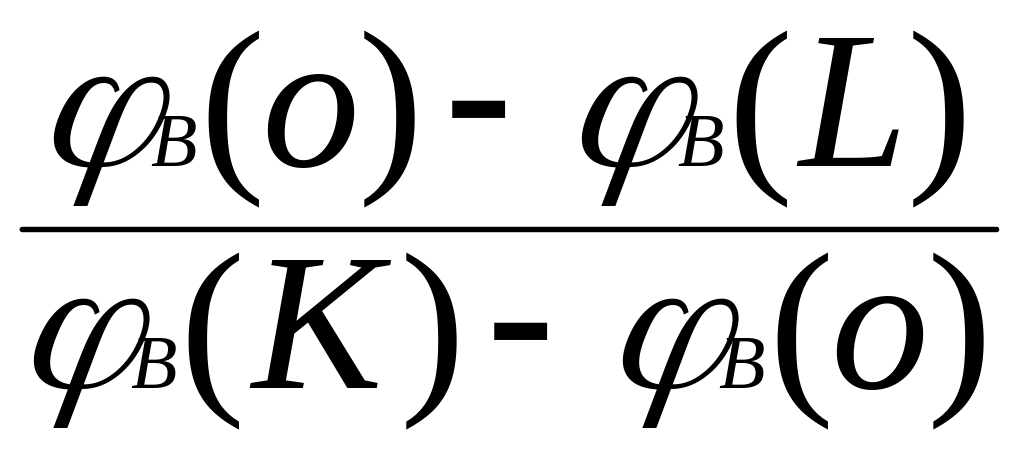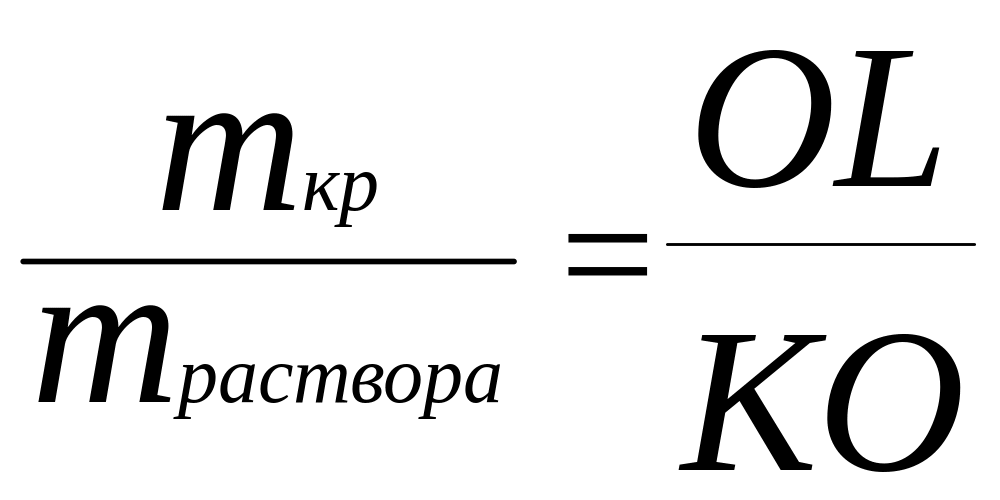(5.5)

2. Расчет.

Для точки О:

КО=20, OL=45, mраствора=2-mкр

mкр=2LO/(LO+OK)

mкр=1,38 кг

Для точки О':

К'О'=10 O'L'=17

mкр=2L’O’/(L’O’+O’K’)

mкр=1,25 кг

6. Уравнение шредера.

6.1. Вывод уравнения.

Рассмотрим равновесную систему, состоящую из двух фаз – жидкой и твердой. Пусть каждая фаза представляет реальный раствор. При фазовом равновесии

Т^ж = Т^тв = Т; р^ж = р^тв = р; µ_k^ж = µ_k^тв.

Химический потенциал компонента в каждой фазе зависит от температуры, давления и активности компонента

µ_k^ж = µ_k ^0,ж(T,p) + RTlna_k^ж; (6.1)

µ_k^тв = µ_k ^0,тв(T,p) + RTlna_k^тв; (6.2)

Где µ_k ^0,ж(T,p) и µ_k ^0,тв(T,p) – химические потенциалы чистого компонента в жидком и твердом состояниях при заданных температуре и давлении;

а_k^ж и а_k^тв – активности компонентов в равновесных фазах.

Учитывая (6.1) и (6.2), уравнение (4.1) можно преобразовать к виду

(6.3)

При постоянных температуре и давлении

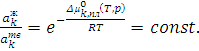(6.4)

Из (6.4) следует, что отношение активностей компонентов в равновесных фазах при постоянных температурах и давлении – закон фазового равновесия.

Если при заданных температуре и давлении добавить в одну из фаз некоторое количество компонента k, то это вызовет его перераспределение между фазами таким образом, что отношение активностей компонентов при вновь установившемся равновесии сохранится прежним. При изменении температуры или давления система перейдет в другое равновесное состояние, в котором изменится отношение активностей компонента в равновесных фазах и произойдет смещение равновесия.

Рассмотрим, как изменение температуры при постоянном давлении влияет на изменение состава равновесных фаз. Для этого выразим в уравнении (6.3) активности через мольные доли

(6.5)

Полученное уравнение продифференцируем по температуре

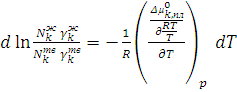(6.6)

Согласно уравнению Гиббса-Гельмгольца

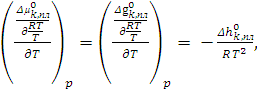(6.7)

где – изменение химического потенциала чистого компонента при переходе из твердого состояния в жидкое;

– мольная теплота плавления компонента.

Использовав уравнение (6.7), получим

. (6.8)

Последнее уравнение в дифференциальном виде описывает влияние температуры на состав равновесных фаз при изобарном смещении равновесия, при переходе из равновесного состояния при одной температуре в равновесное состояние при другой температуре.

Твердые растворы образуют компоненты, близкие по химическим и физическим свойствам и имеющим одинаковый тип кристаллической решетки. Если компоненты в твердой фазе не растворимы друг в друге, то из жидкого раствора выделяются кристаллы чистого вещества. В этом случае имеет место равновесие: жидкий двухкомпонентный раствор и кристаллы одного из компонентов (N_k^тв =1, γ_k^тв =1), а уравнение принимает вид

(6.9)

Проинтегрируем это уравнение, допустив, что не зависит от температуры

(6.10)

Здесь и – температуры кристаллизации чистого компонента из раствора и температура кристаллизации чистого вещества. Уравнение (6.10) в интегральной форме описывает влияние температуры на равновесие «жидкий раствор – кристаллы компонента». Если жидкая фаза близка по свойствам к идеальному раствору (γ_k^ж =1), то уравнение (6.10) записывается в виде

(6.11)

Последнее уравнение носит название уравнения Шредера, в котором – мольная доля компонента в жидком растворе, находящемся в уравнении с его кристаллами, то есть концентрация компонента в насыщенном растворе или растворимость компонента k при температуре

Из уравнения Шредера следует, что в случае идеальных растворов растворимость компонентов возрастает с увеличением температуры.